OR学会機関誌「オペレーションズ・リサーチ」2024年4月号の特集「エンジニアリングのためのゲーム理論」に「ゲーム理論のトリセツ」という記事を書きました。
また、Chat GPTを使いながら私が編集した小島武仁先生の講演録「社会の「ゲームのルール」を科学する―マーケットデザインの理論と実践―」も掲載されています。(1年間は学会員限定です)

Navigator to Game Theory
OR学会機関誌「オペレーションズ・リサーチ」2024年4月号の特集「エンジニアリングのためのゲーム理論」に「ゲーム理論のトリセツ」という記事を書きました。
また、Chat GPTを使いながら私が編集した小島武仁先生の講演録「社会の「ゲームのルール」を科学する―マーケットデザインの理論と実践―」も掲載されています。(1年間は学会員限定です)
昨年(2021年)の10月に東京都立大学のオープンユニバーシティで講義した「高校生のためのゲーム理論入門」(高校生のための大学授業体験シリーズ)の動画が、東京都立大学のホームページ内でOCWとして公開されることになりました!
2021年度東京都立大学オープンユニバーシティ・高校生のための大学授業体験シリーズ 高校生のためのゲーム理論入門
他のゲーム理論講義動画とともにどうぞ
部分ゲーム完全均衡について、ざっくりと説明します。
部分ゲーム完全均衡(Subgame Perfect Equilibrium, SPE)とは「ある点から後がゲーム(部分ゲーム)とみなせるときには、プレイヤーはそのゲームのナッシュ均衡を選んでいる」と考えるゲームの解です。
次のようなゲームを考えてみましょう。
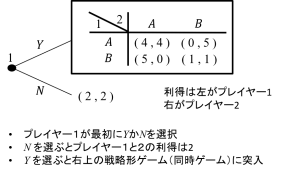
このゲームは最初にプレイヤー1がYかNかを選択。Nを選べば右上の戦略形ゲーム(同時ゲーム)に突入し、Nを選べばゲームは終了してプレイヤー1と2の利得が共に2となるゲームです。
このゲームの解はどうなると予想されるでしょう?プレイヤー1は最初の点で、Yを選んだときに、その結果がどうなるかを予想しなければなりません。右上の戦略形ゲームでは、ナッシュ均衡は(B,B)なので、プレイヤー1の利得は1になると予想されます。

このことからプレイヤー1は最初の点でYを選べば利得は1、Nを選べば利得は2になるのでNを選ぶと考えられます。部分ゲーム完全均衡は「プレイヤー1は最初の点でYを選び、次の戦略形ゲームでプレイヤー1と2は共にBを選ぶ」となります。

部分ゲーム完全均衡を正確に学ぶためには、(1)展開形ゲームはどのように書けて、それを戦略形ゲームに変換するにはどうするのか、(2)展開形ゲームにおいて、ある点から後をゲーム(部分ゲーム)とみなせるのはどういうときか、を学ぶ必要があります。それはまた今度にします。今はこちらの動画を参考にしてください。
部分ゲーム完全均衡はナッシュ均衡の1つ(精緻化されたもの)です。例を使って、(ボンヤリとですが)説明してみましょう。
次のゲームを考えます。
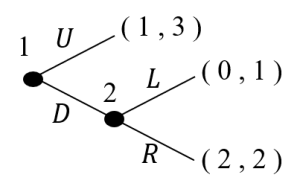
このゲームは、プレイヤー1がUかDを選び、プレイヤー2がLかRを選ぶ戦略形ゲーム(同時のゲーム)と考えることもできます。

ここで「交互にプレイする展開形ゲームを、同時にプレイする戦略形ゲームに変換できるのか?」という疑問があるかと思います。確かにそこが最大のポイントですね。確かにプレイヤー2は、プレイヤー1がDを選んだのを知ってから、LかRを選ぶわけです。しかし、プレイヤー2はゲームが始まる前に「もしプレイヤー1がDを選んだらどうするか」を決めておくことはできるはずです。またプレイヤー1は、「もしDを選んだらプレイヤー2はどうするか」を推測しなければ自分の選択を決めることができません。プレイヤー1の頭の中では、プレイヤー2がどうするかは、自分が選択をする前(ゲームが始まる前)に決まっていなければなりません。このように展開形ゲームでは「すべてのプレイが行われる前に、各プレイヤーはどの点で何が選ばれるかを決定しておく」として、戦略形ゲームとして考えることができるわけです。
この戦略形ゲームのナッシュ均衡は(U,L)と(D,R)の2つです。
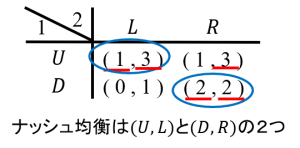
一方、このゲームの部分ゲーム完全均衡はどうなるでしょう。プレイヤー2が行動する点は部分ゲームと考えることができます。プレイヤー2はLを選べば利得1、Rを選べば利得2ですからRを選びます。このプレイヤー2の行動を推測すると、プレイヤー1はDを選びます。

ナッシュ均衡がすべて、部分ゲーム完全均衡になるわけではありません。ここで、部分ゲーム完全均衡ではない(U,L)というナッシュ均衡が、どういうものかを考えてみましょう。図では以下のようになりますね。

このナッシュ均衡では、各プレイヤーが(U,L)が起こると予想しています。プレイヤー2は、プレイヤー1がUを選ぶと予想すれば、Lを選んでもRを選んでも利得は同じなので、Lを選んでも悪くはありません。そして、プレイヤー1は、プレイヤー2がLを選ぶと予想すれば、Uを選ぶことが最適です。したがって、この戦略の組は「すべてのプレイヤーにとって、相手がその戦略を選ぶならば、自分にとって最適な戦略を選んでいる」ようなナッシュ均衡になるのです。
確かにプレイヤー2は「プレイヤー1がUを選んだと予想したときは、Lを選んでもRを選んでも利得は同じ」です。しかし、このゲームは同時のゲームではありません。予想ではなく、実際にプレイヤー1がDを選んだ場合には、プレイヤー2は、もはやLを選ばずRを選ぶでしょう。
このように展開形ゲームを戦略形ゲームに変換すると、「プレイヤーが選択した行動の情報」を考慮せずに、プレイヤーの推測を考えることになってしまうように見えます(そう見えますが、本当にそうかどうかは、難しいところです)。
そのため、変換した戦略形ゲームのナッシュ均衡をそのまま解として考えると不完全で、展開形ゲームの構造を考慮して、ナッシュ均衡の中から適切でない解を除く必要があります。これを均衡の精緻化(equilibrium refinement)と呼びます。部分ゲーム完全均衡はナッシュ均衡の精緻化による解の1つです。
完全情報展開形ゲームとその解き方であるバックワードインダクション(backward induction)について「展開形ゲームとは?ゲームの木とは?」で、ざっくりと話しました。ここではバックワードインダクションによるゲームの解き方を、もう少し詳しく説明します。
バックワードインダクションは完全情報展開形ゲームの解き方です。各プレイヤーは自分よりあとに行動するプレイヤーの行動を先読みし、自分の利得を最大にするように行動を選ぶのでした。
これを言い換えるとゲームは「時間的に後から行動するプレイヤーの行動から順番に解いてゆく」ということになります(有限時間の場合)。後から帰納的に(順番に)解くという意味でバックワードインダクションと呼ばれるのです。
バックワードインダクション(backward induction)は翻訳すると「後向き帰納法」「後向き遡及法」などと翻訳されるのですが、しっくりこないんでカタカナ語で書いたりすることが多いです。
具体的には、次のようにゲームを解いていきます。
1。最後のプレイヤー、つまり「そのプレイヤーが何を選んでもゲームが終わる」ようなプレイヤーの行動を求めます。そのプレイヤーは、自分が行動を選ぶと自分の利得が決まるので、そのプレイヤーが自分の利得を最大にする行動を決定することができます。
2。既に行動を求めたプレイヤーの直前に行動するプレイヤーの中から、<そのプレイヤー以降に行動するプレイヤーの行動がすべて決まっているプレイヤー>の行動を求めます。そのプレイヤーは、自分が行動を選ぶと、それ以降のプレイヤーの行動が決まっている(か、またはゲームが終わる)ために利得が決まるので、利得を最大にする行動を決定することができます。
3。2を繰り返して行き、一番最初のプレイヤーの行動が求められたら終わり…です。
いくつかの例題を見てみましょう。説明をするためには、ゲームの木の点に名前がついていると便利ですので、そうしておきます。(正確には意思決定点にラベルを付けておきます。ゲームの木を少し詳しく説明!も参照してください。)
(例1)まず最初は「展開形ゲームとは?ゲームの木とは?」で説明した<コンビニ立地ゲーム>の例(図1)を、バックワードインダクションの手順の観点から、もう一度解いてみます。
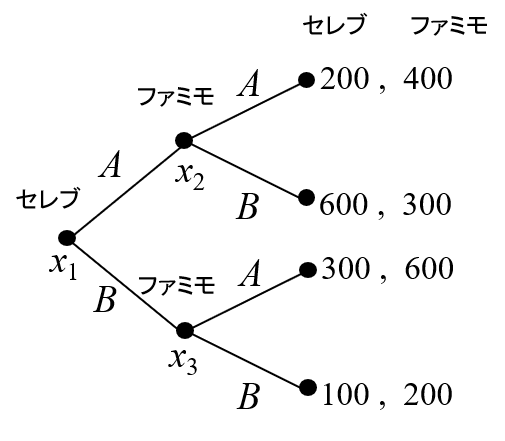
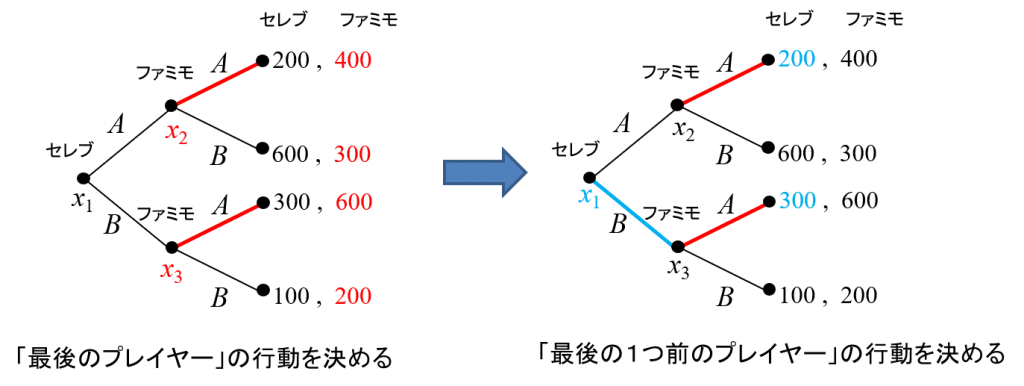
1。最後に行動するプレイヤーは、\(x2\),\(x3\)で行動するファミモなので、そこでの行動を決めます。 \(x_2\)では、ファミモはAを選べば利得が400、Bを選べば利得が300となのでAを選びます。 \(x_3\)では、ファミモはAを選べば利得が600、Bを選べば利得が200なのでAを選びます。こうして最後に行動するプレイヤーの行動が決まります。
2。次に、既に行動を求めたプレイヤーの直前に行動するプレイヤーは\(x_1\)で行動するセレブだけなので、そこでの行動を決めます。\(x_1\)では、セレブは、Aを選ぶと(ファミモがAを選ぶので)利得が200、Bを選ぶと(ファミモがAを選ぶので)利得が300となるのでBを選ぶ、というように行動が決定できます。これで最初のプレイヤーまで遡って行動が決まったので、おしまいです(図2)。
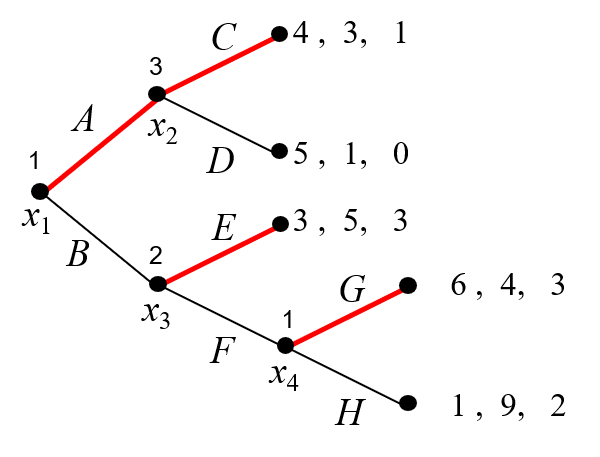
(例2)もう少し複雑な例を考えてみましょう(図3)。今度は3人のゲームです。
図3はプレイヤー1,2,3の3人からなる、以下のようなゲームです。

図3において、各点の上の数字は行動するプレイヤーを表しています。ゲームが終わったときの利得は、常に左からプレイヤー1、2、3の順になっています。
このゲームを、バックワードインダクションの手順に従い解いてみましょう。
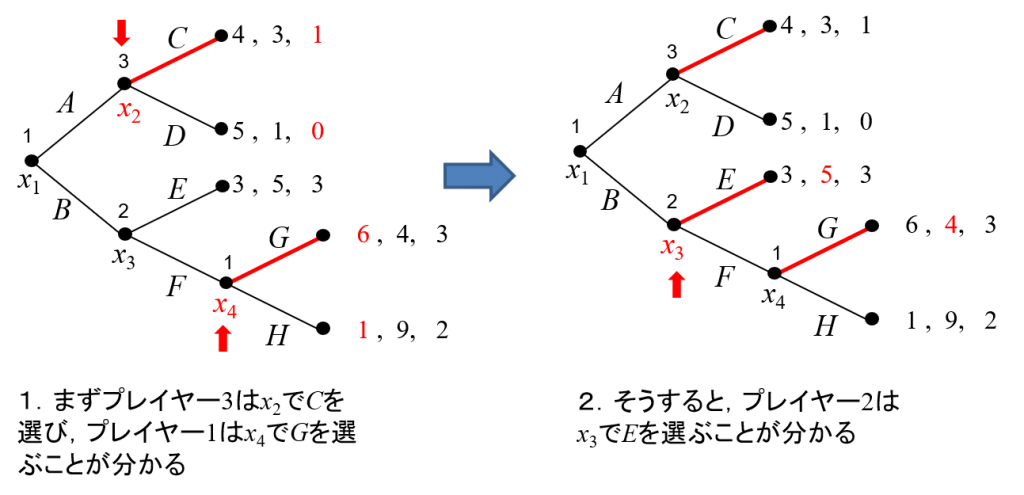
1。最後に行動するプレイヤー(そのプレイヤーが何を選んでもゲームが終了するプレイヤー)の行動です。このゲームでは\(x_2\)で行動するプレイヤー3と、\(x_4\)で行動するプレイヤー1なので、そこでの行動を決めます。 \(x_2\)では、プレイヤー3は\(C\)を選べば利得が1、\(D\)を選べば利得が0なので\(D\)を選びます。\(x_4\)ではプレイヤー1は\(G\)を選べば利得が6、\(H\)を選べば利得が1なので\(G\)を選びます。こうして最後に行動するプレイヤーの行動が決まります。
2。次に、<そのプレイヤー以降に行動するプレイヤーの行動がすべて決まっているプレイヤー>は、\(x_2\)で行動するプレイヤー2なので、そこでの行動を決めます。\(x_2\)でプレイヤー2は、\(E\)を選ぶと利得が5、\(F\)を選ぶと(プレイヤー1がGを選ぶので)利得が4、となるので\(E\)を選ぶ、ということになります。(図4)
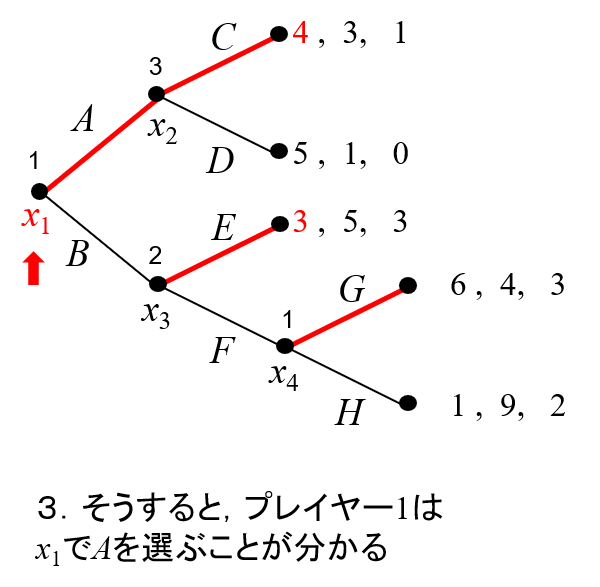
3。次に、\(x_1\)で行動するプレイヤー1の行動を決めます。\(x_1\)でプレイヤー1は、\(A\)を選ぶと(プレイヤー3が\(C\)を選ぶので) 利得が4、\(B\)を選ぶと(プレイヤー2が\(E\)を選ぶので)利得が3となるので\(E\)を選ぶ、ということになります。
以上、バックワードインダクションによる完全情報ゲームの解の求め方について解説しました。このときバックワードインダクションで得られるゲームの解と、それによって予測されるゲームの結果は何であるか、について区別しなければなりません。ここで
ゲームの解とは、すべての点で各プレイヤーが何を選ぶかを、すべて明らかにしていること
ゲームの結果とは、ゲームの解によって、最初(初期点)のプレイヤーから順番にどのような行動が選ばれゲームが進行して、どの点でゲームが終わるかを示したもの
です。
例えば最初の例1を見てみましょう(図6)。
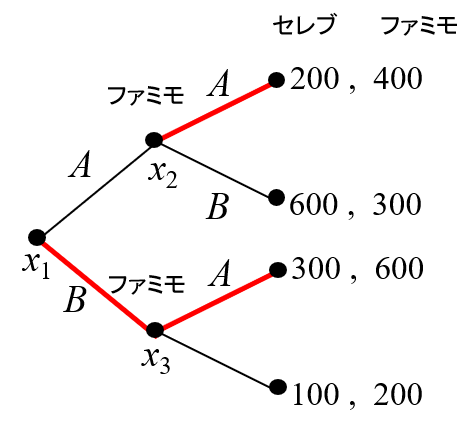
このときゲームの解は「 \(x_1\)でセレブがBを選び、\(x_2\)と\(x_3\)でファミモはAを選ぶ」となります。このようにゲームの解はすべての点でプレイヤーが何を選ぶかを定めたものです。
これに対し、\(x_1\)でセレブがBを選べば、次に\(x_3\)でファミモがAを選んでゲームは終わり、実際には\(x_2\) は実現しません。ゲームの解によって、実際に起きる結果は解の一部です。
「すべての点(正しくは意思決定点)で何が選ばれるか」が決まると、「最初のプレイヤー(初期点)から、順番にどのプレイヤーがどの行動を選んでゲームが進行して、最後のプレイヤーの行動が決まって利得が決まるところ(終点)」まで一本の経路(path)ができます。この経路は均衡経路(equilibrium path)と呼ばれます。この均衡経路はゲームの結果であると考えられます。 この例の場合、均衡経路(=ゲームの結果)は「 \(x_1\)でセレブがBを選び、\(x_3\)で、ファミモはAを選ぶ」となります。
「すべての意思決定点で何が選ばれるか」は「戦略の組(strategy profile)」に対応するものです。またこれは1つの経路を実現すると考えても良いし、1つの終点が決まると考えても良いです。なお途中で確率による選択(混合戦略)があると、経路は1つではなく、複数の経路が確率的に決定されると考えられます。
ゲームの解において、均衡経路ではない意思決定点は均衡外経路(off-equilibrium path)と呼ばれます。 例1では\(x_2\)は均衡外経路です。このことよりゲームの解が異なってもゲームの結果が同じになることがあることに注意しましょう。
例2で、ゲームの解とゲームの結果が何であるかを練習してみましょう。
この例2の場合は
となります。いかがでしょうか。
<後から解く>バックワードインダクションは、時間経過を伴う最適化問題である動的最適化(マクロ経済学、ファイナンス理論)、ネットワーク最適化問題にも用いられる一般的手法です。この概念を方程式に直すといわゆるベルマン方程式となります。
以下も参考にしてください。
ゲーム理論のゲームには、戦略形ゲーム(strategic form)と展開形ゲーム(extensive form)という2つの「表現」があります。戦略形ゲームは、プレイヤーは同時に行動を選ぶと考えてゲームを表します。これに対し、展開形ゲームは、先手と後手のあるゲームなど、どんなゲームでも表現できて、プレイヤーは同時に行動しなくても良いのです。
このような展開形ゲームの中でも、プレイヤーが1人ずつ順番に行動を選び(同時に行動することはなく)、各プレイヤーは自分より先に行動したプレイヤーが何を選んだかがすべて分かるゲームを完全情報(perfect information)の展開形ゲームと言います。代表的な例は、チェス、囲碁、将棋です。将棋で「自分より前に指した手が、何か分からん!」ってことはありませんよね?
完全情報ではないゲームは不完全情報(imperfect information)と呼びます、あたりまえですね。不完全情報ゲームの例としては、たとえば...「2人でじゃんけんをするとき、まず1人がグー・チョキ・パーを選んで紙に書いて相手に見えないように封筒に入れ、次にもう1人が改めてグー・チョキ・パーを選ぶ」という面倒なじゃんけんは不完全情報ゲームです.
...って、あれ?戦略形ゲームで勉強したように、これは同時に行動することと同じでした。「プレイヤーが同時に行動する戦略形ゲーム」は「不完全情報の展開形ゲーム」の典型的な例です。これはまた別の機会に。
ここでは完全情報の展開形ゲームとその解き方について学んで行きます。乱暴に言うと
ということになります。乱暴すぎてかなり間違ってますが、細かいことは気にせず、ざっくり説明します。正確な定義や説明はゲーム理論のテキストなど読んでください。
以下の例を考えましょう。戦略形ゲームの支配戦略やナッシュ均衡の説明で使った例と同じです。今度はプレイヤーは同時に行動を選ぶのではなく、セレブ、ファミモの順に選びます。
2つのコンビニ、セレブ(セレブイレブン)とファミモ(ファミリーモール)が、A駅とB駅のどちらか一方に出店しようと考えている。コンビニを1日に利用する客はA駅が600人、B駅が300人である。セレブとファミモが違う駅を選べば利用客を独占できる。しかし同じ駅に出店すると、ファミモが人気で、ファミモはセレブの2倍の客数を獲得できる。すなわち両方がA駅に出店すると、セレブ200人、ファミモ400人。B駅に出店すると、セレブ250人、ファミモ500人である。ここで客数を利得と考える。
ここでは、まずセレブが先にどちらの駅を選ぶかを決定し、ファミモはそれを知ってから自分がどちらの駅に出店するかを決める。セレブとファミモはどちらの駅に出店するだろうか?
戦略形ゲームのように同時に行動するのではなく、プレイヤーが順番に行動をするゲームが展開形ゲームです。展開形ゲームは次のようなゲームの木で表します。

ゲームの木の正確な定義は後でやろうと思いますが、ざっくりと理解したい人には、ゲームの木の説明は不要でしょう?まず最初にセレブがAかBかを選び、次にそれを知ってからファミモがAかBかを選ぶと、結果が決まるのでセレブとファミモの利得がそこに書いてある、とそんな感じです。
ではさっそく、このゲームを解いてみましょう。皆さんがセレブだったらAとBのどちらを選ぶでしょうか?セレブがAを選ぶと、うまく行けば(ファミモがBを選べば)600の利得を得られますし、Bを選ぶとヘタをすれば(ファミモがBを選べば)100の利得になってしまいますね。だから、セレブはAを選ぶことが答のように思えるかも知れません。
しかし、ゲーム理論の答ではセレブはBを選びます。
なぜでしょうか?このゲームでは、セレブだけではなく、相手プレイヤーのファミモも利得を大きくしたいと考えています。セレブは「うまく行けば」「ヘタをすると」と、自分勝手に考えるのではなく、ファミモの行動を考えて、自分の行動を選択する必要があります。このためにはセレブの次に行動するファミモの行動を先読みする必要があるわけです。
ファミモの行動を先読みしてゲームを解いてみましょう。
これを先読みするとセレブは、Aを選ぶと(ファミモがAを選ぶので)利得が200、Bを選ぶと(ファミモがAを選ぶので)利得が300となるのでBを選ぶ、ということになります(下図)。
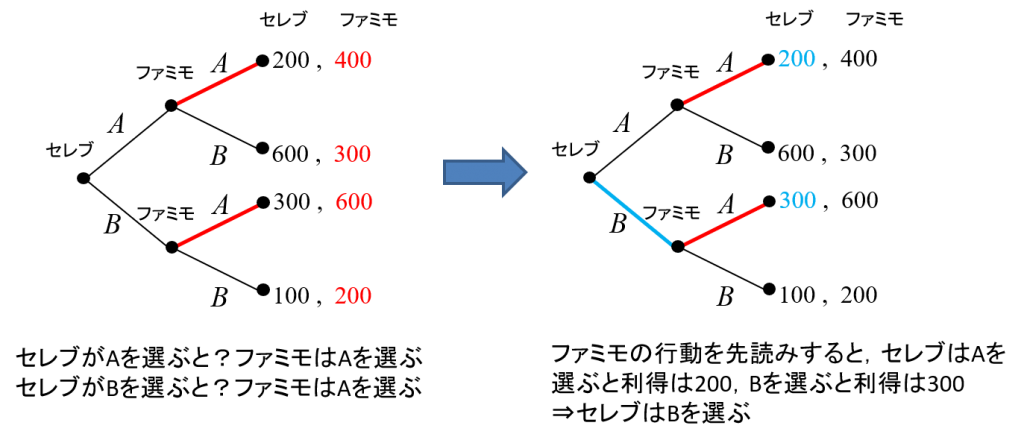
結果は「セレブがBを選び、ファミモがAを選ぶ」となります。これが(完全情報)展開形ゲームの解き方です。この先読みによるゲームの解き方はバックワードインダクションと呼ばれます。
以上、とりあえず完全情報展開形ゲームについての簡単な説明と解き方でした。乱暴に言うと
ということでしたね。乱暴すぎて、かなり間違ってますが、最初は細かいことは気にせず、そんな感じで覚えておけばよいでしょう。正確な定義や説明はゲーム理論のテキストなど読んでくださいね。なお。
囚人のジレンマは、ゲーム理論の中で、もっとも有名な例・モデルと言えるでしょう。
2人のプレイヤーが「協力するか」「協力しないか」を選ぶ問題で、以下の3つの条件が成立するときに、それは囚人のジレンマと呼ばれます。
(1)各プレイヤーは、相手が協力するならば、自分は協力しないほうが良い。
(2)各プレイヤーは、相手が協力しなくても、自分は協力しないほうが良い。
(3)しかし各プレイヤーは、2人が協力しないよりは、2人が協力したほうが良い。
(1)と(2)から、相手が何を選んでも自分は「協力する」より「協力しない」ほうが良いので、2人は協力しないことを選択します。しかしその結果が2人が協力することよりも悪くなっているために問題となるわけです。
ここで 「協力する」ことはゲーム理論では支配戦略と呼ばれます。支配戦略は、相手が何を選んでも、自分にとって他の選択より良い選択です。このことから支配戦略を選ぶことは自明のように思えるのですが、 囚人のジレンマを考えると支配戦略を選ぶことが必ずしも自明では思えなくなります。
この問題が囚人のジレンマと呼ばれるのは、タッカー(A. Tucker。カルーッシュ・クーン・タッカー条件(Karush-Kuhn-Tucker condition)のタッカーです)という数学者が上の状況を以下のようなストーリーで表現したことが由来であると言われています(以下はタッカーのオリジナルのストーリーとは違います)。
(囚人ジレンマ ストーリー)重罪を犯しているが、証拠が不十分なため軽微な罪で逮捕されている2人の囚人がいる。彼らは別々な部屋で取引を持ちかけられる「お前だけが重罪について自白すれば無罪にしてやる」。
もし2人が黙秘を続けると、軽微な罪で懲役1年である。しかし1人が自白し、1人が黙秘をすると、自白した方は釈放、黙秘した方は(捜査に協力しないことで罪が重くなり)懲役10年。しかし両方が自白すると(重罪で)懲役5年になる。
さて、あなたが囚人ならば自白したほうが良いか、黙秘したほうが良いか?
この状況を表にすると、以下のようになります。
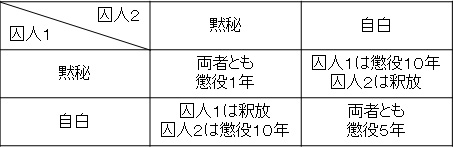
先に述べた「協力すること」を「黙秘」に、「協力しないこと」を「自白」に置き換えると、囚人のジレンマの3条件に当てはまることが分かります。すなわち、
(1)各囚人は、相手が黙秘するなら、自分は自白するほうが良い。
(2)各囚人は、相手が自白するとしても、自分は自白するほうが良い。
(3)しかし各囚人は、2人が自白するよりは、2人が黙秘したほうが良い。
相手が黙秘しても自白しても、自分は黙秘するより自白するほうが良いので、2人は自白を選びます。しかし、その結果は2人が黙秘するよりも悪くなります。
この問題が興味を持たれるのは、社会や経済や政治の問題にこのジレンマが多く現れるからです。例えば
と言った現象です。なお安売りの問題は、安売りをしている企業にとっては問題ですが、消費者にとってはそれ以上に恩恵があります。市場の価格競争は、囚人のジレンマという構造を利用して消費者の厚生を高める仕組みだと言うこともできます。
囚人のジレンマは、本来なら協力することが望ましい2人が協力しない方が良いという結果になってしまうジレンマです。これは、協力することをコミットするような契約(協力しなければ罰金を払うなど)を結ぶことで解決できる可能性がありますが、国家間の関係のように、このような契約を結ぶことが難しい場合もあります。このような場合、囚人のジレンマの状況は1回きりではなく、長期間に継続する問題でもあります。このような長期間に続く囚人のジレンマは、囚人のジレンマを何度も繰り返すようなゲームだと考え、繰り返しゲームという枠組みで分析されます。
囚人のジレンマを語るには、以下のことに注意する必要があります。
X先生と2人で教授会で口論になり、教授会の時間がどんどん長引いている。(1′)X先生が折れるなら、自分は折れるより折れないほうがいい。(2′)自分が折れるなら、X先生は折れるより折れないほうがいい。(3′)でも2人が折れないなら、教授会は長引くばかりで、それなら2人とも折れたほうがいい(まったくの、まったくのフィクションです)。一見すると条件が3つ揃ってるように見えますが、(1′)も(2′)も「相手が協力するなら、自分は協力しないほうが良い」という囚人のジレンマの条件(1)を2人のプレイヤーに分解して言い換えただけで、条件(2)(相手が折れないなら、自分は折れたほうが良いのか、折れないほうが良いのか)が特定されていません。もし「相手が折れないなら、自分は折れたほうがいい」ならば、これはチキンゲームです。
戦略形ゲームにおいては、各プレイヤーがどの戦略(選択、行動、代替案)を選ぶかを決めることが分析の主たる目的となります。
このとき1人のプレイヤーに対して
自分以外のプレイヤーが何を選んでも、自分の他の戦略よりも良い戦略(利得を高くする戦略)
があれば、その戦略を(そのプレイヤーの)支配戦略と呼びます。
プレイヤーに支配戦略があれば、そのプレイヤーはその支配戦略を選ぶと考えます。
例を挙げましょう。
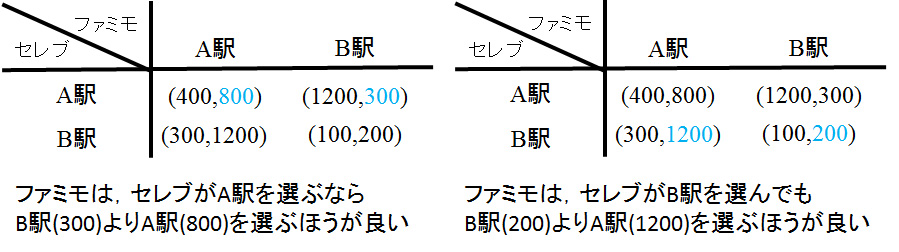
支配戦略の例(コンビニ戦争2):2つのコンビニ、セレブ(セレブイレブン)とファミモ(ファミリーモール)が、まだコンビニがないA駅とB駅のどちらか一方に出店しようと考えている。コンビニを1日に利用する客はA駅が1200人、B駅が300人である。セレブとファミモがもし違う駅を選べば、利用客を独占できる。しかし同じ駅に出店すると、ファミモが人気で、ファミモはセレブの2倍の客数を獲得できる。すなわち両方がA駅に出店すると、セレブ400人、ファミモ800人。B駅に出店すると、セレブ100人、ファミモ200人である。ここで客数を利得と考える。セレブとファミモはどちらの駅に出店するだろうか?
ゲーム理論を持ち出すまでもなく、ちょっと考えるとセレブもファミモもA駅を選ぶことが分かるでしょう。B駅を独占しても高々300人ですからね。でも最初はこの例から始めましょう。
このゲームを利得行列で書くと下のようになります。

このときセレブの視点に立ってみましょう。セレブは
と言うことが分かります。セレブは、ファミモが何を選んでも、B駅よりはA駅の方が良い戦略です。したがってA駅はセレブの支配戦略です(以下の図)。
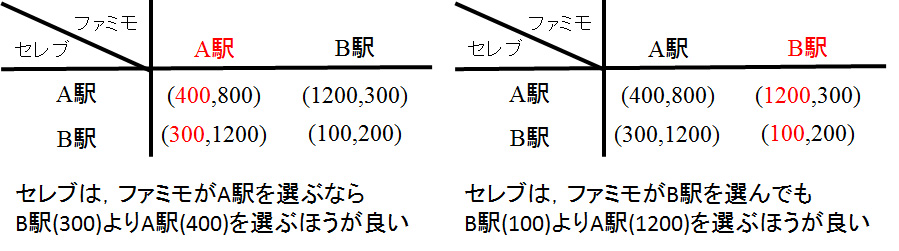
同様に ファミモの視点に立って考えてみます。
セレブは、ファミモが何を選んでも、B駅よりはA駅の方が良い戦略です。したがってA駅はセレブの支配戦略です。
もしすべてのプレイヤーに支配戦略があれば、すべてのプレイヤーが支配戦略を選ぶことがゲームの答となり、そのゲームは解けたことになると言えるでしょう。今回の例では、セレブもファミモも支配戦略はA駅でしたから、両方ともA駅を選ぶと予測でき、ゲームは解けたことになります。
支配戦略は、相手の選択に関わらず、自分にとって他の選択より良いような選択がある場合です。このときプレイヤーは、相手や自分にとっての知識が完全でなくても行動を確定することができます。例えば、
(禅が好きなアリス)アリスと文太は、それぞれ禅寺に行くか、ショッピングセンターに行くか悩んでいる。アリスはとにかく禅寺に行きたいので、文太が禅寺に行っても行かなくても、ショッピングセンターよりは禅寺がいい。
この場合、アリスにとって禅寺に行くことが支配戦略になり、アリスは禅寺に行くことが確定します(だから「悩んでいる」って問題設定はおかしいんだけど)。しかも
ということになります。つまり支配戦略があれば、細かい情報はなくてもプレイヤーはそれを選ぶことになります。このことは、支配戦略によるプレイヤーの行動の予測は、かなり確かなものになっているということで、支配戦略がないゲーム(その解はナッシュ均衡)よりも、より確からしい予測を与えているということになります。
このように支配戦略があればゲームの解は自明なように思えますが、必ずしもそうではないように見えるゲームがあります。それが囚人のジレンマであり、共有地の悲劇です。
戦略形ゲームは、展開形ゲームと並ぶ非協力ゲームの表現形式です(参照:戦略形ゲームと展開形ゲーム)。戦略形ゲームは、プレイヤー、戦略、利得の3つの要素から構成されます。すべてのプレイヤーは同時に戦略を選び、その結果、各プレイヤーの利得が決まります。
戦略形ゲームの例として、次のような問題を考えてみましょう。
戦略形ゲームの例(コンビニ戦争1):2つのコンビニ、セレブ(セレブイレブン)とファミモ(ファミリーモール)が、まだコンビニがないA駅とB駅のどちらか一方に出店しようと考えている。コンビニを1日に利用する客はA駅が600人、B駅が300人である。セレブとファミモがもし違う駅を選べば、利用客を独占できる。しかし同じ駅に出店すると、ファミモが人気で、ファミモはセレブの2倍の客数を獲得できる。すなわち両方がA駅に出店すると、セレブ200人、ファミモ400人。B駅に出店すると、セレブ100人、ファミモ200人である。ここで客数を利得と考える。セレブとファミモはどちらの駅に出店するだろうか?
本題に入る前に言っておきたいのですが、別にこのページはコンビニの戦略の話をしたいのではなくて、ゲーム理論とは何かを話すための「例」ですからね。「両方に出店するというのはないのでしょうか」とか聞く人がいるけど(本当にたくさんいる)、そうしたければ、そういう例を勝手に考えてください。むかし、あるビジネス系の雑誌に、こういう例を出したら、雑誌の編集部の人がコンビニの会社の人に聞きに行って、そしたら「うちには『客を取り合う』という発想はない。2つのコンビニに同じ駅に出店すると集積効果があって、利用客は増える」とか言われてしまったのですが、そうならば、そういう例を作ればいいですよ。でも増えたりしたら、例として分かりにくいじゃないですか。ここはリアリティを求めてるんじゃなくて、わかりやすい例にしてるんです。
で、本題です。上記の例の場合、戦略形ゲームの3要素(プレイヤー、戦略、利得)は
のようになります。このようにプレイヤーが2人のゲームを2人ゲームと呼び、その中でも両プレイヤーの戦略の数が2つの場合は2✕2ゲーム(ツーバイツーゲーム、と呼ぶ)と呼ばれます。2✕2ゲームは、戦略形ゲームの中で最も簡単なゲームであると言えます。
「利得は上記に書かれている」と言われても見にくいので、このような2人戦略形ゲームを表すには、以下のような利得行列という表を使います。

この表では、セレブが行(水平方向)を選択し、ファミモが列(垂直方向)を選択し、交わったセルの左側の数値がセレブの利得、右側の数値がファミモの利得を表します。例えば、セレブがA駅、ファミモがB駅を選ぶと…
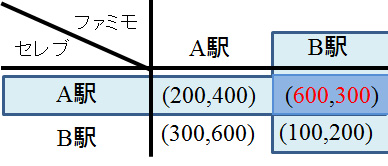
このようになり、セレブの利得が600、ファミモの利得が300になることが分かります。
利得行列にはいろいろな書き方があり、下の図のようにセルを左下と右上に区切り、左下に第1プレイヤー(行を選ぶプレイヤー、今回はセレブ)の利得、右上に第2プレイヤーの利得を書く場合もあります。
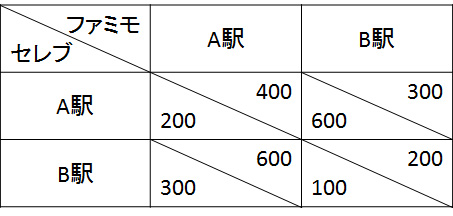
戦略形ゲームにおいて、「プレイヤーが選ぶ戦略の組合せはどこになるのか」を求めることをゲームを解くと呼びます。ゲームを解くポイントは、支配戦略とナッシュ均衡です。
ものすごく乱暴に言うと「ゲーム理論(非協力ゲーム)には、戦略形ゲームと展開形ゲームがあり、戦略形ゲームは利得行列で表し、展開形ゲームはゲームの木で表す」ということになります。乱暴すぎて、かなり間違ってますが、最初から細かいことは覚えられないので、ざっくりこうしておきましょう。
さらに戦略形と展開形について、初めて学ぶときは
くらいに考えると良いです。これも乱暴すぎますけど。
ゲーム理論では「同時か、逐次か」と言った「時間」が重要なのではなく、相手の行動が観察できるかどうかが重要です。例えば、2人でじゃんけんをするとき、
としましょう。この場合は、時間としては交互に行動していますが、同時にじゃんけんをしているのと変わりありません(同時にじゃんけんすると、後出しっぽくなる人がいるのを考えると、こっちのほうがずっと「同時」かも知れない) 。先手は後手の行動を知らず、後手も先手の行動を知りません。この場合は戦略形ゲームになっていると言えます。
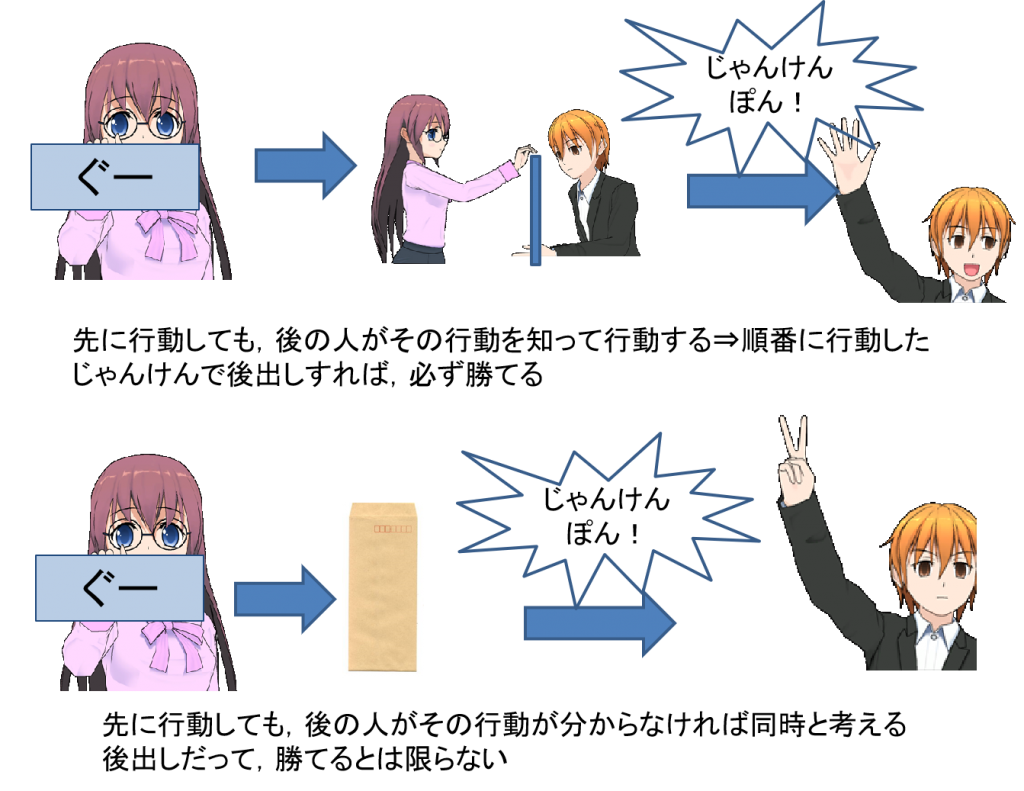
このように(すべてのプレイヤーが)他のプレイヤーの行動が観察できずに行動を選ぶ場合は戦略形ゲームです。オークションや競りを例に挙げれば、封印された紙に価格を書いて、最後に競り人がそれを開いて一番高額の人に出品された物を売る、と言った「封印入札」なども戦略形ゲームの典型的な例と言えます。
これに対して、チェスや将棋や囲碁では、自分より前に行動した人がどのような行動をしたかがすべて分かります。このようなゲームは完全情報ゲームと呼ばれますが、展開形ゲームで分析されるゲームの代表例です。オークションや競りでは、オークションハウスでの絵画の取引やマグロの競りなど、誰かが値段をつけたのを見て、それより高く買いたい人は更に高い価格をつける...などの「イングリッシュオークション」は展開形ゲームの典型例と言えます。同じ競りやオークションでも、ルールや形式によって違うゲームと考えられる点に注意です。
戦略形ゲームは「利得行列」と呼ばれる道具を用いて表現し、展開形ゲームは「ゲームの木」と言う道具を用いて表現します。戦略形ゲームと展開形ゲームについては、別の投稿で詳しく説明します。