クールノー競争の価格・生産量と社会的総余剰では、2社のクールノー競争におけるクールノー均衡を求める方法を説明しました。ここではそれを「最適反応曲線」(反応曲線、最適反応関数)と呼ばれる図で説明し、ナッシュ均衡との関連をより明確にします。
モデルの設定(再掲)
クールノー競争の価格・生産量と社会的総余剰で説明した設定を再掲します。そこから読んでいる方は、ここは飛ばして構いません。
- 同じ製品を販売している企業AとB。
- AとBの生産量をそれぞれ\(x_A、x_B\)とする。
- 市場全体の生産量を\(x=x_A+x_B\)とし、その価格\(p\)は$$p=a-bx$$で与えられるとする。
- 製品1単位の費用(限界費用)はAもBも\(c\)で同じとする。
- 企業Aの利益を\(\pi_A\)とおく。$$\pi_A=px_A-cx_A$$。
- 企業Aの利益\(\pi_A\)を最大にする\(x_A\)を考える。\(p=a-bx\)を代入し、\(x=x_A+x_B\)に注意すると\[ \begin{align} \pi_A &=\{a-b(x_A+x_B)\}x_A-cx_A\\&=-bx_A^2-bx_Ax_B+(a-c)x_A \tag{1} \end{align}\]とる。
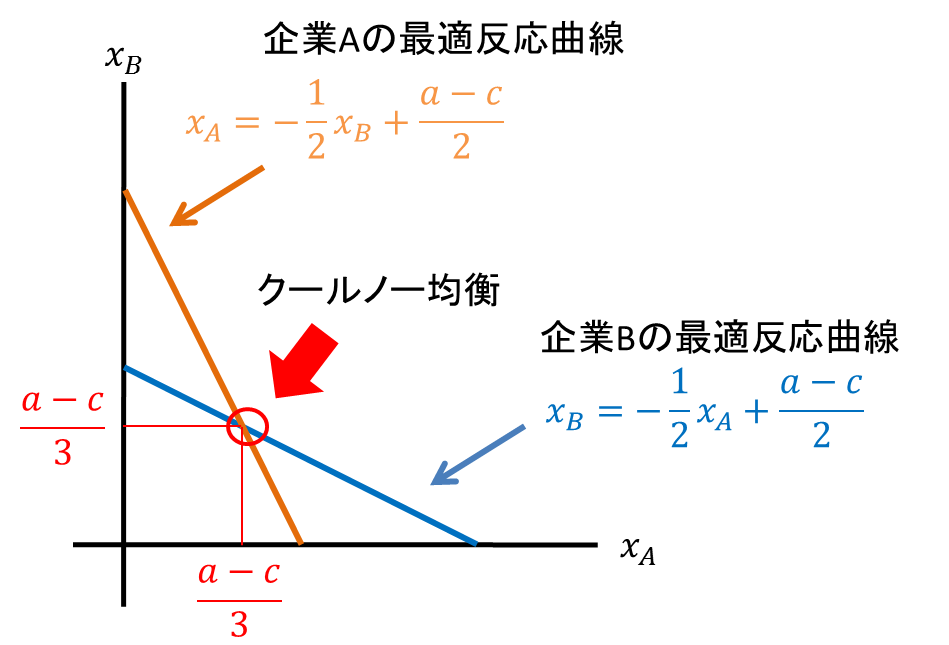
- 式(1)を最大にする\(x_A\)を求めるため、\(x_A\)で微分して0になるところを求める。(1)を\(x_A\)で微分すると、\(-2bx_A-bx_B+(a-c)\)。したがって\[-2bx_A-bx_B+(a-c)=0\]を解けば良く、これより\[x_A=-\frac{1}{2}x_B+\frac{a-c}{2b} \tag{2}\]となる。
- 企業Bの利益を\(\pi_B\)とおく。$$\pi_B=px_B-cx_B$$。
- 企業Bの利益\(\pi_B\)を最大にする\(x_B\)を求めると、\[x_B=-\frac{1}{2}x_A+\frac{a-c}{2b} \tag{3}\]となる。
- 式(2)と式(3)を、それぞれ「企業Aの最適反応関数」「企業Bの最適反応関数」と呼びます。
- 式(2)は企業Bの生産量\(x_B)\が与えられたときに、企業Aの利益を最大にする企業Aの生産量を表しています。
- 式(3)は企業Aの生産量\(x_A)\が与えられたときに、企業Bの利益を最大にする企業Bの生産量を表しています。
最適反応関数を図で書く-最適反応曲線
上記の最適反応関数を横軸に(x_A)、縦軸に(x_B)にした図(グラフ)に描いてみます。まず式(3)の企業Bの最適反応関数から考えてみます(⇒なぜなら、左辺は縦軸、右辺は横軸のグラフに慣れている人が多いからです)。式(3)のグラフを書いてみると、以下のようになります。

この式は切片が\(\frac{a-c}{2}\}で、傾きが-1/2の右下がりの直線になります。これは企業Aの生産量が与えられると、そのとき企業Bの利益が最大になる生産量がいくつであるかを示す曲線になるわけです。企業Bは、もし企業Aの生産量が決まれば、自分がもっとも利益が高くなる生産量が分かるわけですが、企業Aの生産量は決まっていません。そこでこれに式(2)の企業Aの最適反応曲線を描き、重ねてみます。

企業Aは、企業Bと縦軸と横軸が逆になりますね。切片と傾きは同じです。企業Aは、もし企業Bの生産量が決まれば、自分の利益を最大にする生産量が分かるわけですが、企業Bの生産量は決まっていません。
企業Bの生産量が決まらないと企業Aの生産量が決まらず、企業Aの生産量が決まらないと企業Bの生産量が決まらない。そこで「お互いが最適反応となる生産量の組」を選び合うことが答となると考えます。これがナッシュ均衡、またはクールノー均衡(またはクールノー=ナッシュ均衡)と呼ばれるものです。
ナッシュ均衡は20世紀半ばにゲーム理論で考えられたものですが、寡占市場の分析に限ると、それより100年以上も前にクールノーが上記の解を考えていたことによるため、このように呼ばれます。
お互いが最適反応となる生産量の組は、両方の直線が交わった点です(次の図)。この点は、式(2)と式(3)の連立方程式を解くことによって求められます。これを求めると、\[x_A=x_B=\frac{a-c}{3}\]となります。

以下も参考にして下さい。
