タグ: ゲーム理論
バックワードインダクションで展開形ゲームを解く
完全情報展開形ゲームとその解き方であるバックワードインダクション(backward induction)につい…
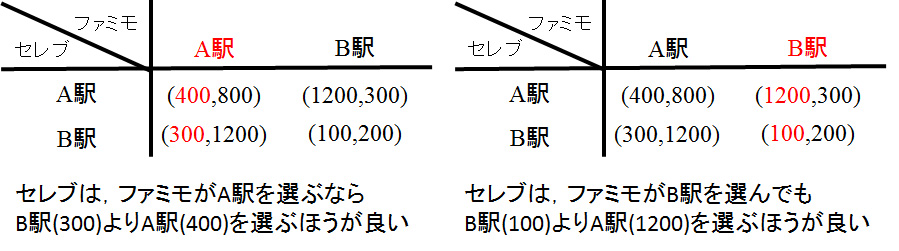
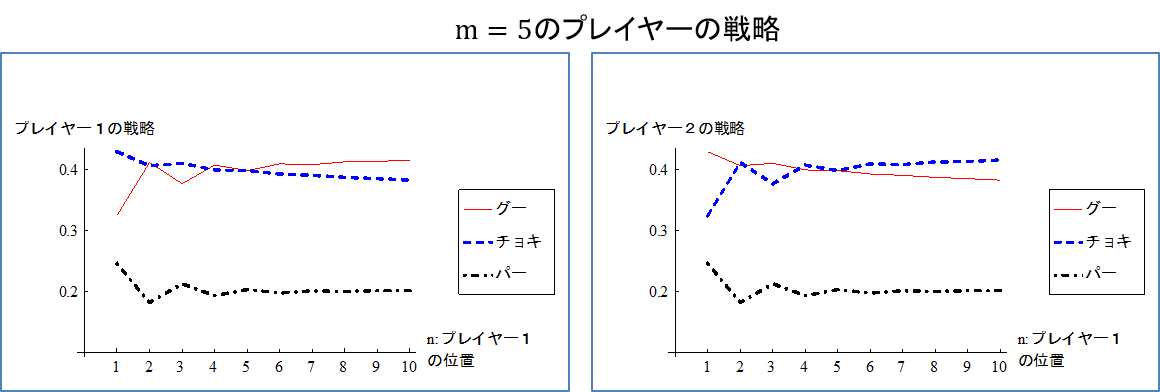
グリコじゃんけんのゲーム理論による解:ゴールに近いとチョキを出せ
グリコ・チョコレート・パイナップルという遊び(グリコ(遊び)、グリコじゃんけん、じゃんけんグリコ)は、ゴールす…
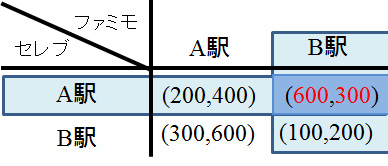
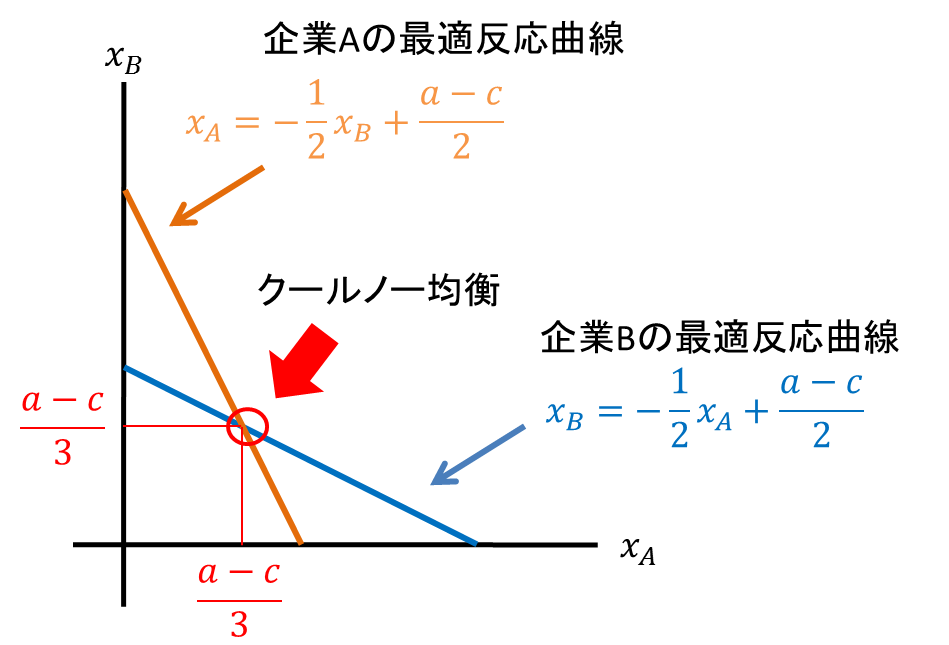
完全情報展開形ゲームとその解き方であるバックワードインダクション(backward induction)につい…


グリコ・チョコレート・パイナップルという遊び(グリコ(遊び)、グリコじゃんけん、じゃんけんグリコ)は、ゴールす…

