勝者の呪い、独立私的価値、相互依存価値

—

by

nabenavi
in ,

オークション理論の解説。ここでは勝者の呪いについて、図解で説明します。1つの財を売る単一財オークション理論では、商品に対して入札者がどのような価値を持っているかによってモデル化が異なり、それについても紹介します。

独立価値モデルと共通価値モデル

独立私的価値(Independent Private Value、 IPV)モデルは、個人によって商品の評価額(=価値）が異なるモデル、他者と自分の評価額が独立しているモデルです。スターやアイドルの所持品や遺品、絵画や骨董品のように「他人にとっては値打ちがなくても、自分にとっては値打ちがある」と言った商品に対して適用されます。この場合、入札者の評価額は入札者自身が分かっており、他者の評価額や情報に影響を受けません。

これに対し、すべての人にとって商品の本来の評価額が同じと考えるモデルを共通価値(Common Value、 CV)モデルと呼びます。 ただし入札者はその評価額を正確に見積もることができず、人によって「誤差」が生じます。これは石油や鉱山の採掘権、転売を目的とした商品の入札などに当てはまるモデルです。石油の採掘権（＝油田）の評価額は、そこから採掘される油田の埋蔵量、原油価格によって一意に決まります（採掘にかかるコストを考慮するときもある）。しかし、埋蔵量がどのくらいあるのか、原油価格がどのくらいになるかの予想が人によってずれる（誤差を持つ）ため、入札者がその油田に対して持つ評価額がずれてくるわけです。また転売目的に商品を落札するときは、転売時の商品価格が評価額となるはずです。最終的にこれは一意に決まりますが、入札時の予想は人によって異なるため評価額がずれてくるわけです。

一般的には、個人の評価額は不確実で他者の評価額い依存・相関すると考える相互価値依存モデル(Interdependent Value)と呼ばれるモデルもあり、共通価値モデルは、この特殊な場合として考えることができます。

勝者の呪い

共通価値モデルにおいては、一番高く商品を評価した入札者が、落札して商品を手に入れます。しかし、一般的にその商品の「共通価値=正しい価値」は、すべての入札者の評価額の平均値に近いと考えられ、一番高く商品を評価した入札者は商品を過大に評価しています。落札価格が実際の商品の価値を上回っている可能性もあり、このとき落札者は実際の商品の価値を知ったときに、それよりも高い価格で商品を買ってしまったと後悔することが予想されます。これを勝者の呪い（winner’s curse)と言います。

図解で知る勝者の呪い

J. McMillanのGames, Strategies, and Managers（邦訳「経営戦略のゲ‐ム理論」）の中に、瓶の中の硬貨のオークションの話があり、これがわかりやすい例だと思います。以下は、それを図解しましょう。

100円玉がぎっしり詰まった瓶をオークションするとしましょう。この瓶の価値は、美術品などと違ってお金そのものですから、100円玉の枚数によって、客観的に価値が決まるはずです。しかし何枚入っているかの推測は人によって異なるので、一人ひとり見積額が異なります。ここでは4人のオークションの参加者がいると考えましょう。

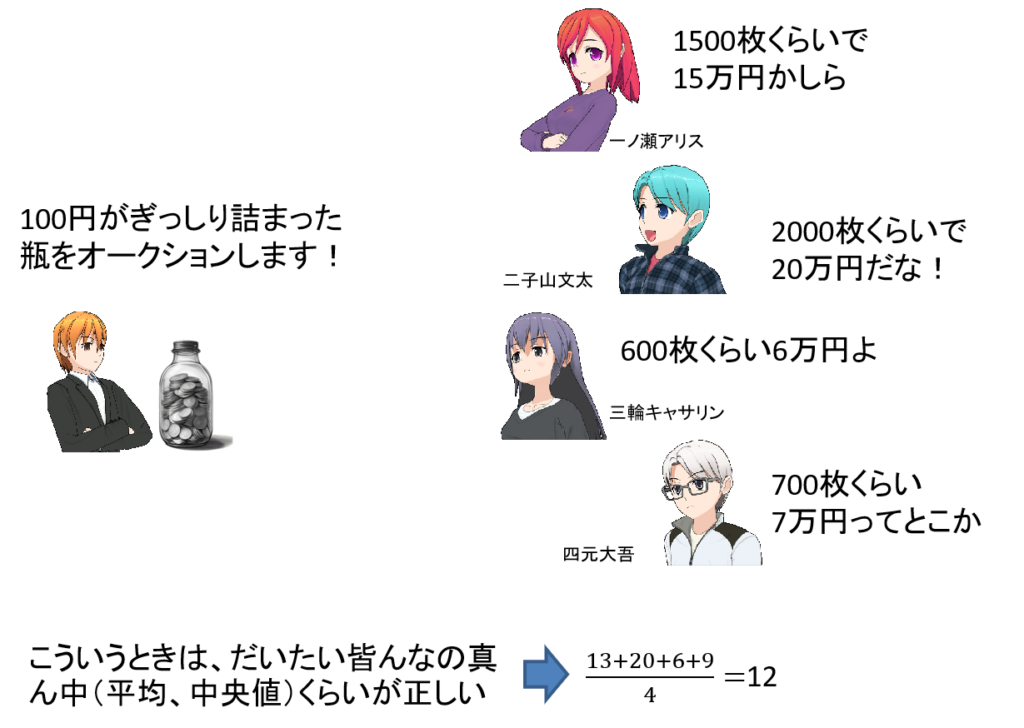
この例では4人の参加者の見積額は、15万円、20万円、6万円、7万円です。真剣に見積もっていれば、1番高い人や一番低い人は、推測が外れていることが多く、平均値や中央値が近い値になります。ですので12万円くらいが正解になります。

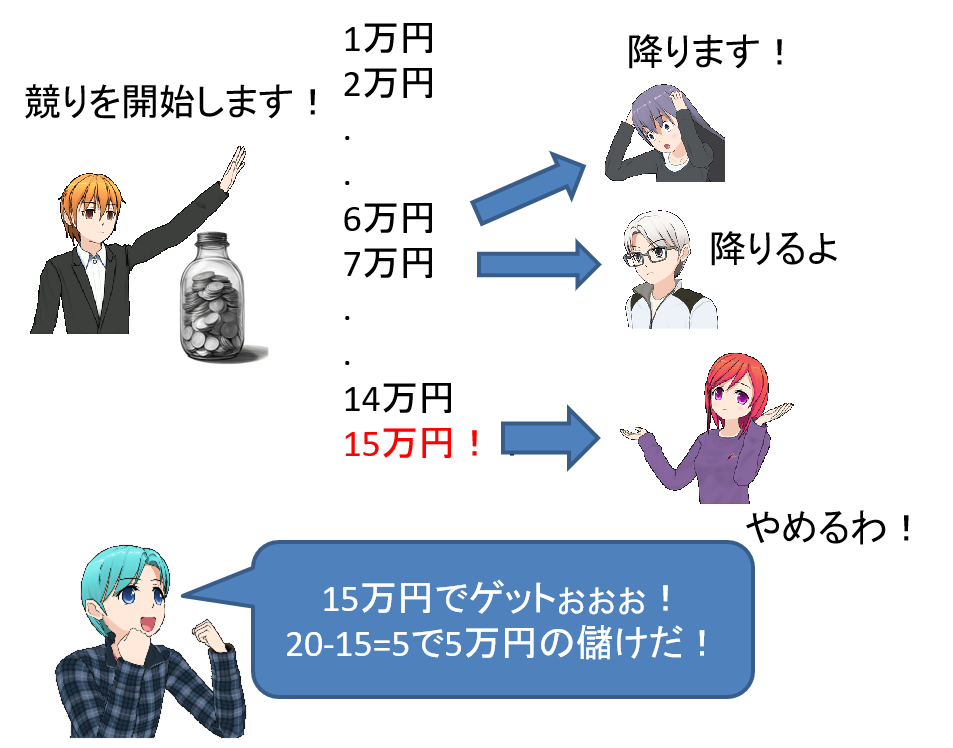
ここでは競りでオークションが行われたとしましょう。競りは2番目に評価額が高い人（1番評価額が高い人のライバル）が降りた時点で価格が決まるのは、世界んドプライスオークションと収益等価定理で述べたとおりです。ここでは文太（20万円と見積もった人）が落札します。

文太は、自分の推測額より安く買うことができたと喜びますが、彼が最高値で買ったということは、きっと彼は商品を高く見積もり過ぎていたのでしょう。結果を知って、彼は損をしたことを呪う（悪態をつく、文句を言う）でしょう。これがwinner’s curseです。

雄牛の重さ当て

私が共通価値モデルの話で思い浮かべるのは、「群衆の智慧（ジェームズ・スロウィッキー）」の冒頭に出てくる「雄牛の重さ当てコンテスト」の話です。

1906年にイギリスの科学者フランシス・ゴールドンは、イングランド西部の見本市における「雄牛の重さ当てコンテスト」で、ある調査をしました。このコンテストは、800人の参加者が「雄牛の重さ」を推測し、一番正解に近い人が商品をもらえる、というものでした。コンテストの参加者800人の予測のうち、判読不能な13人を除き787人の平均値を調べた結果、その平均値は1197ポンドでしたが、雄牛の実際の重さは1198ポンドで、ほとんど一致していたというものです。

この話は集合知＝群衆の知恵の代表例として知られています。これはこれで面白くて話したいこともたくさんあるのですが、それはまた別の機会に。

さて、このコンテストが雄牛のオークションであったら、どうでしょうか？ 牛肉1ポンドの価格はだいたい決まっているはずなので、 正しい雄牛の価格は牛肉1198ポンド分の「共通価値」になるはずです。そして、それは全員の予想の平均値とほぼ同じになります。しかしオークションを落札する人は、この雄牛の重さをもっとも重く予想した人になり、たぶんその人は落札後に勝者の呪いを持つことになるでしょう。

その商品の価値は一意に決まっていても不確実性があり、その価値を参加者が誤差を持って観察する場合は（ガウスを信じるなら）、参加者の評価額は以下の正規分布のように分布するはずです。

参加者の評価額の分布

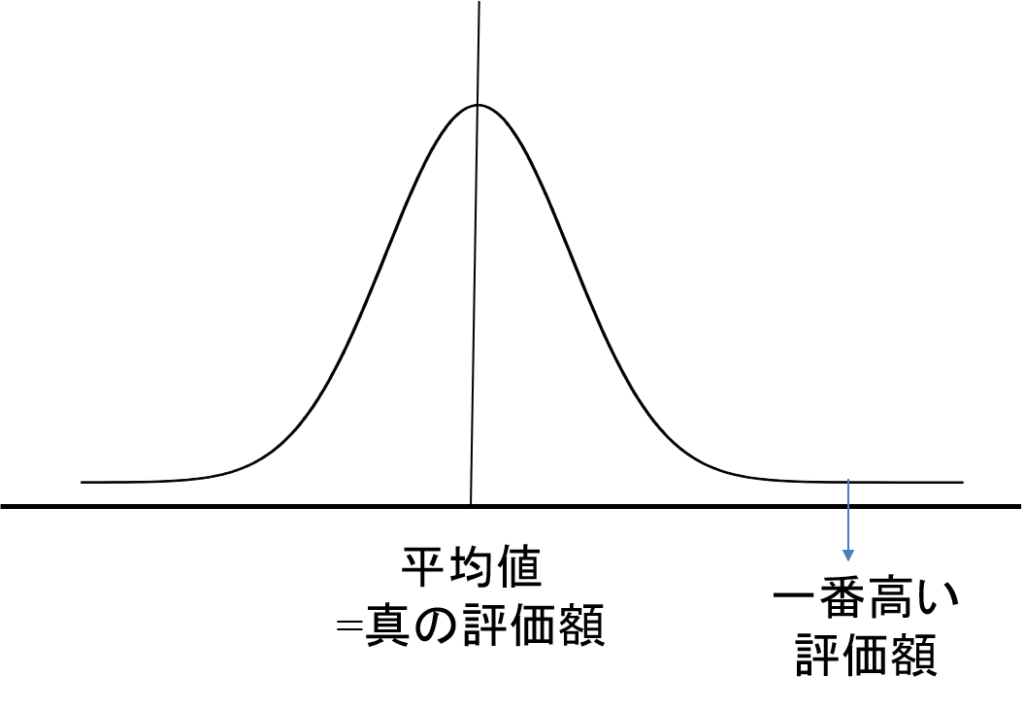
もっとも高い評価額は平均値＝真の評価額よりも、必ず高いところにあります。もしセカンドプライスオークションの説明で述べたように、参加者が自分の評価額を正直に入札したら、落札者は必ず勝者の呪いを起こすことになります。

共通価値モデルのセカンドプライスオークション

このことから共通価値モデルでは「セカンドプライスオークションでは、参加者が自分の評価額を正直に入札する」ということは成り立たないことが分かります。合理的な入札者は、自分が勝者になっても勝者の呪いが起きないように、自分の評価額よりも低く入札を行うという結果が得られます。

参考文献

関連投稿:

  1. オークション理論の本
  2. セカンドプライスオークションと収益等価定理をざっくり解説
  3. オークション理論