競馬のような多くの人が関わるような賭けには、少人数のゲームを解くゲーム理論より、金融市場を分析するファイナンスの理論が関係することは、既に述べたとおりです（たとえばこちら）。そこでは、ゲーム理論の意味での必勝法とは異なる意味ですが、必勝法や有利になる戦略、についての研究は存在します。
ここでは競馬の賭け方・戦略に関係する３つのファイナンス理論の考え方、市場の効率性、裁定、最適資産成長について紹介してみたいと思います。
裁定理論
裁定理論は、同じ価値を持つものには同じ価格がつかなければならないとする理論です。そのようなことが成り立たないときには、同じものを安い方から買い、高い方で売れば、必ず儲けることができるからです。このような取引は裁定取引と言われ金融だけではなく、一般的な経済取引の用語として使われます。ネットでの転売は、裁定取引の一種です。
裁定取引は、通常は「売る」と「買う」の両方の行為により利益を売ることができます。しかし競馬の場合は、異なる種類の馬券にオッズの歪みがあることを利用して利益を得る行為を指します。このようなことは、ほとんど起きないのですが、理論上は考えることは可能です。以下にその例を説明しましょう。
ここで3頭しか走らない競馬のレースで単勝と馬連が発売されているとします。馬の番号を1,2,3とし、1と2の馬の単勝が4.1倍ついていたとします。さらに1-3と2-3の馬連もオッズが4.1倍だったとします。この場合1と2の馬の単勝と、1-3と2-3の馬連の4種類の馬券をすべて同じ金額だけ買えば、1,2,3のどの馬が勝っても必ず儲かることができます。
試しに1万円ずつ買ったとすれば（購入金額は合計4万円）、1か2の馬が勝てば払戻金は4万1千円、3の馬が勝ったときは馬連の1-3か2-3のどちらかが必ず当たるので払戻金はやはり4万1千円で、どの馬が勝っても必ず千円儲けることができます。
どのような場合に、これが起きるの考えてみます。主催者の控除率が25%であるとすると、1と2の馬の単勝が18%買われ、3の馬の単勝が63%であると、1と2の馬の単勝オッズは4.1倍になります（3の馬の単勝オッズは1.1倍）。反対に1-3と2-3の馬連が18%買われ、1-2の馬の馬連が63%買われると1-3と2-3の馬連は4.1倍になります（1-2のオッズは1.1倍）（下図）。
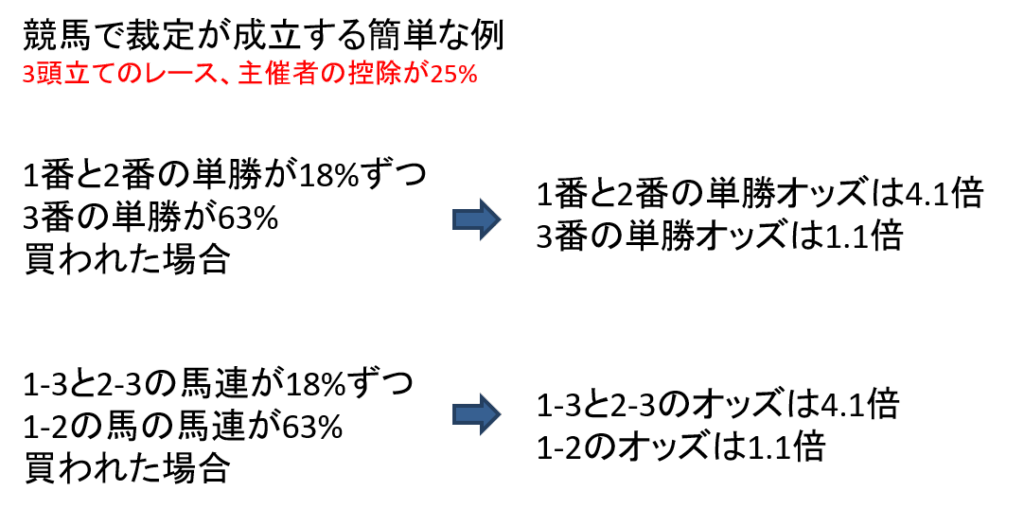
3の馬はほとんど勝つ可能性は少ないが、アイドル的な馬で単勝だけが買われる場合に、このようなことは起きうるかもしれません。
実際に裁定が起きることはほとんどありません。また大量に馬券を買うことで、自分がオッズを下げてしまうこともあるため、これを考慮して裁定が起きてたことを示すことは用意ではありませんが、神戸大の芦谷教授は2010年9月の荒尾競馬で、裁定取引が実行可能であった例を示しています。
芦屋政浩(2012), 日本の公営競馬における「競馬必勝法の具体例」, 国民経済雑誌, 205巻6号（2012-06）, 81-91.
市場の効率性
競馬に関連するファイナンスの理論の１つとして、市場の効率性が挙げられます。市場の効率性を知るには2013年のノーベル経済学賞について知ることが良いでしょう。このときの受賞者の1人、ユージン・ファーマは効率的市場仮説(Efficient Market Hypothesis: EMH)と呼ばれる理論によって、株式市場の価格の決まり方を説明しようとしました。
効率的市場仮説は、株式市場で必要な情報はすべて価格に織り込まれているという考え方で、良い業績の企業の株価は高くなり、悪い業績の企業の株価は低くなるとする理論です。この効率的市場仮説の検証と称して、古くから競馬は研究材料として用いられてきました。効率的市場仮説が正しければ、勝つ確率の高い馬のオッズは低くなり、低い馬のオッズは高くなるはずなのです。
もっと正確に成り立つなとすれば、例えば単勝においては、賭けられたお金のうち、50%のお金が賭けられた馬の勝つ確率は50%、1%の金額が賭けられた馬の勝つ確率は1%と、賭けられたお金の比率が馬の勝つ確率を反映すると考えられます。言い換えれば「３倍のオッズの馬が勝つ確率は、６倍のオッズの馬が勝つ確率の２倍」のように、オッズの比率（の逆数）は馬の勝つ確率の比率を正しく反映しているはずです。
これに対して、2013年ノーベル経済学賞のもう１人の受賞者であるロバート・シラーは行動経済学の研究者で、競馬のデータで効率的市場仮説が成り立たないことを示しました。シラーは、アメリカやイギリスの競馬のオッズを調べ、本命馬は市場効率性によるオッズの計算値よりも勝つ確率が大きく、穴馬は確率が小さくなることを示しました。つまり人々は、穴馬に過大に賭け、本命馬に過小に賭ける傾向があるということです。つまり、競馬において人々は非合理な判断をすると考えられます。この傾向は本命－穴馬の偏り(Faviorate Longshot Bias:FLB)と呼ばれており、シラーの研究だけではなく、いくつかの研究により実証されています。
なお日本では本命－穴馬の偏りは成り立たないとする研究もあります。これについては、またの機会に詳しく述べることとします（私が監修した競馬の経済学のコラムに、少しだけこのことについて書きました）。
最適資産成長
手持ちのお金の何％を投資に回し、何％を残す（安全な資産に預けるか）という問題は、最適資産成長の問題と呼ばれます。儲かれば、その儲かったお金をさらに投資に回し、損失が出た場合は、手元に残したお金を投資に回す。これを繰り返したときに、最終的に一番資産が大きくなるにはどうすれば良いかを考える問題です。
賭けによる期待値がプラスのときは、ケリー規準やケリーの公式という方法が知られています。しかし、競馬のような期待値が負になるギャンブルにはこの公式は使えません（期待値が正でも、実際には投資対象の確率分布を正確に知ることが難しいため使うことが難しい）。
このような最適資産成長の問題の場合、何をどのような条件で最大化するのかによって答は異なってきます。期待値が正の場合であってもです。ですので、問題を正確に定義しなければ答は出ません。
期待値が負になる場合、ルーレットの赤か黒のどちらかに賭けるような2択の問題で、ある目標となる金額に達する確率が一番高くなるためには、手持ちの資産をすべて一度に賭ける「bold strategy」という方法が最適であることが、古くから知られています。
Dubbins, Lester E and Savage, Leonard J. (1976), How to Gamble If You Must. Inequalities for Stochastic Processes, Dover Publications.
私が監修した「競馬の経済学」という本です。競馬のお金にまつわる様々な話題を詰めました。ここ書いたような話題は少ないですが、よろしければ、ご購入ください！
※このページに関する質問は受け付けていません。