ナッシュ均衡を列挙計算するwebアプリは、戦略が10個以下の2人戦略形ゲームのナッシュ均衡をすべて列挙します。
2人戦略形ゲーム(以下、bimatrix game)のナッシュ均衡の興味深い例を、アプリで計算してみました。
\(2 \times 3\)ゲームのナッシュ均衡(Von Stengel (2002))
- von Stengel (2002), Computing Equilibira for Two Person Games, in (eds.) R. J. Aumann and S. Hart, Handbook of Game Theory, vol.3 Chapter 45, Elsevier. doi.org/10.1016/S1574-0005(02)03008-4
von Stengel (2002)の例で使われた利得行列
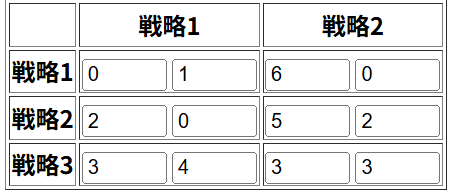
bimatrix gameのナッシュ均衡を1つ見つける古典的で代表的なアルゴリズムであるLemke-Howson algorithmの例として使われています。Lemke-Howsonアルゴリズムが多面体上でどのように動くかが、よく分かる解説論文です。現在では使われていないのかもしれませんが、線形計画法の単体法などとともに、とても美しいアルゴリズム+理論だと思います。
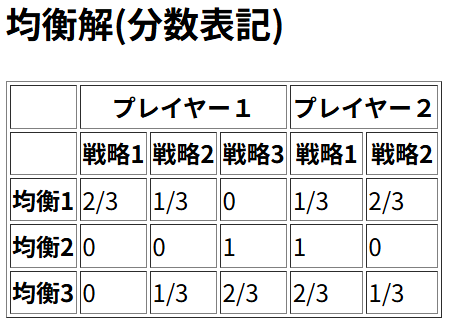
Lemke-Howson Algorithmでは、結果として均衡3が計算されます。
O’Neill実験
O’Neill (1987)は、4枚のカード(1,2,3,J)を使った2人ゲームで被験者への実験を行っています。このゲームではプレイヤー1と2が同時にカードを1枚出し、以下の表で○であればプレイヤー1が勝ち、☓であればプレイヤー2が勝ちます。勝ったプレイヤーは負けたプレイヤーに5セント払います(最初に2.5ドルが与えられています)。
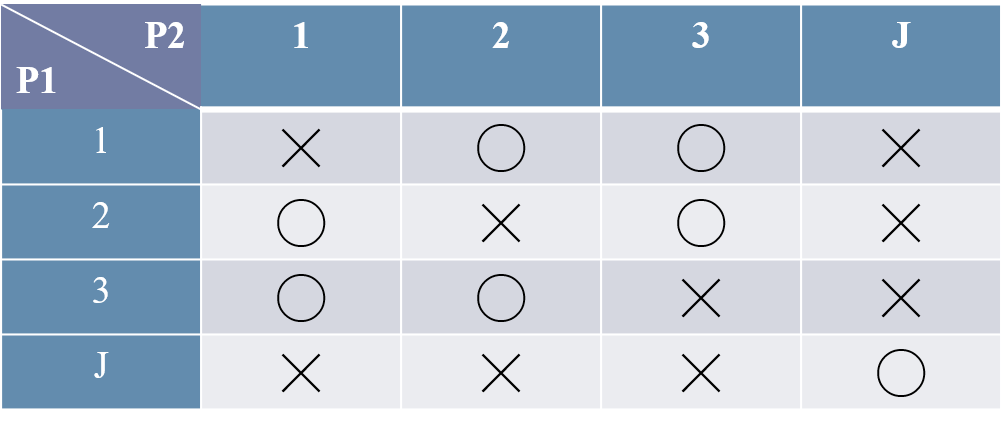
実験結果を集計すると、被験者が選んだ戦略の頻度は混合戦略のナッシュ均衡に一致することが示されました。このゲームの混合戦略ナッシュ均衡は、簡単には計算できるものではありません。そのようなナッシュ均衡が、実験によって実現するという事実は興味深いものです。
これに対して、Brown and Rothenthal(1990)はO’Neill のデータを再検討し、集計した値はナッシュ均衡になっていることは否定できないが、個々のプレイヤーが混合戦略のナッシュ均衡を確率的には選んでいるとは言えない、ということを示しました。
- O’NEILL, B. (1987), Nonmetric Test of the Minimax Theory of Two-person Zerosum Games,” Proceedings of the National Academy of Sciences, U.S.A., 84, 2106-2109.
- J. Brown and R. Rosenthal (1990), Testing the Minimax Hypothesis, A Reexamina- tion of O’Neill’s Game Experiment,” Econometrica, 58, 1065-1081.
利得行列は以下の通りです。
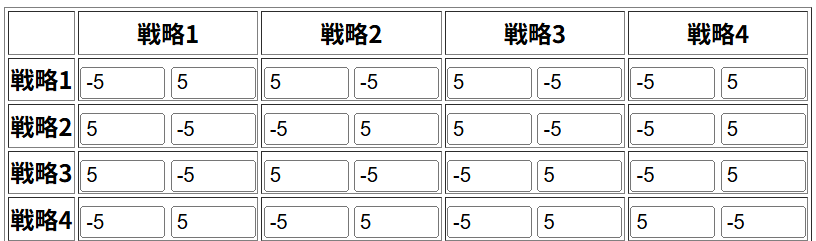
5セントに合わせて利得は5と-5にしましたが、利得を各プレイヤーごとに利得を正の一次変換をしてもゲームは同等で均衡は変わらないので(期待効用理論)、以下の利得行列のように「勝ったほうが1、負けたほうが0」としても同じ結果になります(覚えておきたいTipsですね。)。
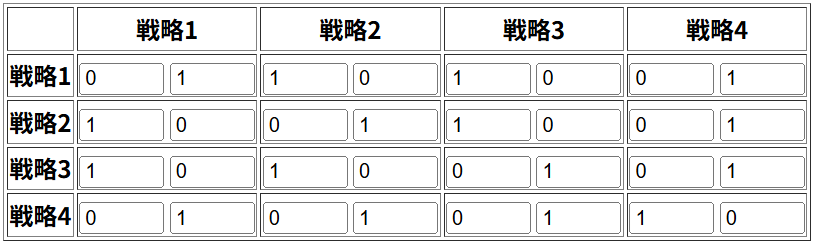
このゲームはゼロサムゲームなので線形計画法でも解くことができます。アプリで解くと以下のような結果になります。

ナッシュ均衡は1つです。この結果を人間(被験者)が計算するのは難しいですよね!個々の人は混合戦略を使っているとは言えず、何らかの「癖」に従っているようですが、被験者全体で使われた戦略頻度の集計値が混合戦略に従っていることは驚くべき事実です。
\(6\times 6\)のナッシュ均衡の最大数(Von Stengel (2002))
- von Stengel (1999), B. New Maximal Numbers of Equilibria in Bimatrix Games. Discrete and Computational Geometry 21, 557–568. doi.org/10.1007/PL00009438.
\(n☓n\)の利得行列(退化していない)の混合戦略を含めたナッシュ均衡が最大でいくつあるかという問題です。\(n=2\)のときは3個、\(n=3\)のときは7個です。
7個あるのは、以下のような例ですね。
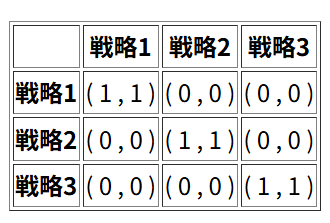
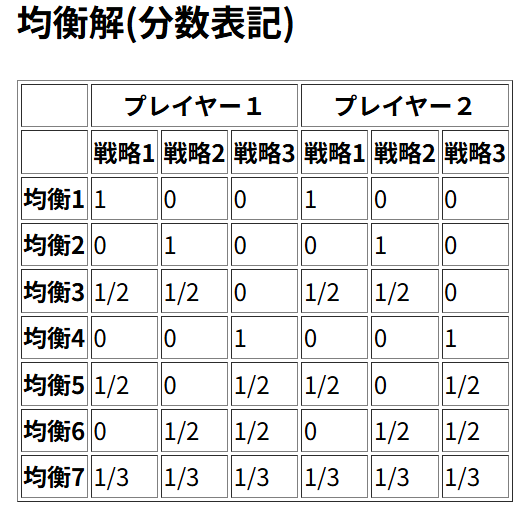
\(n=4\)のときはどうでしょう?予想がつきますね。以下の例では、ナッシュ均衡は15個になります。
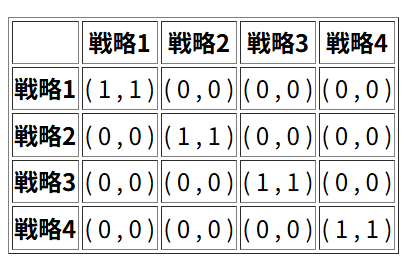
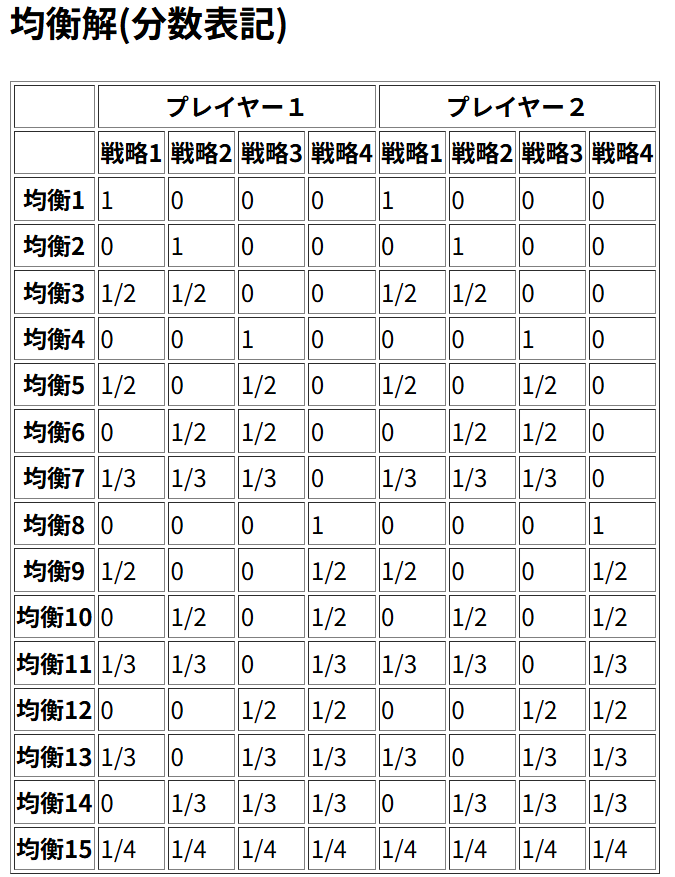
これ以上、ナッシュ均衡の個数があるゲームはなさそうです。確かに\(n=4\)のときは15個が最大で、 H. Keiding (1997)、A. McLennan and In-Uck Park (1999)によって証明されています。この証明は結構難しいんです(私は理解できていません。)
- A. McLennan and In-Uck Park (1999) Generic 4×4 Two Person Games Have at Most 15 Nash Equilibria, Games and Economic Behavior, 26, 111-130.
- H. Keiding (1997) On the Maximal Number of Nash Equilibria in a Bimatrix Game, Games and Economic Behavior, 21, 148–160.
これをもとにQuint and Shubik (1997)は「\(n☓n\)のナッシュ均衡の最大個数は\(2^n-1\)である」と予想しました。なるほど、そんな気もします。
この予想が正しければ\(n=6\)のときは(\(2^n-1=63\))で63個です。上の例のように対角線に1を並べて、他を0にすればナッシュ均衡は63個になります。自分は、どう考えても、それがナッシュ均衡の最大個数のように思えました。
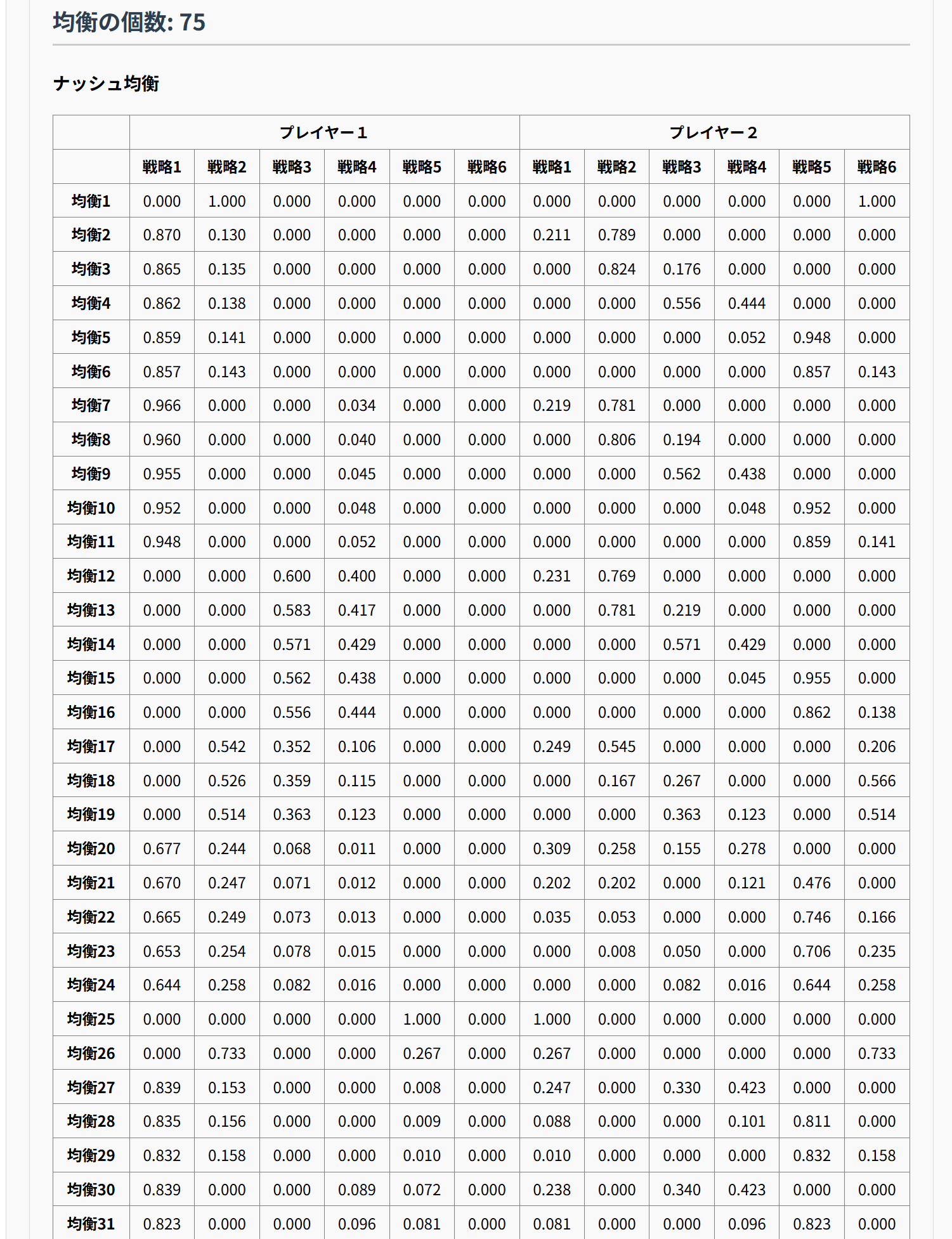
しかしですよ。von Stengelは、\(n=6\)のときナッシュ均衡が75個あるようなゲームを作り、この予想が誤りであることを示しました。(von Stengel(1999))。自分は最初にこれを見たときぶったまげましたよ!
以下が、そのゲームです。
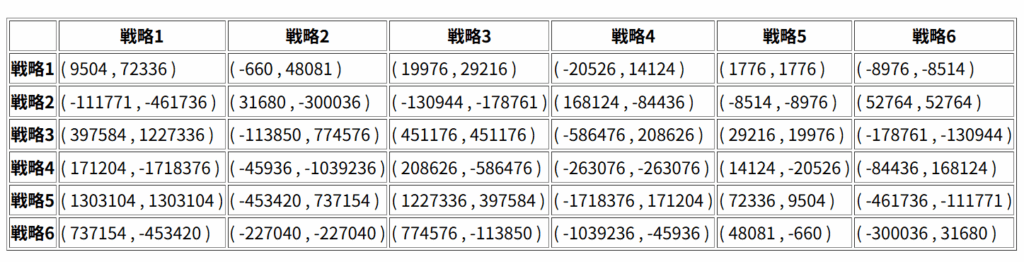
アプリで計算してみましょう。
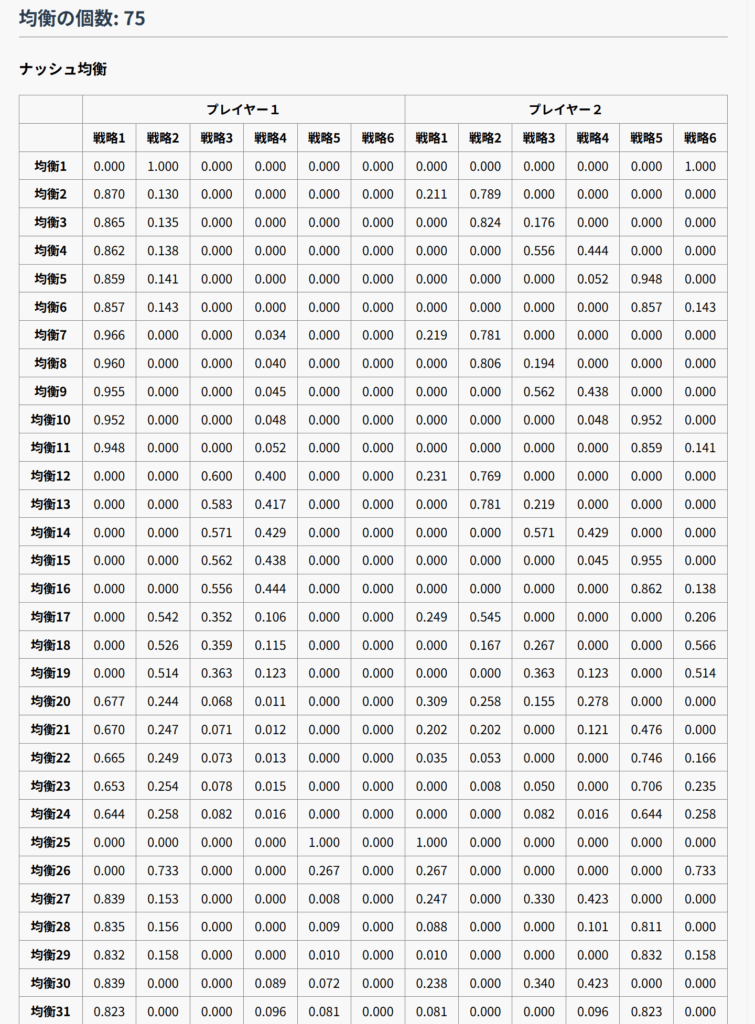
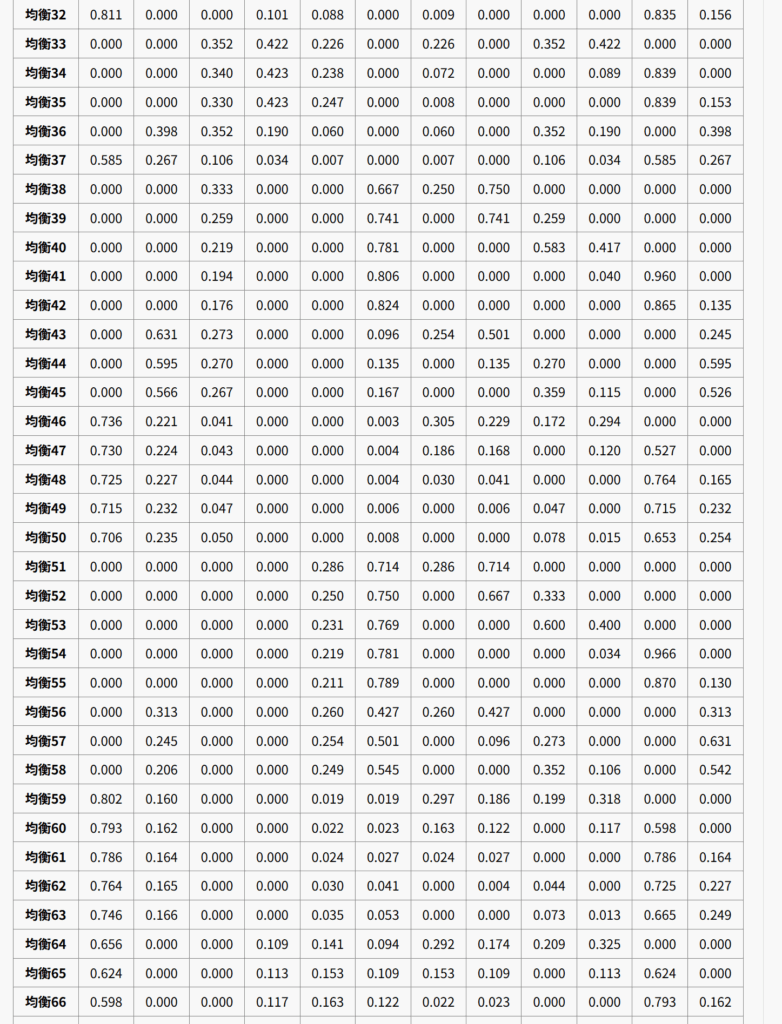
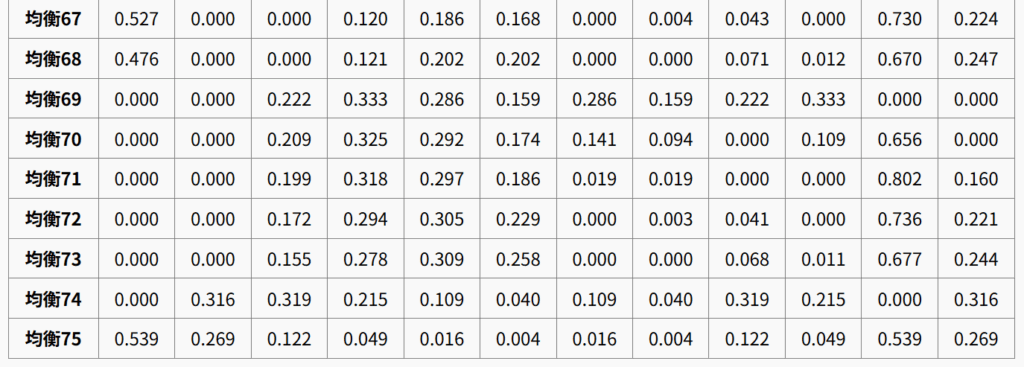
von Stengel(1999)は、この例を踏まえて「最大数の上限」について論じています。
ちなみに私のアプリは、2025年5月までは計算誤差をうまく処理できずに、上記の例が正しく計算できていませんでした。計算途中で、連立方程式の解がすべて正であるかどうかを判断する必要があるのですが、ここの処理を気をつけないといけなかったのでした。
現在は、正しく計算できています。また、このために手入力だけではなく、csvファイルで入力できる機能も追加しました。
そもそも、ナッシュ均衡の列挙計算アプリを作ったのは、この例を確かめるためでした。
馬場先生のゲーム
青山学院の馬場先生から「以下のようなゲームを作ったのだが、ナッシュ均衡がうまく計算できない、助けてください」とメールが来ました。「エクセル操作を勉強中の高3の息子に、5元連立方程式をエクセルで解かせようと思い作った」ということです。
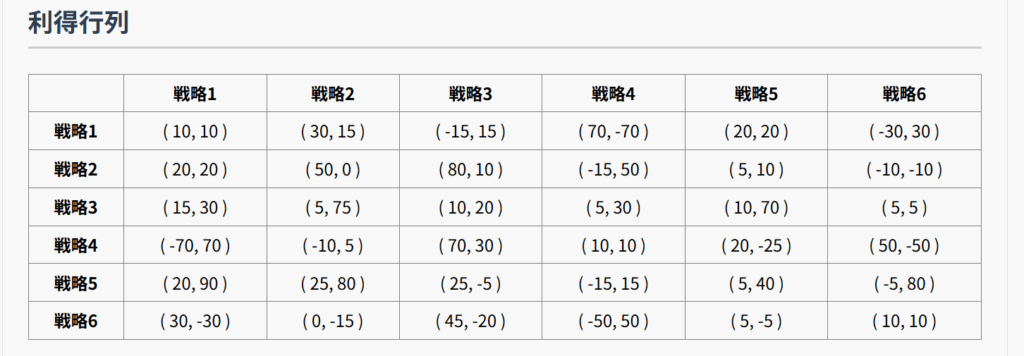
アプリで解いてみます。
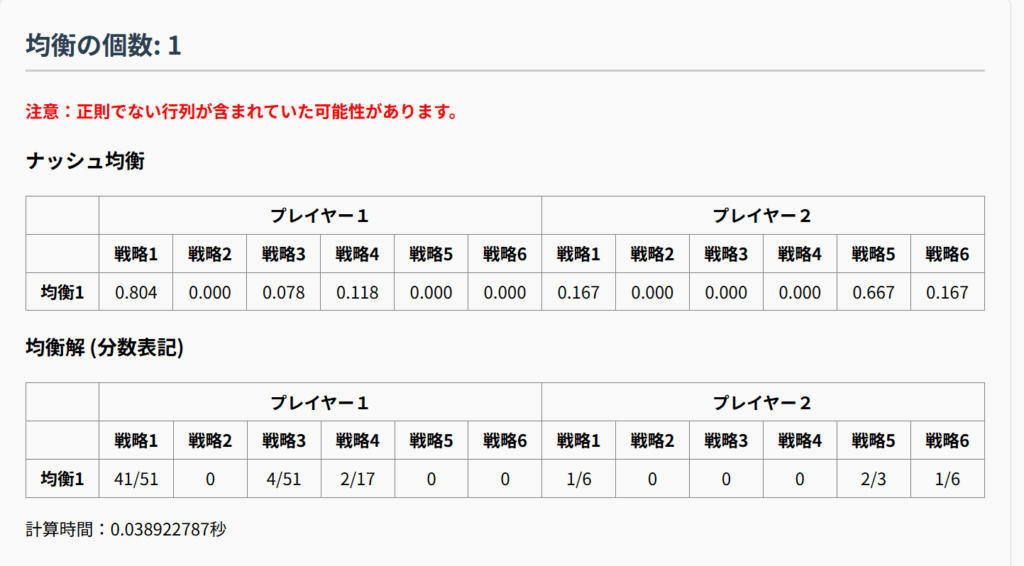
このゲームは「戦略が6つで、純粋戦略のナッシュ均衡がないにも関わらず、ナッシュ均衡が1つ」という興味深いゲームに思えます。ただ「正則でない可能性がる」というメッセージがあることから、行列が退化していて、他にも均衡があるのかもしれません。
均衡では確率が0になっている戦略がありますが、この戦略が何らかの混合戦略に支配されているかどうかは、今のところ確かめていません。
これを手作業で作られる(息子のために)のですから、馬場先生はすごいなと改めて思った次第です。