※本記事に対してメールを頂き、それを受けて少し書き直しました。ありがとうございました。(2024/03/16)
※修正した記事が間違ってましたので、直しました。ご指摘頂いた方、ありがとうございました(2024/03/22)
モンティホール問題とは？
まずモンティ・ホール問題について説明しておきます。
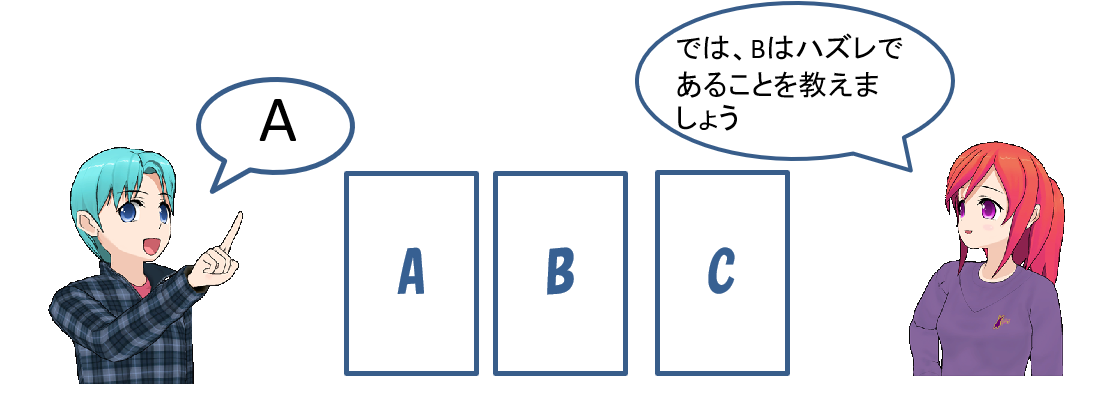
司会者（モンティ・ホールさん）と回答者がいて、回答者の前にはA、B、Cの３つのドアがあります。1つのドアは当たりで豪華な商品があり、回答者はそのドアを当てます。2つのドアはハズレです。回答者が「当たり」のドアを当てる、というものです。
まず、回答者がが当たりと思うドアを１つ選びます。ここではAを選んだとしましょう。司会者は、当たりのドアを知っていて、回答者が選ばなかったドアのうち、1つのドアがハズレであることを示します。ここではBのドアがハズレだと示されたとしましょう。
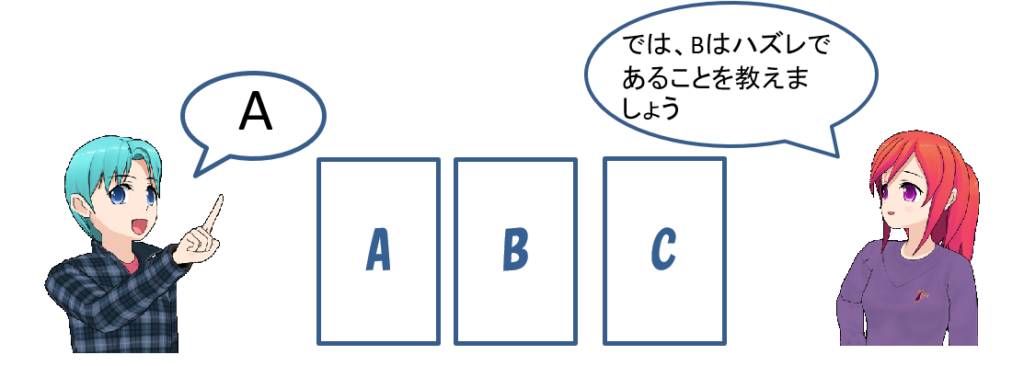
ここで司会者が回答者に言います。「あなたには、もう一度ドアを選び直すチャンスがあります。そのままにしますか？それとも変えますか？(stick or switch?)」
今回の場合、Aのまま留まるか？Cに変えるか？ということになります。
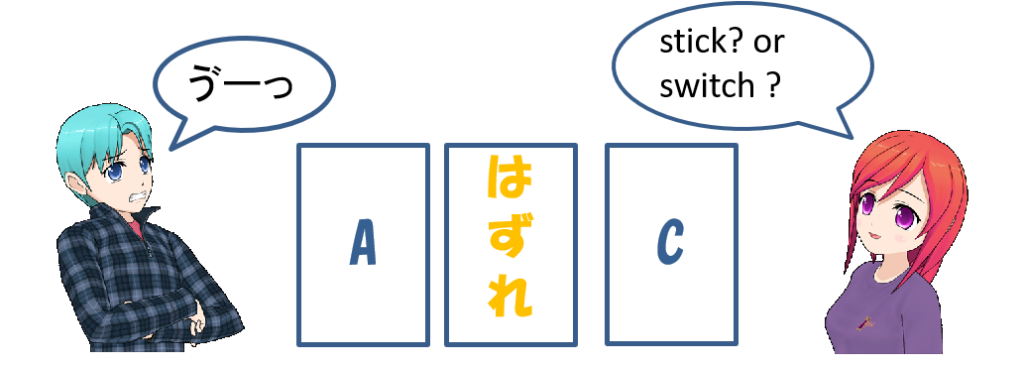
さて、回答者はドアを変更すべきでしょうか？それとも留まるべき？
この問題、AとCの2枚のドアのうち1つが当たりなので、変えても留まっても当たる確率は半々(1/2)のように思えます。しかしこの問題の答は「変えたほうが良い」です。留まる（Aのまま）だと当たる確率は1/3、変えると(Cに変更）当たる確率は2/3になります。
なぜ、そうなるかについては、ベイズの定理を使って、数々のネットの情報や本で説明されています。拙著「ゼミナールゲーム理論入門」でも「一歩ずつ学ぶ ゲーム理論」でも、もちろん解説されています。
「直観的説明」には注意が必要
「お、じゃあネットで検索してみようか！」と思ったあなた！ちょっと待ってください。この問題に対して「直感的に説明すると…」とした説明には、間違っていることが結構あります。本稿の意図は「直感的な説明は間違っていることが多いので、ベイズの定理で理解しましょう」ということなんです。
特に「確率は変わらない」的な説明は、間違いです。例えば「最初に選んだドアが当たる確率は1/3、それ以外が当たる確率は2/3だから、ハズレのドアを開けた後も、最初に選んだドアの当たる確率は1/3で、それ以外が当たる確率は2/3」と言う説明は誤りです。正しい説明は「情報によって確率は変わる」です。
最初に各ドアの当たる確率が等しいと、この「確率は変わらない」という説明も（たまたま）正しいように見えるのですが、最初に当たりやすいドアと、当たりにくいドアがあると考えれば、この説明が正しくないことが分かります。
A、B、Cのドアがあり、どれか１つが当たりだとします。ただし、Aのドアは当たりやすく当たる確率は0.5、Bは当たりにくく当たる確率は0.2、Cは0.3であるとします。
回答者は最初に（当たりやすそうな）Aのドアを選んだとしましょう。
ここで司会者（解答を知っている）は、選んでないドアからハズレのドアを1つ開けます。Bのドアが当たりならCが開き、Cのドアが当たりならBが開きますね。さて、Aのドアが当たりの場合はBとCのどちらを開けても良いのですが、ここで司会者がBとCのドアを開ける確率は同じ1/2であるとします（ここを変えると答も変わります）。
さて、司会者がBのドアを開けて、ハズレであることを示したとします。回答者はドアを変えたほうが良いんでしょうか？
「最初にAのドアが当たる確率は0.5、それ以外が当たる確率は0.5、この確率は変わらない」という説明だとフィフティ・フィフティで、変えても変えなくとも確率は1/2のような気がします。
しかし、この場合はAのドアのままだと当たる確率は5/11、Cに変えると当たる確率は6/11です。この場合は、やはりドアを変えたほうが良いです。
ちなみに司会者がCのドアを開けてハズレであることを示すと、 Aのドアのままだと当たる確率は5/9、Bに変えると当たる確率は4/9です。この場合は、ドアを変えない方が良いのです。つまり、この場合は「司会者がBのドアを開けたときはCに変えたほうが良く、Cのドアを開けたときはAのドアのままが良い」です。
モンティ・ホール問題の本質は、ドアを開けたことが情報になっていて、開ける前の事前確率と開けた後の事後確率が変化している、ということにあります。なので「元の確率と変わらないから」 的な説明は間違っていることが多いのです。
A、B、Cのドアが当たる確率が、それぞれ0.54、0.13、0.33として同じ状況だとしましょう。司会者がドアを開ける前は「Aのドアが当たる確率は0.54、それ以外は当たる確率は0.46」です。司会者がBのドアを開けたとき、回答者はドアを変えたほうが良いのでしょうか？確率は変わらない」のならば「Aのドアが当たる確率は0.54」なので、変えないほうが良いですね。
しかしこの場合も「Aのドアのままだと当たる確率は0.45、Cに変えると当たる確率は0.55」になります。司会者がドアを開ける前は、Aを選んだ方が、それ以外のドアが当たる確率より高いにも関わらずです！
計算方法は、ベイズの定理を勉強してください。このように、この問題は「直感的な」理解はなかなか難しいのです。ネットの説明でも「情報によって確率は変わる」という回答を読むと良いでしょう。
なぜ間違いを犯すのかという研究がある
認知科学や認知心理学では、なぜ人間はこの問題に対して正しい答が出せないのか、どのような点が間違いを引き起こすのかについて研究されています（いました）。興味にある方は、以下の本を参考にしてください。
市川 伸一 (著)、日本認知科学会 (編集)、確率の理解を探る―3囚人問題とその周辺 (認知科学モノグラフ 10) (1998)/5/1
ちなみに、若い頃、先輩の金融工学の大家KJ先生(川喜田二郎氏ではないよ）に「認知科学にこんな研究があります」と話したことがあります。そのときKJ先生曰く：
渡辺君。こんな研究は意味ないよ。
皆んながベイズの定理を正しく理解すれば良いだけだ！
…でした。直感的な理解ではなく、ベイズの定理で理解しましょう。