ナンバーズは物理的な機械でランダムに数が選ばれるため当選番号を予測することはできません。しかし、過去の当選番号の系列を調べてみると、何らかの傾向があるように思えて番号が予測できるような気がしてきます。
このような「確率・統計上のゆらぎ」と「人間の幻想」については多くの文献が考察をしていますが、ここでも、1つの例を取りあげて、このような幻想と「大数の法則」について、考えてみたいと思います。
こちら(賞金額の高いナンバーズの番号)も参照してください
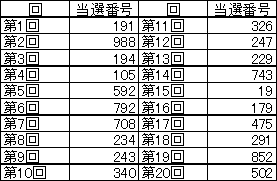
20回までのナンバーズ3の番号の60個の数字を考察
このような傾向の中で一番単純なものは、頻度の多い数と少ない数を調べるものです。ここでは、ナンバーズ3の20回目までの当選番号において、どの数字が何回出たかを調べながら、このことを考えてみます。皆さんもここで、ナンバーズが始まって、まだ20回の時の気持ちになり、考えてみてください。
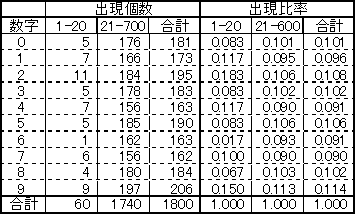
ナンバーズ3は1回の抽選で3つの数字が選ばれて、それを当てるくじです。20回までには、合計60個の数字が出現します。以下の表1には20回までの当選番号、表2には各数字の出現個数をまとめました。
※連載当時は紙の資料しかなかったんで自分で入力しました。現在はナンバーズ3(NUMBERS3) 過去の当せん番号案内に公表されています。
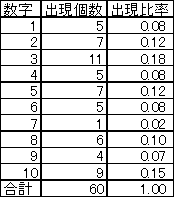
ここで20回目までの当選番号を見ると、6が1回しか出ていません。20回までには全部で60個の数字があり、平均で1つの数字は6回も出現するのはずなのに、たったの1回!これは何らかの傾向があると言わざるを得ない!という気になってきます。
まず、これはそんなに起こり得ない現象なのでしょうか?そこで10個の数から、でたらめに1つ数字が60回選ばれる時に「6」が1回以下しか出ない確率を求めてみましょう。まずはじめに「6」が1回も出ない確率を求めてみると、これは6以外の数字が60回すべて選ばれる確率であり、$$0.9^{60}=0.002$$ となります。次に「6」が1回だけ出る確率を計算するとです。合計すると「6」が1回以下しか出ない確率は$$_1 C_{60}\times 0.1 \times 0.9^{59}=0.014$$で、1.4%の確率でこのような現象が起こることが分かります。しかし、「6」に限らずに、少なくとも1つ以上の数字が1回以下しか出ない確率と考えると更に高くなるわけで(約14%)、このようなことは決して珍しい事ではないことが分かります。

20回目以降に6が出やすいわけでも、出にくいわけでもない
20回目まで、ほとんど6は出ていない。しかも、それ以降も6の出現確率は低い。そうならば「やっぱり6が出にくい」のかと言えば、そうではありません。20回目までの6の出現比率が1.7%であったのに対して、600回目までの合計の出現比率は9.1%になり10%にぐっと近づいていることが分かります。
数の出現比率が10%に近づく理由は、21回目から600回目まで「全体の個数(サンプル数)」が多くなり、20回目までの影響が無視できるほど小さくなったからで、6が多く出たからではないのです。
詳しく説明しましょう。1回から20回まででサンプルとなる数字の個数は60個(20回x3)です。60個の10%は6個。ここで「6」が出た回数は1回で、5回少ないことになります。
これに対して、1回から600回までサンプルとなる数字の個数は1800個です。1800個の10%は180個ですが、「6」が出た回数は163回で、17回も少ないことになります。
しかし出現比率で見ると、1回から20回までの「6」の出現比率は1/60=0.017で1.7%。これに対して1回から600回までの「6」の出現比率は163/1800=0.093で9.3%。つまり10%にぐっと近づきます。サンプル数が60から1800に増えているため「60の中で5回少ないのと、1800の中で17回少ないのでは、後者のほうが誤差範囲がずっと小さい」というわけです。
6に限らずすべての数字の出現比率を見てみると、20回目まででは1.7%から18.3%と幅があるのに対し、600回目になると9.1%から11.4%と、10%の周りに近づいていることが分かります。
大数の法則から、サンプル数が多くなれば10個の数の出現比率は確率上の平均値である10%にに近づいて行きます。しかし、平均値に近づくまでにはかなりのサンプル数が必要となることが分かります。
単純な数の出現比率だけでこうですから、「3が出た次の回には6が出やすい」「前々回に3が十の位に出現し、前回に9が出た場合は、今回は1が出る」というように法則を複雑にすればするほど、その偏りが平均に近づくまでの回数はかなりの時間を要する事が分かります。(要するに複雑な予測方法は、誤りである事も簡単には検証できない。)