ベイズの定理の式を、初めて見ると「なんだか難しいな」って思ってしまうが、ここではベイズの定理を「比」という見方で、分かりやすくざっくりつかむ。豊富な図解の説明で一歩一歩進むと、モンティ・ホール問題も簡単によく理解できるよ。
※モンティ・ホール問題の解説はこちら(モンティ・ホール問題の直観的説明は間違っていることも多い)も参照にしてください。
まず例題で理解する
ベイズの定理は「ある事が起きる原因が、AとかBとか複数あるとき、AやBが原因である確率」を推測したいときに使う。
例として、次の迷惑メール問題を考えてみよう。
私に来るメールは、恋人からか、迷惑メールかのどちらかだ(ずいぶん極端だな)。メールのうち、だいたい3通に1通が恋人からのメールで(確率1/3)、残りの3通に2通は迷惑メールだ(確率2/3)。恋人からのメールの2通に1通は「愛してる」という言葉が書いてあり(確率1/2)、迷惑メールには4通に3通くらいは「愛してる」という言葉が書いてある(確率3/4)。
さてメールに「愛してる」という言葉があったときに、それが恋人からのメール、もしくは迷惑メールである確率はどのくらいか?
で、これは以下のように計算する。
メールが来たときに、
(1)「愛してる」という言葉が書かれ、なおかつ恋人からのメールである確率は
\( \frac{1}{3} \times \frac{1}{2}=\frac{1}{6} \)
(2)「愛してる」という言葉が書かれ、なおつ迷惑メールである確率は
\( \frac{2}{3} \times \frac{3}{4}=\frac{1}{2}=\frac{3}{6} \)
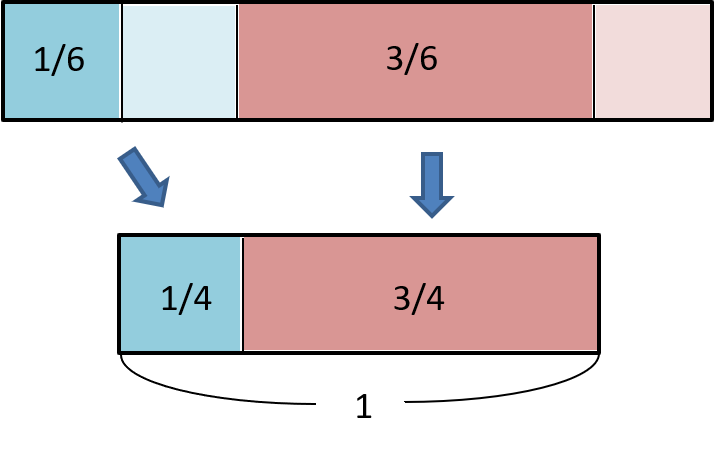
で、この確率の比を考えると1:3だから「愛してるという言葉が書かれたメール」が、恋人からのメールである確率は1/4、迷惑メールである確率は3/4だ、と考えるのがベイズの定理だ。
図で考える
確率は「面積」や「長さ」で理解するとうまく行く。「面積」が使われることが多いのだが(論文もある!⇒「面積図によるベイズ的推論の改善」)、ここでは以下のような「長さ」の図で理解してみよう。
メールが来ると、確率1/3で恋人から、確率2/3で迷惑メールである。恋人からメールが来たときに、確率1/2で「愛している」と書かれていて、迷惑メールには確率3/4で「愛している」と書かれている。これを図で表すと、以下のようになる(全体の長さを1として、確率を長さで表してゆく)。
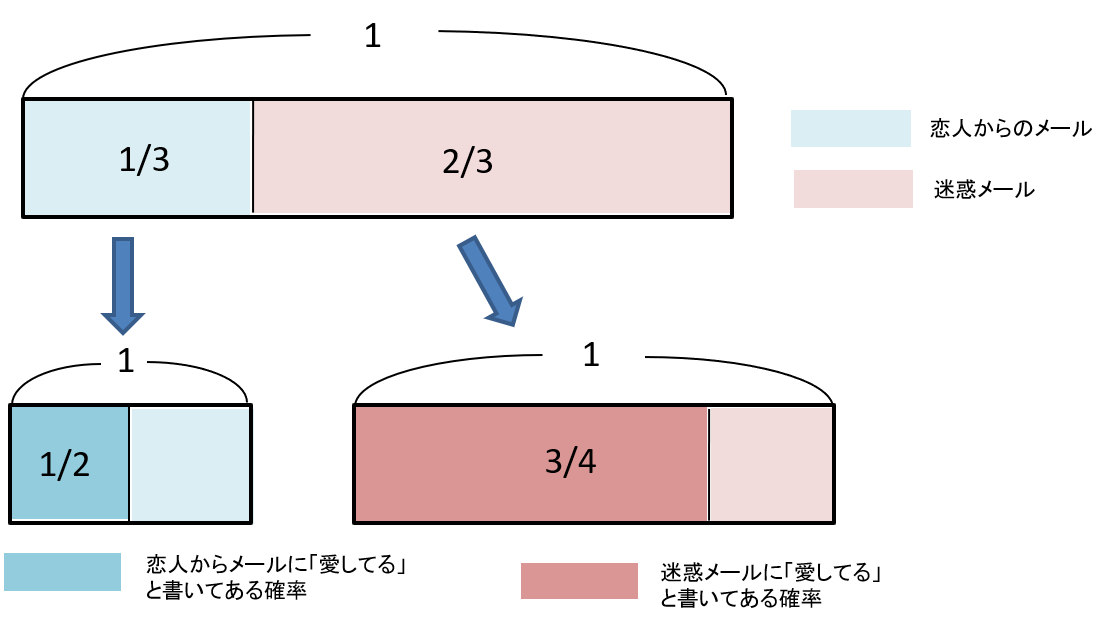
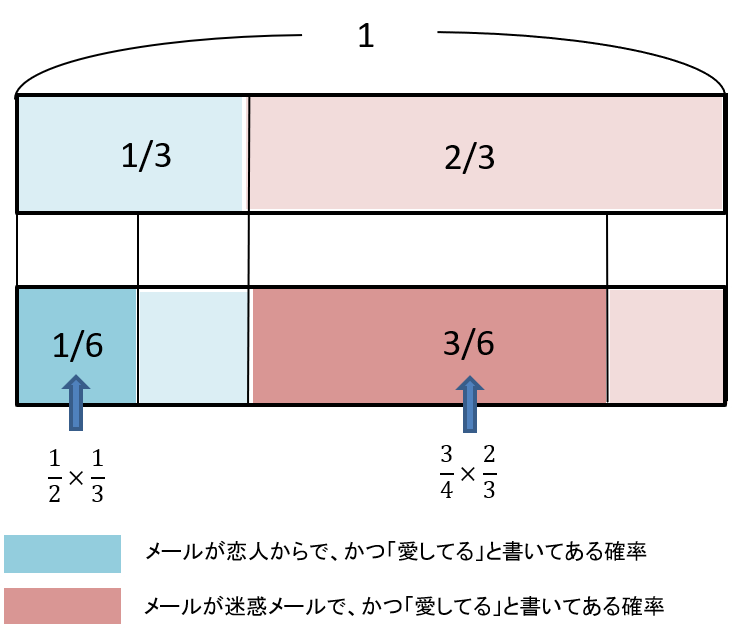
ここで、改めてすべてのことが起こる確率を1としたとき
- メールが恋人からのメールで、かつ「愛してる」と書かれているのは1/6
- メールが迷惑メールで、かつ「愛してる」と書かれているのは3/6
である。ここまでを図に表すと以下のようになる。
「愛してる」とメールに書かれているとき、それが恋人からのメールである確率と迷惑メールである確率は、上の図の濃いめの青と赤の比になる。全体を1とすると、確率は1/4と3/4になることが理解できる(下の図)。
数式で理解する
一歩進んで、数式で理解してみよう。
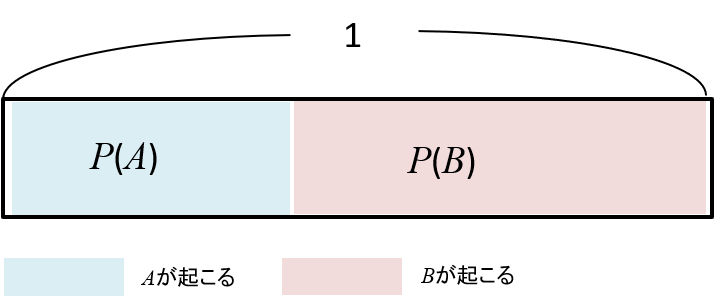
\(A\)と\(B\)という事象(原因となるもの)がそもそも起こる確率(事前確率という)を\(P(A)\)、\(P(B)\)とする。上の例だと、恋人からメールが来ることを\(A\)、迷惑メールが来ることを\(B\)とすると、\(P(A)=1/3\)、 \(P(B)=2/3\) となる。
\(A\)や\(B\)が起きたときに(それが原因で)\(X\)が起こる確率を条件付き確率と言い、\(P(X|A)\)と\(P(X|B)\)で表す。上の例だと、メールに愛してるという言葉が含まれていることを\(X\)とすれば、\(P(X|A)=1/2\)、\(P(X|B)=2/3\)である。
\(A\)と\(X\)が同時に起こる確率を\(P(X \cap A)\)とする。条件付き確率の定義から\[P(X \cap A)=P(X|A)P(A)\]が成り立つ。上の例だと\(P(X \cap A)=1/2 \times 1/3=1/6\)である。同様に\(B\)と\(X\)が同時に起こる確率を\(P(X \cap B)\)とするとこちらも\(P(X \cap B)=P(X|B)P(B)\)となる。上の例だと\(3/6\)。これを図に示すと以下のようになる。

このことから、結果\(X\)が起こったとき、原因が\(A\)である確率を\(P(A|X)\)、\(B\)である確率を\(P(B|X)\)とすると、その確率は\(P(X \cap A)\)と\(P(X \cap B)\)の比、すなわち\(P(X|A)P(A)\)と\(P(X|B)P(B)\)の比になると考えられる。例だと\(1/6\)対\(3/6\)だから、\(1/4\)と\(3/4\)になる。これを図で表すと、以下のようになる。
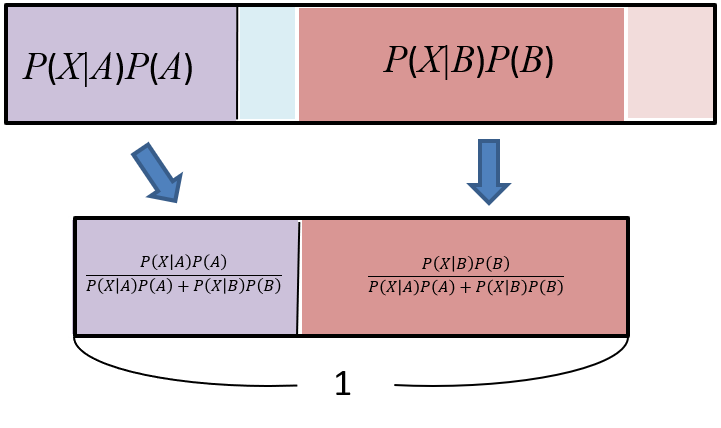
ここで、合計を1に規準化するために\[P(X|A)P(A)P(A)+P(X|B)P(B)\]で割らなければならないのである。
ベイズの定理の式と見比べてみる
ベイズの定理は\[P(A|X)=\frac{P(X|A)P(A)}{P(X|A)P(A)+P(X|B)P(B)} \tag{1}\]と書ける。例だと、「愛してる」という言葉が書かれていたときに、それが恋人からのメールである確率は、\[P(A|X)=\frac{\frac{1}{6}}{\frac{1}{6}+\frac{3}{6}}\]と計算できる。
自分がベイズの定理の式(1)を見たときに「なんか難しいな」と感じたのは、この式が「比を分数に直している」ということに気づかなかったことにある。
つまり\(x:y\)という比を分数に直すときは、合計を1にするために\(\frac{x}{x+y}\)、 \(\frac{y}{x+y}\) というように「各比の値を合計で割る」わけだ。 式(1) って分母が難しく見えるんだけど、これは比を分数に直してるもので、あんまり意識しなくてもいいのである。
改めてベイズの定理の公式(1)が、なぜ得られるかを考えてみよう。それは条件付き確率の定義が\(P(X \cap A)=P(X|A)P(A)\)であるから、 \(P(A|X) =\frac{P(X \cap A)}{P(X)}\)が成り立ち、さらに\[P(X)=P(X\cap A)+P(X \cap B)=P(X|A)P(A)+P(X|B)P(B)\tag{2}\]となる(全確率の公式と言う)ので、 \[P(A|X) = \frac{P(X \cap A)}{ P(X\cap A)+P(X \cap B) }\tag{2}\] となるわけである。
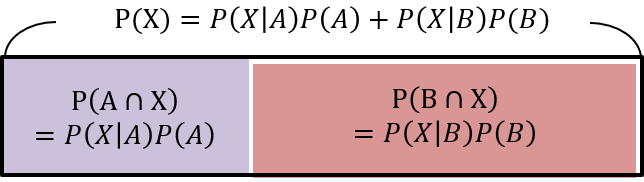
実際の多くの応用の場面では、確率の和を1に規準化しなくても、確率の比だけ使えば良いような場合も多くあり、このややこしい分母で割らなくても分子の部分、\(P(X|A)P(A)\)とか\(P(X|B)P(B)\)とかだけを使えば十分であることも多い。この部分は足して1にならないが、ざっくりと確率のようにみなせるのである。
\(n\)個で考えてみよう
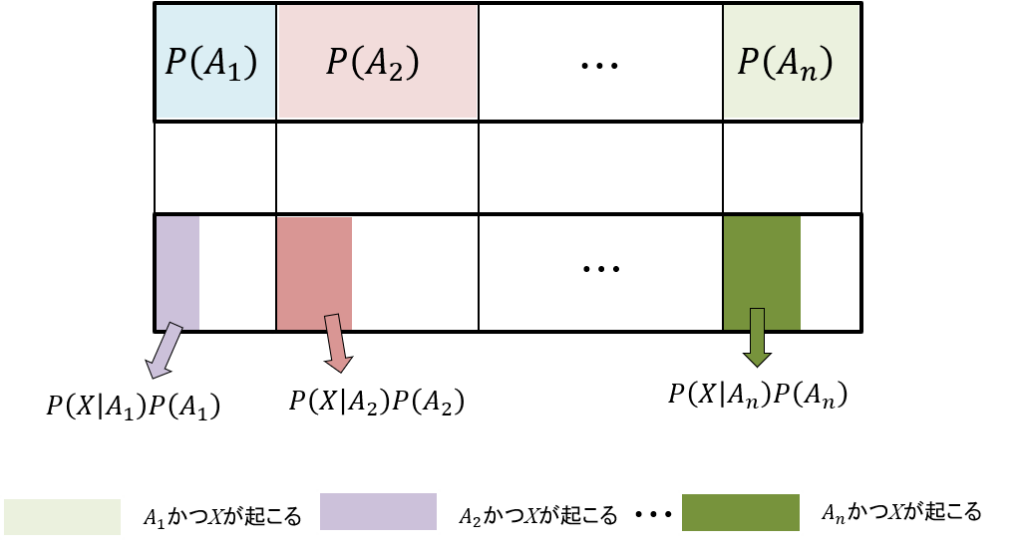
ここまでは原因となる事象が\(A\)と\(B\)の2個だけで考えていたが、\(n\)個で考えてみよう。原因となるすべての事象が\(A_1、A_2\dots 、A_n\)とあり、原因に重なりがないとする。図で表すと、以下のような感じだ。

※式で書くと、全事象を\(\Omega\)とすると、\(A_1\cup A_2\cup\dots\cup A_n=\Omega\)かつ任意の\(i\neq j\)において、\(A_i \cap A_j =\emptyset\)ということ。これを集合 \(A_1、A_2\dots 、A_n\) が \(\Omega\) の分割であるという。
このとき。原因\(A_1,A_2,\dots,A_n\)が起きて、かつ事象\(X\)が起きる確率は、それぞれ\(P(X|A_1)P(A_1),P(X|A_2)P(A_2),\dots,P(X|A_n)P(A_n)\)だ。図で表すと以下のようになる。
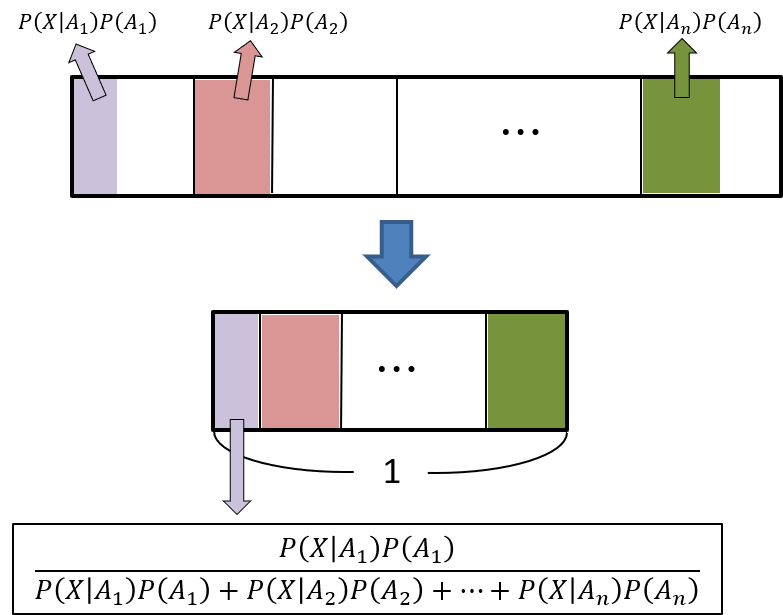
\(X\)が起きた原因が\(A_i\)である確率を考えるには、
- \(A_1\)かつ\(X\)が起きる確率:\(P(X\cap A_1)=P(X|A_1)P(A_1)\)
- \(A_2\)かつ\(X\)が起きる確率:\(P(X\cap A_2)=P(X|A_2)P(A_2)\)
- \(\cdots\)
- \(A_n\)かつ\(X\)が起きる確率:\(P(X\cap A_n)=P(X|A_n)P(A_n)\)
をすべて求めて、その全体の合計に対する 「\(A_i\)かつ\(X\)が起きる確率(\(P(X\cap A_i)=P(X|A_i)P(A_i)\)」 の割合、比を求めれば良い。
例題で考える
練習として、次の例題を考えてみよう(拙著「一歩づつゲーム理論」から)
アリス、文太、キャサリンの3人は、毎月15日にお寺に掃除に来るように、必ず1人だけ和尚に呼ばれる。(誰かは必ず呼ばれる)。3人が呼ばれる確率は、アリスが0.6、文太が0.3、キャサリンが0.1である。
3人はお寺に呼ばれて掃除をしているときに、和尚が大事にしている庭の植木鉢を壊してしまうことがある。それぞれがお寺に呼ばれているときに植木鉢を壊してしまう確率(条件付き確率)は、アリスが0.1、文太が0.4、キャサリンが0.6である。
とある15日に和尚の植木鉢が壊れていた。このとき、アリス、文太、キャサリンが割った確率(掃除に来ていた確率)をそれぞれ求めよ。誰が割った可能性が高いか?

※3人のキャクター紹介はこちら
アリス、文太、キャサリンがお寺に来ているという事象を\(A,B,C\)とし、花瓶を割るという事象を\(X\)とすると、以下の図のように考えられる。
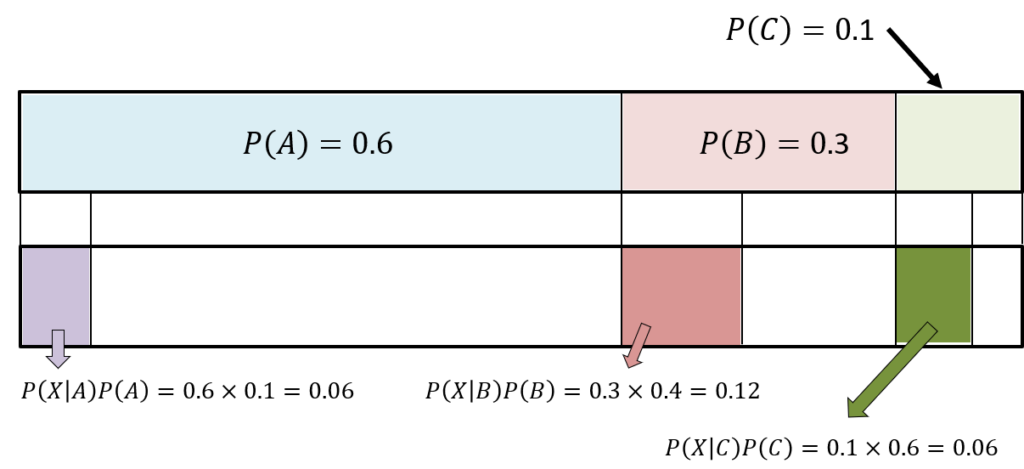
このことより「植木鉢が割れていた」という条件のもとで、アリス、文太、キャサリンが植木鉢を割った確率は、それぞれ\(1/4,1/2,1/4\)であることが分かる。
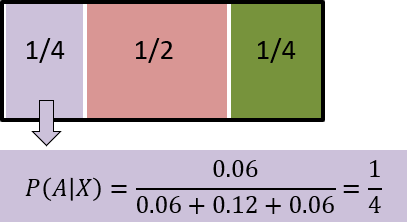
アリスはよくお寺に来るが、慎重なので植木鉢を割ることは少ない、キャサリンはお寺に滅多に来ないが、おっちょこちょいなので植木鉢をよく割る。2人が花瓶を割った確率は同じ1/4である。一番花瓶を割った確率が高いのは、そこそこお寺に来て、そこそこ植木鉢を割る文太で1/2である。
モンティ・ホール問題の場合
最後にモンティ・ホール問題を同じように図で考えてみよう。モンティ・ホール問題は以下のような問題である。(参照:モンティ・ホール問題の直観的説明は間違っていることも多い)
司会者と回答者がいて、回答者の前にはA、B、Cの3つのドアがある。1つのドアが当たりで豪華な商品があり、2つのドアはハズレである。回答者は当たりのドアを予想する。
まず、回答者がが当たりと思うドアを1つ選ぶここではAを選んだとする。司会者は、当たりのドアを知っていて、回答者が選ばなかったドアのうち、1つのドアがハズレであることを示す。ここではBのドアがハズレだと示されたとする。
司会者は、今なら回答者はCに変えても良いという。回答者はAに留まるべきか、Cに変えるべきか。
ここで、最初にA、B、Cのドアが当たる確率はすべて等しく1/3であるとし、回答者がAを指名したときに、Aが当たりの場合は、司会者は1/2でBとCのドアを開けるとする。
ここで事象を
- A:Aのドアが当たり
- B:Bのドアが当たり
- C:Cのドアが当たり
- X:(回答者がAのドアを指したときに)司会者がBのドアを開ける
とする。これまでのような図解をすると以下のようになる。
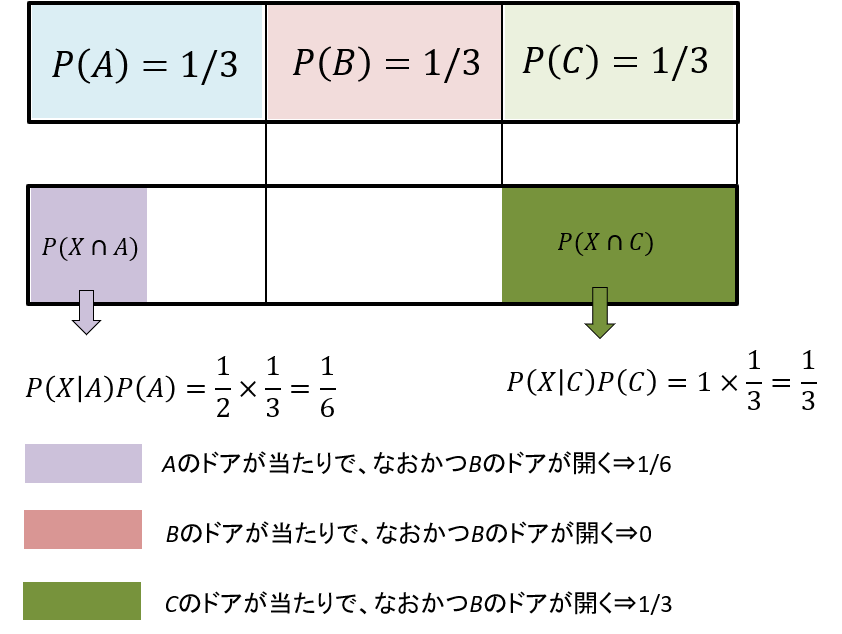
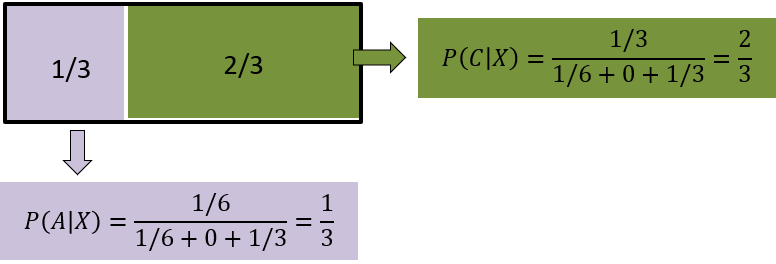
ここでBのドアが当たりで、かつBのドアが開く確率は0であることに注意をしておこう(\(P(X|B)P(B)=0\times 1/3=0 \))。
図から、司会者がBのドアを開けたなら、Aのドア(留まる)が当たりの確率(1/3)、Cのドア(変える)が当たりの確率は2/3であることが分かる。
最初の各ドアの当たる確率が異なるとき
最初に各ドアの当たる確率が異なるときについて、モンティ・ホール問題の直観的説明は間違っていることも多いで扱った。これについても図で示してみたいが、さすがに長くなりすぎるのでやめた。各自で試してもらいたい。
