支配戦略とは
戦略形ゲームにおいては、各プレイヤーがどの戦略(選択、行動、代替案)を選ぶかを決めることが分析の主たる目的となります。
このとき1人のプレイヤーに対して
自分以外のプレイヤーが何を選んでも、自分の他の戦略よりも良い戦略(利得を高くする戦略)
があれば、その戦略を(そのプレイヤーの)支配戦略と呼びます。
プレイヤーに支配戦略があれば、そのプレイヤーはその支配戦略を選ぶと考えます。
支配戦略の例
例を挙げましょう。(ゼミナールゲーム理論入門によく出てくる例ですね!)
支配戦略の例(コンビニ戦争2):2つのコンビニ、セレブ(セレブイレブン)とファミモ(ファミリーモール)が、まだコンビニがないA駅とB駅のどちらか一方に出店しようと考えている。コンビニを1日に利用する客はA駅が1200人、B駅が300人である。セレブとファミモがもし違う駅を選べば、利用客を独占できる。しかし同じ駅に出店すると、ファミモが人気で、ファミモはセレブの2倍の客数を獲得できる。すなわち両方がA駅に出店すると、セレブ400人、ファミモ800人。B駅に出店すると、セレブ100人、ファミモ200人である。ここで客数を利得と考える。セレブとファミモはどちらの駅に出店するだろうか?
ゲーム理論を持ち出すまでもなく、ちょっと考えるとセレブもファミモもA駅を選ぶことが分かるでしょう。B駅を独占しても高々300人ですからね。でも最初はこの例から始めましょう。
このゲームを利得行列で書くと下のようになります。

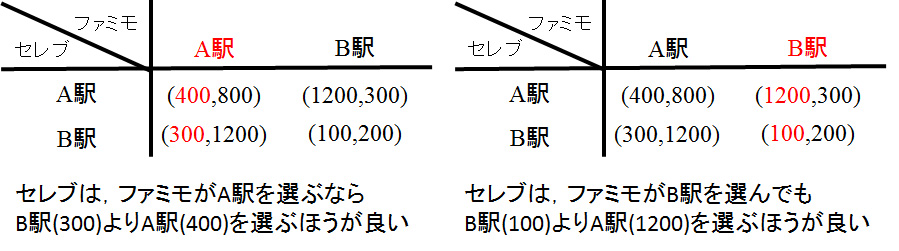
このときセレブの視点に立ってみましょう。セレブは
- ファミモがA駅を選ぶならB駅(300)よりA駅(400)を選ぶほうが良い。
- セレブは、ファミモがB駅を選んでも B駅(100)よりA駅(1200)を選ぶほうが良い。
と言うことが分かります。セレブは、ファミモが何を選んでも、B駅よりはA駅の方が良い戦略です。したがってA駅はセレブの支配戦略です(以下の図)。
同様に ファミモの視点に立って考えてみます。
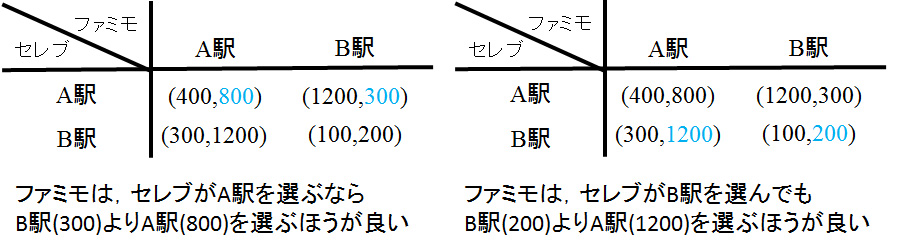
セレブは、ファミモが何を選んでも、B駅よりはA駅の方が良い戦略です。したがってA駅はセレブの支配戦略です。
もしすべてのプレイヤーに支配戦略があれば、すべてのプレイヤーが支配戦略を選ぶことがゲームの答となり、そのゲームは解けたことになると言えるでしょう。今回の例では、セレブもファミモも支配戦略はA駅でしたから、両方ともA駅を選ぶと予測でき、ゲームは解けたことになります。
支配戦略はゲーム理論における「強い解」
支配戦略は、相手の選択に関わらず、自分にとって他の選択より良いような選択がある場合です。このときプレイヤーは、相手や自分にとっての知識が完全でなくても行動を確定することができます。例えば、
(禅が好きなアリス)アリスと文太は、それぞれ禅寺に行くか、ショッピングセンターに行くか悩んでいる。アリスはとにかく禅寺に行きたいので、文太が禅寺に行っても行かなくても、ショッピングセンターよりは禅寺がいい。
この場合、アリスにとって禅寺に行くことが支配戦略になり、アリスは禅寺に行くことが確定します(だから「悩んでいる」って問題設定はおかしいんだけど)。しかも
- 文太の利得は全く分かっていない。つまりプレイヤーに支配戦略があれば、相手の行動どころか、利得さえ分からなくても、そのプレイヤーの行動は確定する。
- アリスも結果に対する好みがすべて確定しているわけではない。例えば「文太と一緒に禅寺に行くこと」と「アリスだけが禅寺に行き、文太はショッピングセンターに行くこと」のどちらが良いかは問題には定められていない(文太が好きなのか、嫌いなのか?)。つまりプレイヤーは、相手の選択それぞれに対する自分の好みだけが分かっていれば行動は確定する。
ということになります。つまり支配戦略があれば、細かい情報はなくてもプレイヤーはそれを選ぶことになります。このことは、支配戦略によるプレイヤーの行動の予測は、かなり確かなものになっているということで、支配戦略がないゲーム(その解はナッシュ均衡)よりも、より確からしい予測を与えているということになります。
- 「禅が好きなアリス」は文太の好みが分からないと、文太が何を選ぶかは分からない。この例の続きは(未完)。
- 支配戦略がない場合は、ゲームの解としてはナッシュ均衡を考えることになる。
