ナッシュ均衡（ざっくりした説明）

ここではまずナッシュ均衡について、ざっくり説明します。

ナッシュ均衡とは

ゲーム理論におけるナッシュ均衡とは、ざっくりいうと

どのプレイヤーも、自分だけでは、それ以上利得が大きくできない状態

です。「状態」って言い方は不正確過ぎるか。もう少し正確に言うと、ナッシュ均衡とは

どのプレイヤーも、他のプレイヤーがそのナッシュ均衡の戦略を選んでいるもとでは、その戦略が一番利得が高くなる（他の戦略では利得が同じか低くなる）

ような戦略の組です。あんまり変わんないか。

ナッシュ均衡の例

例を挙げましょう（これは支配戦略を説明するときに用いた例の「客数」を変えたものです）。

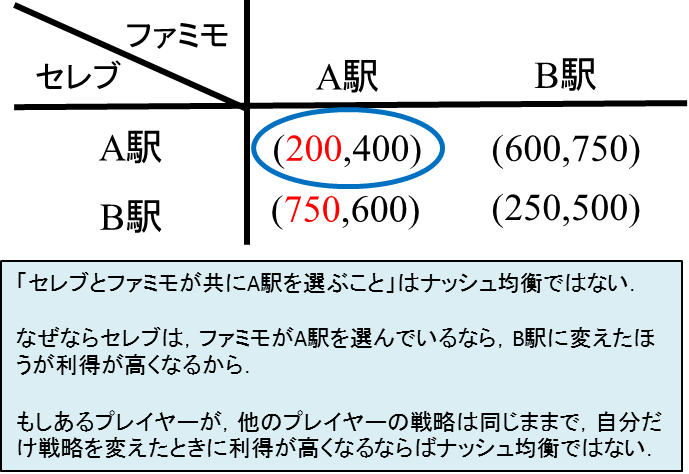
２つのコンビニ、セレブ（セレブイレブン）とファミモ（ファミリーモール）が、まだコンビニがないA駅とB駅のどちらか一方に出店しようと考えている。コンビニを１日に利用する客はA駅が600人、B駅が750人である。セレブとファミモがもし違う駅を選べば、利用客を独占できる。しかし同じ駅に出店すると、ファミモが人気で、ファミモはセレブの2倍の客数を獲得できる。すなわち両方がA駅に出店すると、セレブ200人、ファミモ400人。B駅に出店すると、セレブ250人、ファミモ500人である。ここで客数を利得と考える。セレブとファミモはどちらの駅に出店するだろうか？

このゲームを利得行列で書くと下のようになります：

例えば「セレブとファミモが共にA駅を選ぶこと」（同じ場所でお客を取り合う）はナッシュ均衡ではありません。なぜならセレブは、ファミモがA駅を選んでいるなら、B駅に変えたほうが利得が高くなるからです。このように、他のプレイヤーの戦略が変わらないもとで、あるプレイヤーが選択を変えると利得が高くなるならば、その戦略の組はナッシュ均衡ではありません。

これに対し、例えば「セレブがA駅、ファミモがB駅を選ぶこと」（違う場所で棲み分ける）はナッシュ均衡です。なぜならセレブもファミモも、相手がそれを選んでいる限り、自分の利得をもっとも高くしているからです。つまりナッシュ均衡では、

どのプレイヤーも（相手がその戦略を選んでいるならば）、それ以上利得を高くできない（他の戦略では利得が同じか低くなる）

と言うことになります。

ナッシュ均衡は2つ以上あるときもある

しかしこの例では「セレブがA駅、ファミモがB駅を選ぶこと」だけではなく、「セレブがB駅、ファミモがA駅を選ぶこと」もナッシュ均衡になることが分かります。つまりナッシュ均衡は1つとは限らず、2つ以上ある場合もあります。このときどちらをゲーム理論の解とすべきかは難しい問題で、これは「均衡選択」と呼ばれる理論と「均衡精緻化」と呼ばれる理論で考えられています（2つの違いを説明するのはちょっと難しい）これはまた別の機会に。

ナッシュ均衡が複数あるゲームの代表例は、調整ゲームとチキンゲームです。調整ゲームの記事では、どういうときにナッシュ均衡が実現しやすいかについても述べています。

ナッシュ均衡がなぜ解なのか

ナッシュ均衡以外が結果として予測されたとします。このとき、もしすべてのプレイヤーがその予測を知ったならば、少なくとも1人はその予測から違う行動を取ることで利得を高くすることができるはずです。そのプレイヤーは、ナッシュ均衡と違う行動を取るでしょうから、もはやその予測は当たりません。このことから、ゲームの結果の予測をプレイヤーが知っても結果が成り立つためには、その予測はナッシュ均衡でなければならないはずです。（じゃんけんの必勝法と行動ファイナンス・行動経済学」も参考にしてください）

ここに注意だよ

すべてのプレイヤーが支配戦略を選んでいるときはナッシュ均衡になります。これはナッシュ均衡の特殊ケースと考えられます。したがって囚人のジレンマの結果もナッシュ均衡であると言えます。
上記の点から考えると、じゃんけんにはナッシュ均衡がありませんが、確率を用いる「混合戦略」を考えるとナッシュ均衡が存在します。このような混合戦略まで考えると、すべてのn人有限ゲームにナッシュ均衡が存在します。この素晴らしい定理を誰が証明したかは、よく考えれば分かるはずである。これによって、その人はノーベル経済学賞を受賞しています。私ではありません。