ナッシュ均衡の求め方：2人ゲームの利得行列の場合

ここではゲーム理論におけるナッシュ均衡を求める方法について「プレイヤーが2人で混合戦略（確率を用いる戦略）を考えない場合」について説明します。ゲーム理論の基本中の基本と言えます。

• 混合戦略（確率を用いる戦略）のナッシュ均衡の求め方はこちら
• クールノー均衡の求め方はこちら
• ナッシュ均衡とは何かはこちら
• ナッシュ均衡の概念を理解するおけいこはこちら

ナッシュ均衡の求め方

ナッシュ均衡は「すべてのプレイヤーが最適反応戦略（利得が最も高くなる戦略）を選び合う戦略の組み合わせ」ですから、以下の方法で求めることができます。

• STEP1 プレイヤー１の立場で考える。
  • 相手（プレイヤー２）のすべての戦略に対して、プレイヤー１がもっとも利得が高くなる戦略をチェックする（プレイヤー１の最適反応戦略）。ここでは利得に下線を引く。
• STEP2 プレイヤー１の立場でチェックが終わったら、プレイヤー２の立場で考える。
  • 相手（プレイヤー１）のすべての戦略に対して、プレイヤー２がもっとも利得が高くなる戦略をチェックする（プレイヤー２の最適反応戦略）。ここでは利得に下線を引く。
• STEP3　すべてのチェックが終わったら、両プレイヤーの利得に下線が引かれているのがナッシュ均衡。（利得ではなく、戦略の組であることに注意！）

例題

以下の利得行列でナッシュ均衡を求めてみましょう。

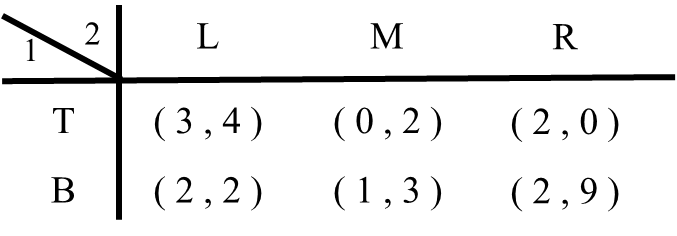
STEP1　まず、プレイヤー１の立場で考えます。相手（プレイヤー２）のすべての戦略に対して、プレイヤー１がもっとも利得が高くなる戦略（最適反応戦略）をチェックし、利得の下に下線を引いて行きます。

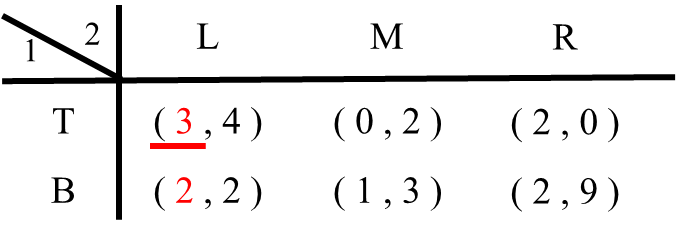
1.プレイヤー２がLという戦略を選んだ場合を考えます。プレイヤー１はTを選べば利得３、Bを選べば利得２です。したがってプレイヤー１はTを選びます（TがLに対する最適反応戦略）。そこでTを選んだ時の利得３に下線を引きます。

2. プレイヤー２がMという戦略を選んだら？プレイヤー１はTを選べば利得0、Bを選べば利得1です。したがってプレイヤー１はBを選びます（BがMに対する最適反応戦略）。そこでBの利得１に下線を引きます。

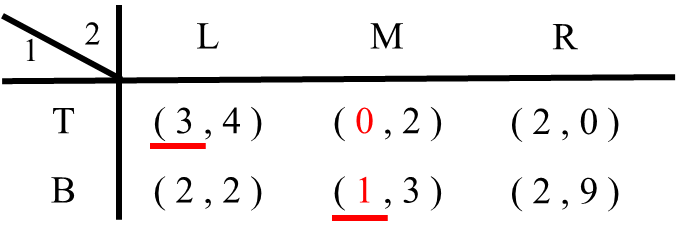
3. 最後にプレイヤー２がRという戦略を選んだ場合を考えます。プレイヤー１はTを選んでも、Bを選んでも利得は２で同じです。この場合はTとBの利得２の両方に下線を引きます（ TもBもRに対する最適反応戦略）。

STEP2　プレイヤー１に対する検討が終わったので、次にプレイヤー２の立場で考えます。相手（プレイヤー１）のすべての戦略に対して、プレイヤー２の利得がもっとも高くなる戦略（最適反応戦略）をチェックし、利得に下線を引いて行きます。

4.　プレイヤー１がTという戦略を選んだ場合を考えます。プレイヤー２はLを選べば利得４、Mを選べば利得２、Rを選べば利得０です。したがってプレイヤー２はLを選びます（LがTに対する最適反応戦略）。そこでLの利得４に下線を引きます。

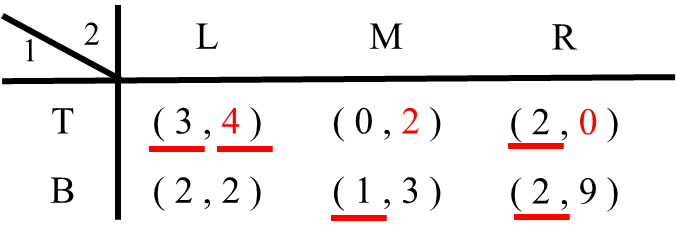
5.　最後にプレイヤー１がBという戦略を選んだ場合を考えます。プレイヤー２はLを選べば利得２、Mを選べば利得３、Rを選べば利得９です。したがってプレイヤー２はRを選びます（RがBに対する最適反応戦略）。そこでRの利得９の下に線を引きます。

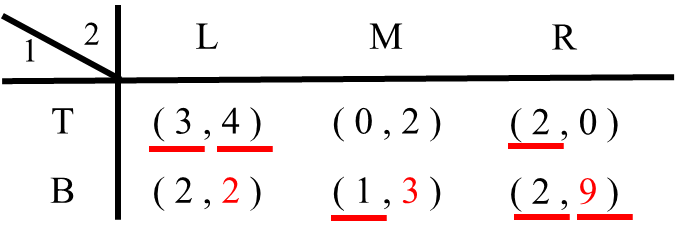
STEP３これでプレイヤー１とプレイヤー2のすべてのチェックが終わりました。プレイヤーの両方の利得に下線が引かれている戦略の組がナッシュ均衡です！「

ナッシュ均衡は「プレイヤー１はTを選び、プレイヤー２はLを選ぶ」「プレイヤー１はBを選び、プレイヤー２はRを選ぶ」の２つです。このようにナッシュ均衡は複数出てくる場合があります（これが悩みの種）。これを(T、L)と(B、R)のように、ベクトルのように書く場合もあります。

ナッシュ均衡は「戦略の組 (profile of strategies)」なので、戦略の組として答えます。「ナッシュ均衡は(3、4)と(2、9)です」などと答えては間違いです。それは利得の組ですから。「Tがナッシュ均衡」などと答えても間違いです。Tはプレイヤー１の戦略(a strategy of player 1）です。戦略の組み合わせではありません。