部分ゲーム完全均衡について、ざっくりと説明します。
部分ゲーム完全均衡(Subgame Perfect Equilibrium、 SPE)とは「ある点から後がゲーム(部分ゲーム)とみなせるときには、プレイヤーはそのゲームのナッシュ均衡を選んでいる」と考えるゲームの解です。
次のようなゲームを考えてみましょう。
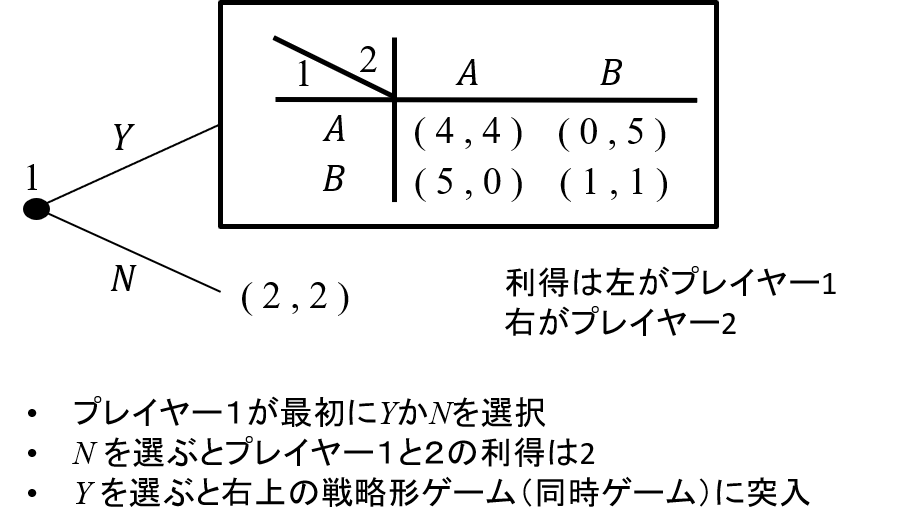
このゲームは最初にプレイヤー1がYかNかを選択。Nを選べば右上の戦略形ゲーム(同時ゲーム)に突入し、Nを選べばゲームは終了してプレイヤー1と2の利得が共に2となるゲームです。
このゲームの解はどうなると予想されるでしょう?プレイヤー1は最初の点で、Yを選んだときに、その結果がどうなるかを予想しなければなりません。右上の戦略形ゲームでは、ナッシュ均衡は(B、B)なので、プレイヤー1の利得は1になると予想されます。
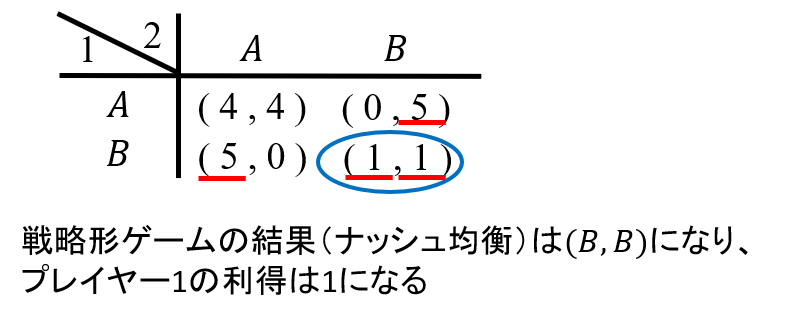
(注)
このことからプレイヤー1は最初の点でYを選べば利得は1、Nを選べば利得は2になるのでNを選ぶと考えられます。部分ゲーム完全均衡は「プレイヤー1は最初の点でYを選び、次の戦略形ゲームでプレイヤー1と2は共にBを選ぶ」となります。

部分ゲーム完全均衡を正確に学ぶには(1)展開形ゲームはどのように書けるのか(特に情報集合とは何か) (2)それを戦略形ゲームに変換するにはどうするのか、(3)展開形ゲームにおいて、ある点から後をゲーム(部分ゲーム)とみなせるのはどういうときか、を学ぶ必要があります。それはまた今度にします。今はこちらの動画を参考にしてください。
部分ゲーム完全均衡はナッシュ均衡の1つ
部分ゲーム完全均衡はナッシュ均衡の1つ(精緻化されたもの)です。例を使って、(ボンヤリとですが)説明してみましょう。
次のゲームを考えます。
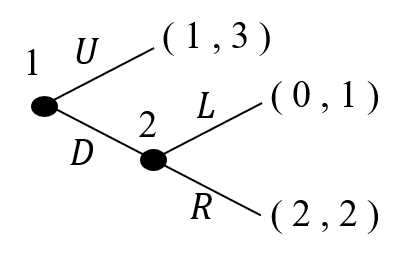
このゲームは以下のようなゲームです:
- 最初にプレイヤー1がUかDを選びます。Uを選べばゲームは終わり、プレイヤー1と2の利得は1と3になります。
- プレイヤー1がDを選ぶと、プレイヤー2がLかRを選びます。Lを選べばゲームプレイヤー1と2の利得は0と1、Rを選べばプレイヤー1と2の利得は共に2となります。
このゲームは、プレイヤー1がUかDを選び、プレイヤー2がLかRを選ぶ戦略形ゲーム(同時のゲーム)と考えることもできます。つまり、以下のような利得行列をもつ戦略形ゲームと考えることができます。

ここで「交互にプレイする展開形ゲームを、同時にプレイする戦略形ゲームに変換できるのか?」という疑問があるかと思います。確かにそこが最大のポイントですね。確かにプレイヤー2は、プレイヤー1がDを選んだのを知ってから、LかRを選ぶわけです。しかし、プレイヤー2はゲームが始まる前に「もしプレイヤー1がDを選んだらどうするか」を決めておくことはできるはずです。またプレイヤー1は、「もしDを選んだらプレイヤー2はどうするか」を推測しなければ自分の選択を決めることができません。プレイヤー1の頭の中では、プレイヤー2がどうするかは、自分が選択をする前(ゲームが始まる前)に決まっていなければなりません。このように展開形ゲームでは「すべてのプレイが行われる前に、各プレイヤーはどの点で何が選ばれるかを決定しておく」として、戦略形ゲームとして考えることができるわけです。
この戦略形ゲームのナッシュ均衡は(U、L)と(D、R)の2つです。
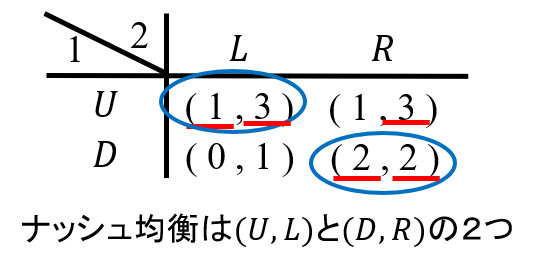
一方、このゲームの部分ゲーム完全均衡はどうなるでしょう。プレイヤー2が行動する点は部分ゲームと考えることができます。プレイヤー2はLを選べば利得1、Rを選べば利得2ですからRを選びます。このプレイヤー2の行動を推測すると、プレイヤー1はDを選びます。

(注)完全情報ゲームでは、部分ゲーム完全均衡はバックワードインダクションによる解を同じです。
均衡の精緻化
ナッシュ均衡がすべて、部分ゲーム完全均衡になるわけではありません。ここで、部分ゲーム完全均衡ではない(U、L)というナッシュ均衡が、どういうものかを展開形ゲームとして(ゲームの木で)考えてみましょう。ゲームの木では以下のようになりますね。

確かにプレイヤー2は「プレイヤー1がUを選んだと予想したときは、Lを選んでもRを選んでも利得は同じ」です。しかし、このゲームは同時のゲームではありません。予想ではなく、実際にプレイヤー1がDを選んだ場合には、プレイヤー2は、もはやLを選ばずRを選ぶでしょう。
このように展開形ゲームを戦略形ゲームに変換すると、「プレイヤーが選択した行動の情報」を考慮せずに、プレイヤーの推測を考えることになってしまうように見えます(そう見えますが、本当にそうかどうかは、難しいところです)。
そのため、変換した戦略形ゲームのナッシュ均衡をそのまま解として考えると不完全で、展開形ゲームの構造を考慮して、ナッシュ均衡の中から適切でない解を除く必要があります。これを均衡の精緻化(equilibrium refinement)と呼びます。部分ゲーム完全均衡はナッシュ均衡の精緻化による解の1つです。
まとめ
- 部分ゲーム完全均衡は「ある点から後がゲーム(部分ゲーム)とみなせるときには、プレイヤーはそのゲームのナッシュ均衡を選んでいる」と考えるゲームの解
- 部分ゲーム完全均衡はナッシュ均衡の1つ
- ナッシュ均衡から、適切でない解を取り除き、解の候補を絞り込むことを均衡の精緻化と言う
- 完全情報ゲームにおいては、部分ゲーム完全均衡はバックワードインダクションによる解になります。
東京都立大学 2020ゲーム理論1 オンライン講義(2020:コロナ対応)
- ゲーム理論2_26 不完全情報ゲームと情報集合
- ゲーム理論2_27 展開形ゲームを戦略形ゲームに変換する
- ゲーム理論2_28 部分ゲーム完全均衡とは
- ゲーム理論2_29 部分ゲーム完全均衡を求める
- ゲーム理論2_30 複数の部分ゲーム完全均衡

コメントを残す