ここでは混合戦略とは何か、混合戦略のナッシュ均衡とは何かについて記していきます。計算方法は、ここではありません。必要ならば、以下も参照してみて下さい。
- 混合戦略ナッシュ均衡の求め方（簡略版）
- ２☓２ゲームの混合戦略のナッシュ均衡の計算方法について記しています。
- ナッシュ均衡の求め方：2人ゲームの利得行列の場合
- ２人ゲームでの混合戦略ではない純粋戦略のナッシュ均衡の求め方について記しています。略
- ナッシュ均衡（ざっくりした説明）
- ナッシュ均衡とは何かについて、ざっくり記しています。
- グリコ・チョコレート・パイナップルゲームの解
ナッシュ均衡のないゲーム？
戦略形ゲームの解であるナッシュ均衡について、その考え方と2人ゲームでの求め方について書きました。しかし2人の「じゃんけん」に対してナッシュ均衡を求めると、ナッシュ均衡が存在しないように見えます。
ナッシュ均衡は「お互いが利得を最大にしている戦略の組」です。じゃんけんでは「相手がグーなら自分はパーが良い（利得を最大にする）」「自分がパーなら、相手はチョキが良い」「相手がチョキなら自分はグーが…」と循環してしまい、お互いが利得を最大にしている戦略の組はないことが分かります。（循環するからダメなわけではないんですけど、正確には…）
確認するために、ナッシュ均衡の求め方にしたがい最適反応戦略（利得を最大にする戦略）となる利得に下線を引くと以下の図になり、両プレイヤーの利得に共に下線が引かれている戦略の組はないことが分かります。
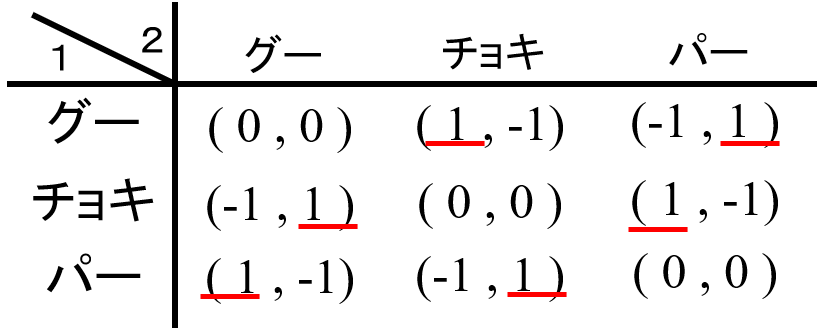
じゃんけんには戦略が３つありますが、戦略が２つであってもこのような（一見すると）ナッシュ均衡がないゲームはあります。以下のゲームは、その典型例として、よく用いられます。
（マッチングペニー）2人のプレイヤーAとBが、それぞれ表(Head)か裏（Tail）を選ぶ。2人が同じものを選べばAの勝ち、違うものを選べばBの勝ち。
このゲームは「1セント硬貨（ペニー）をお互いに持ち、同時に表か裏かを出す」というゲームから由来していることから、マッチングペニー（matching pennies。 penniesって複数形なんだ…)と呼ばれています。
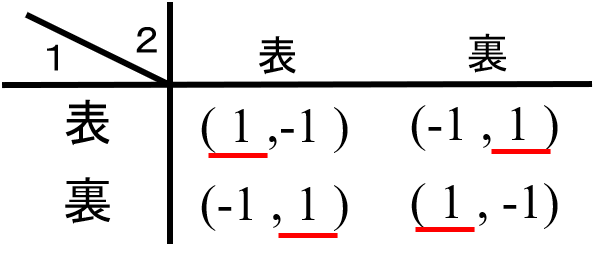
脱線しますが、日本人だと2人で順番を決めたり、勝ち負けを決めたりするときはじゃんけんをします。あっち（欧米）だとじゃんけんがなく、そのような状況では「表か裏を選ぶ」という方法を考えるのが定番のようで、ゲーム理論をやっていると頻繁に「表」「裏」を選ぶという状況が登場します。マッチングペニーが実際に行われているかどうか、私は知らないのですが（誰か教えて下さい）、テニスの試合なんかだと最初にサーブを取るかコートを選ぶかを決めるときに、一方の選手がラケットを地面に立ててぐるぐる回して放し、もう一方が落ちるラケットの上面が表か裏かを言い当てるという方法を使います（私のようなド素人だと、ラケットの表と裏が分からなくて、そこでつまづきます）。マッチングペニーに近いですが、ラケットを回すほうは自分の意志で表か裏を選択しているわけではないので「ゲーム」ではないですね。ちなみにテニスの大きな試合（ サッカー・アメフトなんかもそう）では審判がコイントスをして決めますが、これも第3者が決めているので「ゲーム」ではありません。くじと一緒です。
マッチングペニーでは、出したコインの表と裏が一致したときに、勝つプレイヤーと負けるプレイヤーをあらかじめ決めておく必要があります。これはマッチングペニーのルールがプレイヤーに対して非対称であることによります。ワタナベじゃんけんも同じで、どのような場合に誰が勝つかという、結果とプレイヤーを予め結びつけておく必要があります。戦略が２つだと対称で等確率に勝負がつくゲームは作れないのです。じゃんけんは、どのプレイヤーも勝ちの場合と負ける場合のルールが対称になっているゲーム（対称ゲーム）で、あらかじめ結果と勝者とを結びつけておく必要がありません。しかし戦略が３つ必要になります。どちらが好みでしょうか。日本人の私はじゃんけんのほうが好きですが（ラケットやペニーのような「道具」も必要なく、最初にどのようなときに誰が勝つかというプレイヤーを特定する必要もない）。じゃんけんは「あいこ」があるため勝負に時間がかかることがあります。戦略の数、必要とする道具、対称性、あいこと勝負の決定性、などを考慮するとどちらが良いかは好みで分かれるでしょう。
混合戦略
脱線してしまいましたが話を元に戻すと、マッチングペニーもじゃんけんと同様にナッシュ均衡がないように見えます。このような一見すると均衡がないゲームも、プレイヤーが確率を使って戦略や行動を選択すると考えるとナッシュ均衡が存在します。これはゲーム理論の出発点とも言える部分で、歴史的にはゲーム理論のキモと言うか核と言うか、そんな考え方なんです。
ゲーム理論では、プレイヤーが確率を用いて行動や戦略を選択することを１つの戦略とみなし、それを混合戦略(mixed strategy)と呼びます。もともと考えていた戦略を混合戦略と区別したいときは純粋戦略（pure strategy)と呼びます。純粋戦略は、確率１でそれを選ぶ混合戦略と同じと考えられるため、混合戦略は純粋戦略を含んだ考え方であると言えます（混合戦略は純粋戦略の拡張と言う方が数学的には正しいかな）。
「確率で戦略や行動を選ぶ」と言うと、「難しそうだ」「実際にそんなことあるのか」と言われそうですが、じゃんけんだと各プレイヤーが「グー・チョキ・パーを1/3ずつで選ぶ」というのが混合戦略のナッシュ均衡になります。マッチングペニーだと各プレイヤーが「表と裏を1/2ずつ選ぶ」というのがナッシュ均衡となります。そう考えると「確かに確率的に戦略を選ぶという考え方は分からないでもないな…」と思いませんか？
しかし、この混合戦略とナッシュ均衡の考え方は、なかなかの曲者で、正しく理解しにくいのです。以下では、これについて話していきます。
等確率でない場合
「確率で選ぶ」ということは「等確率で選ぶ」ことと同じではありません。以下の例を考えてみましょう。
（サッカーのPK戦のゲーム）サッカーのPK戦を簡便にしたモデルを考える。 キッカーは（キーパーから見て）ボールを左か右かのどちらかに蹴り、 キーパーは（自分から見て）左か右に飛んでゴールを阻止するとする（以下の図）。
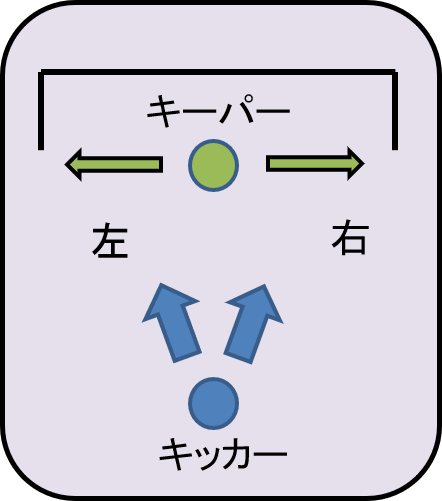
これをお互いが同時に右か左かを選ぶ戦略形ゲームと考える。 キッカーとキーパーは、違う方向に飛べばゴールの成功率は高く、同じ方向に飛べば低くなる。またキッカーは左に蹴る方が得意であり、 左のほうが成功率が高い。キッカーの利得は、ゴールの成功率、キーパーの利得は失敗率（１からゴールの成功率を引いたもの）とし、各成功率は以下のような利得行列で与えられているとする。
このようなゲームの解はどうなるだろう？
このゲームもナッシュ均衡を求めてみると、やはり（純粋戦略の）ナッシュ均衡はないことが分かります。そこで混合戦略のナッシュ均衡を求めると、
キッカーは右を5/8、左を3/8で選び、キーパーは右を7/8、左を1/8で選ぶ
となります。キッカーもキーパーも右と左を等確率で選ぶわけではありません。
どうやってこれを求めるのか？混合戦略のナッシュ均衡を求めることは、ゲーム理論の試験問題の定番です。いろんな大学のゲーム理論の講義の宿題や試験、さらには公務員試験などで出題されていて、ここを訪れた皆さんならやったことがあるか、もしくはそれを知りたくてここに来たのかもしれません。求め方は大切ですし、面白いのですけど、それは別に記すことにしましょう。
このページでは求め方ではなく、考え方について記していきますが、その前に、まず１つ重要な事実をお伝えします。上記のように一見するとナッシュ均衡がないように見えるじゃんけん、マッチングペニー、サッカーのPK問題でも混合戦略というものを考えるとナッシュ均衡がありました。実は
プレイヤーが何人いても、戦略がいくつあっても、混合戦略まで考えれば必ずナッシュ均衡は存在する
という数学の定理があるのです。凄い！凄すぎる！ナッシュ均衡は必ずあるんです（←ジョン・カビラさん風に読んで下さい、川平慈英さんでも可！）。これはゲーム理論において、たぶんいちばん重要な定理です。
この定理を証明した人は誰でしょう？賢明なあなたなら、それはもうお分かりだと思います。その人は、その功績を認められて1994年にノーベル経済学賞を取りました。
混合戦略のナッシュ均衡とは何なのか？
さてここでは求め方ではなく、上で求めた確率は「いったい何なんなのか？何の意味があるのか？」ということについて述べてみます。
専門家は、これについてハルサニーのpurification theorem(Harsanyi(1973))を考えると思いますが、ここではもう少し初心者向けの話をしてみます。
「何なんだと言われても、ナッシュ均衡でしょ？としか言いようがない！」というかもしれません。それでは以下の考え方は正しいでしょうか？
- （疑問１）キッカーは右を5/8、左を3/8で選ぶことが最適で、これに従うことが一番良いのだろうか？もし実際に自分が上のようなゲームに直面し、キッカーだったら、右を5/8で蹴ると一番良いのだろうか？
この「混合戦略のナッシュ均衡の戦略はゲームの必勝戦略で、それを出すことがプレイヤーにとっては一番いいんだ！」という考え方は正しいのでしょうか？
また、必勝戦略であるかどうかの前に、
- （疑問２）もしあなたがキッカーで5/8の確率で右に3/8の確率で蹴ろうとすると、どうやってボールを蹴るのだろうか？
という疑問もあります。疑問２は専門家には簡単なことなのでしょうが、学生に投げかけてみると、ほとんど答えられないようです。疑問１くらいだとさっぱり分かりません。
混合戦略のナッシュ均衡は求められるのに、それが何なのか分かっていないことが多い人が何と多いことか。私も成績をつける都合で宿題や試験に出しているんだということを正直に告白しなければなりません。 教員は、それに何の意味があるのか分かっていないものを、学生に求めさせていることを大いに反省しなければなりません。はい、いつか話そうと思っていました。なので、今回のこの記事は、スゴーク長くなっているのです。
まず疑問２について答えてみます。混合戦略は「確率で戦略を決定する」のですから、忠実に再現するには、何らかの「くじ」や「サイコロ」のような確率を発生させる仕組みが必要です。ゲーム理論の専門家は、これをランダムデバイス（random device）と呼びます。もし「右を5/6、左を1/6で選べ」と言われたら、「サイコロを振って1の目が出たら左、それ以外は右」を選びます。では「右を5/8、左を3/8で選べ」だと、どうすれば良いのでしょうか？このページの最後に答を記すので、皆さんで考えてみて下さい。
混合戦略のナッシュ均衡は必勝法か？
さていよいよ疑問１の「現実にゲームに直面したときに、混合戦略のナッシュ均衡に従うことは自分にとって最適なのか」ということについて考えてみます。実はこれはよく分からないんです。状況は零和ゲームか、非零和ゲームかで変わってきます。しかし私は「ざっくり言うと、必ずしもそうではない」と考えています。
それはまずじゃんけんについて考えると、分かりやすくなります。
２人じゃんけんのナッシュ均衡の戦略は「グー・チョキ・パーを1/3ずつ出す」という戦略になります。お互いに、この戦略を選んでいると、勝ち・負け・引き分けの確率は共にに1/3となります。
では仮に相手が「グーしか出さないやつ」で、そしてそれをあなたが知っていたら、あなたはどうします？このときはパーを出すことが最適です。当たり前です。そして、そうすれば、あなたは100％勝つことができます。しかし、もしあなたがナッシュ均衡の戦略である「グー・チョキ・パーを1/3ずつ出す」という戦略を選ぶとどうなるでしょう。このとき、あなたの勝つ確率は1/3になってしまいます。相手がグーしか出さないやつなのに、 あなたと相手の勝つ確率は、同じになってしまいます！
じゃんけんにおいて「グー・チョキ・パーを1/3ずつ出す」ということは最適戦略ではありません。これはナッシュ均衡の戦略でしかないのです。よくナッシュ均衡の戦略を「最適戦略」と書いている文章を見かけますが（学会発表などでもよく見られます…実は自分もそう書いてしまうことがあるのですが）、「最適」という言葉は相手の戦略が所与の場合でしか使えません。最適戦略と書かないで下さい、均衡の戦略と書いて下さい。
で？結局のところ「何なんだと言われても、ナッシュ均衡でしょ？としか言いようがない」っという所に戻って来てしまいます。つまり「混合戦略のナッシュ均衡は何を意味しているか」という問題は、そもそもの「ナッシュ均衡とは何か」という問題に立ち返ることになります。
ゲーム理論のナッシュ均衡には、いくつかの解釈があります。１つ目は「合理的なプレイヤーが、お互いがよく考えて行動を選択するとナッシュ均衡になるだろう」という考え方（伝統的なゲーム理論、合理的プレイヤーのゲーム理論）、2つ目は「プレイヤーの中で高い利得を獲得したプレイヤーだけが生き残り、そうでないプレイヤーが淘汰されるような環境で生き残っていく戦略はナッシュ均衡になるだろう」という考え方（進化ゲーム的解釈）。他に「第3者がプレイヤーにそれを推薦すると、プレイヤーはそれを選ぶだろう。それによって第3者は、自分やプレイヤー達を良い結果に導くことができる、と言う考え方もあると思いますが（メカニズムデザインなど）、あまり中心的ではないので、ここでは1つ目と2つ目の考え方に立ってみます。
１つ目と２つ目の の立場に立っても、ナッシュ均衡の戦略とは「あなたはそうすると良い、これが必勝法だ」というよりは、むしろ「プレイヤーは達はそう行動するだろうという予測」を述べているのに近いはずです。
混合戦略は確率的に行動を選択する戦略なので「プレイヤーは達はそう行動するだろうという予測」 と言っても、 1回のゲームの結果では当たっているかどうかは分かりません。サイコロで1の目が出る確率は1/6ですが、１回だけサイコロを振って出た目を見ても、その予測が正しいかどうか分からないのと同じことですよね。しかし何回も同じようなゲームが試行された場合、ナッシュ均衡の予測が当たっているかどうかを検証することができます。これについては
- 実験経済学における混合戦略の実験
- テニスやサッカーなどのスポーツの試合における実証
などがあり、いずれも混合戦略による予測は、それほど悪くはないという結果が導かれています。
まとめ
うーんかなり疲れてきたので、このへんで終わりにします。まとめると
- ナッシュ均衡がないように見えるゲームも、混合戦略のナッシュ均衡がある。必ずある。それを証明したすごい人がいる。
- 混合戦略のナッシュ均衡は最適戦略ではない。あくまでも均衡である。
- ナッシュ均衡は「そのようにプレイすることが良い」とは必ずしも言っておらず（注）、「人々はナッシュ均衡のようにプレイするだろう」と言っている。
そうは言ってもゲームにおいて「勝つために混合戦略のナッシュ均衡をうまく活用」する方法はあるはずです。 これについては、また別の機会に考えてみます。
混合戦略については、どのゲーム理論のテキストにも載っていますが、それが一体何なんだということについて書いてある本は、ほとんどないように見えます。この混合戦略のナッシュ均衡の解釈はかなり難しいからです。しかし東大の神取道宏先生は、一般向けの本などで（例えば神取（2014））このことについて言及されていて、さすがだなーと思います。
なお3/8で右、5/8で左に蹴るには、コインを3枚投げて、1枚だけ表が出たら右、それ以外（2枚表が出るか、全部表が出るか、全部裏が出る）だったら左に蹴るというのが正解です。「8本のあみだくじを引く」「八面体のサイコロを使う」なども正解でしょう。
注意点
ゲーム理論の研究者間だと混合戦略のナッシュ均衡は「ゲームの情報に僅かに不完備性があるゲームの純粋戦略均衡を考え、その不完備性がゼロに近づいたときの極限における均衡」と考えることもあります(Harsanyi (1973))。初心者向けのここではそれについては触れませんでした。
参考文献
- 神取道宏 (2014)、ミクロ経済学の力、日本評論社。
- Harsanyi, J. C.(1973) Games with randomly disturbed payoffs: A new rationale for mixed-strategy equilibrium points. Int J Game Theory 2, 1–23 . https://doi.org/10.1007/BF01737554