「高知競馬 快進撃の舞台裏」という特集のコメンテーターとして、NHK高知の制作番組「とさ金」に出演します。「競馬の経済学」を読んだディレクターから声をかけて頂きました。放送は今週の金曜6月21日19:30からの予定。高知県内だけの番組ですが、NHKプラスでは見られるようです。よろしければご覧ください!

追伸:
関連記事がこちらにあります。
追伸2:
好評につき、全国放送(7月13日(土)午前5:10-5:40)、国際放送(7月20日(土)午前5:15-5:45)でも放映されるようです。

Navigator to Game Theory
「競馬の経済学」という本を監修しました。「〇〇の経済学」というと、経済学にはあまり関係がないお金の流れが書かれている本が多いんですが、この本も類に漏れず(^^;)、気軽に読める本です(経済学者の皆さんごめんなさい)。
2022年には3兆円を超えたJRAの売上は、どのように使われるのか。競争馬は一頭いくらくらいなのか?一番賞金を稼いだ馬は?調教師の年収はいくらくらい?など、楽しく読めて、飲み会で使えそうなネタがいっぱいです!

「ゲーム理論と競馬とマーケット」など、私のコラムも3本ほど載っています。これを機会に本HPの賭けとゲームの科学の記事も増やしていきたいです。どうぞよろしくお願いします。
※本記事に対してメールを頂き、それを受けて少し書き直しました。ありがとうございました。(2024/03/16)
※修正した記事が間違ってましたので、直しました。ご指摘頂いた方、ありがとうございました(2024.03.22)
まずモンティ・ホール問題について説明しておきます。
司会者(モンティ・ホールさん)と回答者がいて、回答者の前にはA、B、Cの3つのドアがあります。1つのドアは当たりで豪華な商品があり、回答者はそのドアを当てます。2つのドアはハズレです。回答者が「当たり」のドアを当てる、というものです。
まず、回答者がが当たりと思うドアを1つ選びます。ここではAを選んだとしましょう。司会者は、当たりのドアを知っていて、回答者が選ばなかったドアのうち、1つのドアがハズレであることを示します。ここではBのドアがハズレだと示されたとしましょう。
ここで司会者が回答者に言います。「あなたには、もう一度ドアを選び直すチャンスがあります。そのままにしますか?それとも変えますか?(stick or switch?)」
今回の場合、Aのまま留まるか?Cに変えるか?ということになります。
さて、回答者はドアを変更すべきでしょうか?それとも留まるべき?
この問題、AとCの2枚のドアのうち1つが当たりなので、変えても留まっても当たる確率は半々(1/2)のように思えます。しかしこの問題の答は「変えたほうが良い」です。留まる(Aのまま)だと当たる確率は1/3、変えると(Cに変更)当たる確率は2/3になります。
なぜ、そうなるかについては、ベイズの定理を使って、数々のネットの情報や本で説明されています。拙著「ゼミナールゲーム理論入門」でも「一歩ずつ学ぶ ゲーム理論」でも、もちろん解説されています。
「お、じゃあネットで検索してみようか!」と思ったあなた!ちょっと待ってください。この問題に対して「直感的に説明すると...」とした説明には、間違っていることが結構あります。本稿の意図は「直感的な説明は間違っていることが多いので、ベイズの定理で理解しましょう」ということなんです。
特に「確率は変わらない」的な説明は、間違いです。例えば「最初に選んだドアが当たる確率は1/3、それ以外が当たる確率は2/3だから、ハズレのドアを開けた後も、最初に選んだドアの当たる確率は1/3で、それ以外が当たる確率は2/3」と言う説明は誤りです。正しい説明は「情報によって確率は変わる」です。
最初に各ドアの当たる確率が等しいと、この「確率は変わらない」という説明も(たまたま)正しいように見えるのですが、最初に当たりやすいドアと、当たりにくいドアがあると考えれば、この説明が正しくないことが分かります。
A,B,Cのドアがあり、どれか1つが当たりだとします。ただし、Aのドアは当たりやすく当たる確率は0.5、Bは当たりにくく当たる確率は0.2、Cは0.3であるとします。
回答者は最初に(当たりやすそうな)Aのドアを選んだとしましょう。
ここで司会者(解答を知っている)は、選んでないドアからハズレのドアを1つ開けます。Bのドアが当たりならCが開き、Cのドアが当たりならBが開きますね。さて、Aのドアが当たりの場合はBとCのどちらを開けても良いのですが、ここで司会者がBとCのドアを開ける確率は同じ1/2であるとします(ここを変えると答も変わります)。
さて、司会者がBのドアを開けて、ハズレであることを示したとします。回答者はドアを変えたほうが良いんでしょうか?
「最初にAのドアが当たる確率は0.5、それ以外は当たる確率は0.5、この確率は変わらない」という説明だとフィフティ・フィフティで、変えても変えなくとも確率は1/2のような気がします。
しかし、この場合はAのドアのままだと当たる確率は5/11、Cに変えると当たる確率は6/11です。この場合は、やはりドアを変えたほうが良いです。
ちなみに司会者がCのドアを開けてハズレであることを示すと、 Aのドアのままだと当たる確率は5/9、Bに変えると当たる確率は4/9です。この場合は、ドアを変えない方が良いのです。つまり、この場合は「司会者がBのドアを開けたときはCに変えたほうが良く、Cのドアを開けたときはAのドアのままが良い」です。
モンティ・ホール問題の本質は、ドアを開けたことが情報になっていて、開ける前の事前確率と開けた後の事後確率が変化している、ということにあります。なので「元の確率と変わらないから」 的な説明は間違っていることが多いのです。
A,B,Cのドアが当たる確率が、それぞれ0.54、0.13、0.33として同じ状況だとしましょう。司会者がドアを開ける前は「Aのドアが当たる確率は0.54、それ以外は当たる確率は0.46」です。司会者がBのドアを開けたとき、回答者はドアを変えたほうが良いのでしょうか?確率は変わらない」のならば「Aのドアが当たる確率は0.54」なので、変えないほうが良いですね。
しかしこの場合も「Aのドアのままだと当たる確率は0.45、Cに変えると当たる確率は0.55」になります。司会者がドアを開ける前は、Aを選んだ方が、それ以外のドアが当たる確率より高いにも関わらずです!
計算方法は、ベイズの定理を勉強してください。このように、この問題は「直感的な」理解はなかなか難しいのです。ネットの説明でも「情報によって確率は変わる」という回答を読むと良いでしょう。
認知科学や認知心理学では、なぜ人間はこの問題に対して正しい答が出せないのか、どのような点が間違いを引き起こすのかについて研究されています(いました)。興味にある方は、以下の本を参考にしてください。
市川 伸一 (著)、日本認知科学会 (編集)、確率の理解を探る―3囚人問題とその周辺 (認知科学モノグラフ 10) (1998)/5/1
ちなみに、若い頃、先輩の金融工学の大家KJ先生(川喜田二郎氏ではないよ)に「認知科学にこんな研究があります」と話したことがあります。そのときKJ先生曰く:
渡辺君。こんな研究は意味ないよ。
皆んながベイズの定理を正しく理解すれば良いだけだ!
…でした。直感的な理解ではなく、ベイズの定理で理解しましょう。
さて、この問題では「回答者が差したドアが当たりの場合は、司会者は残りの2つのドアを等しい確率で開ける」とされていました。これによって、回答者は、指さしたカーテンの中で、まだ開いていないドアに変えたほうが当たる確率が高い、となっています。
でも「司会者ができるだけ回答者に賞品を当てて欲しくない」と考えると、ドアをどのように開けると良いのでしょうか?これはゲーム理論になりますね。ゲーム理論のテキストの演習問題なんかでは、見かけるものです(私の記憶だと、たとえば「Scott Bierman and Luis Fernandez, “Game Theory with Economic Applications,” Addison Wesley, (1997)」などに載っていた気がします。)。
答はどうなるでしょうか?ベイズの定理とゲーム理論を勉強した皆さんなら簡単ですね!
朝日新聞の記事「グリコじゃんけん、いつからあった?」で、グリコじゃんけんの必勝法について、コメントしました。
本サイトのグリコ・チョコレート・パイナップルゲームのゲーム理論による解をもとに、記者さんから取材を受けたものです。
記事には、以下のデジタル版(2022年9月1日版)もありますが、有料会員しか読めないようです(^^;)
グリコじゃんけん、いつからあった?(朝日新聞)
グリコ(グリコじゃんけん)は「勝ち」と「負け」しかないのに、3点や6点の得点を割り当てて誤って計算されている答が多く、ゲーム理論として正しく解かれたものは(自分が知る限り)存在しない。ここでは 「グリコ・パイナップル・チョコレート」ゲームの正しい解について分析する。
このゲームは古くから知られていて、今でも子どもたちが遊んでいるのを見かける。多くの者の興味を引くようで、考察しているホームページや文献はいくつかあるが、どれも正しくない。…ということで、2019年度の渡辺ゼミの卒論で上野陽菜さんがこの問題に取り組んでくれたので、以下に発表。
本来は日本OR学会の2020年春季研究発表会で発表する予定であったが、コロナウィルス問題で学会が中止になったためここに公開。
結果の要旨を先にまとめると:
「グリコ・パイナップル・チョコレート」はスタート地点からじゃんけんをして、グー(以下G)で勝てば「グリコ」で3歩進み、チョキ(以下C)かパー(以下P)で勝てば「チヨコレイト」「パイナツプル」で6歩進んで、先にゴールしたほうが勝ち、というゲームである。古くから知られていて、私が子供の頃、50年くらい前には既に存在していたが、今でも子どもたちが遊んでいるのを見かける。この記事では、この「グリコ・チョコレート・パイナップル」ゲームの2人のときのゲーム理論における解を解析する。
もし、この2人ゲームの利得行列を図1の左側(進む歩数、進まれた歩数が利得)と考えるならば、ナッシュ均衡(零和ゲームなのでマキシミニ戦略と同じ)は「G,C,Pを2/5、2/5、1/5(2:2:1)で出す」ことが解になる。(求め方はいろいろなところに書いてある、例えばwikipedia) また右側と考えるならば「G,C,Pを1/4,1/2,1/4で出す」ことが解になる。
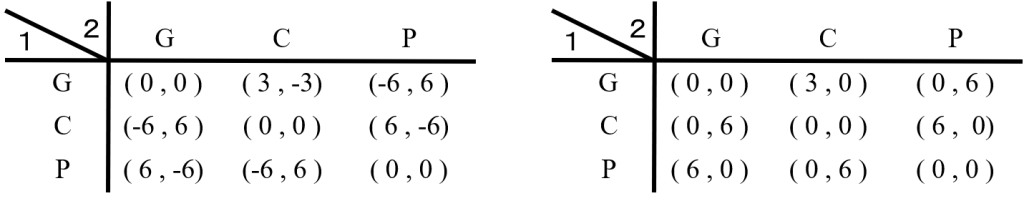
ちなみに右側は拙著「ゼミナールゲーム理論入門」に載っていて、求め方も(丁寧に)解説している。初心者にゲーム理論への興味を湧かせるために、このような例を用いたのだが、いつの間にかこの例が広まってしまった。中には「この解はおかしい」という人まで現れた。いやね、おかしいのは分かってて「このような利得だと考えると」と注意をしているのに…。失敗だった。いつか、これを正しておかなければ死ねないと、ずっと思っていた。本稿を仕上げることで、やっと死ねる。
図1のようなモデル化は間違っている。誤りの1つ目の点は、このゲームは元々「先にゴールしたほうが勝ち」というルールであり結果は「勝ち」「負け」しかなく、進んだ歩数が利得ではないからである。3とか6などの数値には正確な意味がなく、勝つか負けるかしかなく、勝ちは+1、負けは-1というゲームになるはずだ。
もう1つ上記のモデルが誤っている点、見落としている点は、このゲームは相手と自分が立っている位置によって、戦略が異なるということである。これを確認するには2人ともあと三歩以内でゴールできるという状態を想定すれば良い。このときは3歩でも6歩でもゴールできるので、G,C,Pは同じ効果を持つ(与える利得は同じ)。このときのナッシュ均衡は普通のじゃんけんと同じ「G,C,Pを1/3ずつ出す」となることは明らかだ。すなわち、このゲームにおける均衡戦略は「お互いが、あと何歩でゴールできるか」という状態に依存する。
ここではゲームを「先にゴールすれば勝ち、ゴールされれば負け」と考え、「勝てば利得が1、負ければ利得が-1」の2人零和ゲームと考える。そして2人のゴールまでの距離を状態変数としたゲーム(マルコフゲーム)と捉え、定式化して分析する。
このゲームを2人零和ゲームと考え、以下のようにモデル化する。
プレイヤー1が、あと\(n\)ステップ、プレイヤー2があと\(m\)ステップでゴールする状態を\((n,m)\)( \(1 \leq n,m \leq N\))で表す。状態\((n,m)\)で、どちらかのプレイヤーが勝つと状態が遷移し、あいこだと同じ状態に留まる。たとえば状態\((10,9)\)のとき、プレイヤー1がパーで勝てば状態\((8,9)\)に遷移する。
状態\((n,m)\)でプレイヤーが直面するゲームのナッシュ均衡(マキシミニ戦略でもある)における、プレイヤー1の期待利得(ゲームの値)を\(v_{n,m}\)とする。
\(n=0,-1\)または\(m=0,-1\)の場合にはゲームが決着し値が定まっている。これが再帰的に問題を解く初期状態となる。すなわち
\( \begin{align}
v_{0,m}=v_{-1,m}=1 & v_{n,0}=v_{n,-1}=-1 \tag{1}
\end{align} \)
(\(1 \leq n,m \leq N\))とする。
このとき状態\((n,m)\)におけるゲームのプレイヤー1の利得は、以下の表となることが分かる。
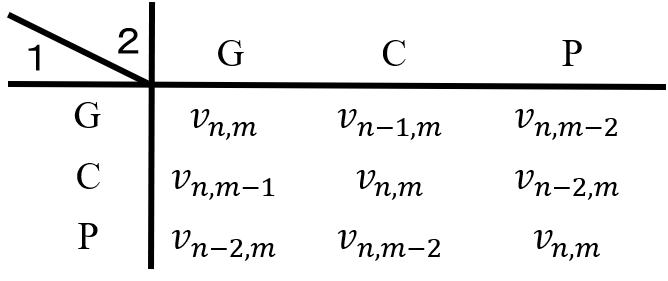
零和ゲームであることから、プレイヤー2の利得は、上記行列に-1を乗じたものとなる。
ゲーム\((n,m)\)のプレイヤー1の均衡戦略とゲームの値\(v_{n,m}\)を求める。なお、ここでプレイヤー2の戦略は、状態\((m,n)\) でのプレイヤー1の戦略と同じになる。
プレイヤー1が均衡において、G,C,Pを出す確率(混合戦略)を\(q_G,q_C,q_P\)とする。このときプレイヤー2がG,C,Pを出したときのプレイヤー1の期待利得を\(E_G,E_C,E_P\)とすると、
\( \begin{align}
E_G=q_Gv_{n,m}+q_Cv_{n,m-1}+q_Pv_{n-2,m} \\
E_C=q_Gv_{n-1,m}+q_Cv_{n,m}+q_Pv_{n,m-2} \\
E_P=q_Gv_{n,m-2}+q_Cv_{n-2,m}+q_Pv_{n,m}
\end{align} \)
となる。
ここでナッシュ均衡では
\[
E_G=E_C=E_P=v_{n,m} \tag{2}
\]
が成立する。
上記の理由を正確に説明すると長くなるため端折って説明する。このゲームには、純粋戦略のナッシュ均衡はない。そして、これから1つの戦略に確率0を割り当てる(つまり2つの戦略のみに確率を割り当てる)ような混合戦略を用いたナッシュ均衡が存在しないことも分かる。ナッシュ均衡は必ず存在するので、このゲームにはすべての戦略に正の確率を割り振るような混合戦略(完全混合戦略と呼ぶ)のナッシュ均衡しかないことが分かる。
このゲームは零和ゲームであるたm、\(E_G,E_C,E_P\)はプレイヤー2がG,C,Pを出したときのプレイヤー1の期待利得であると同時に、プレイヤー2の期待利得に-1をかけたものとなる。もし均衡において\(E_G=E_C=E_P\)でなければ、プレイヤー2はこの値が最も高くなる戦略(G,C,Pのどれか)に確率0を割り当てることが最適反応戦略となる(最も高くなる戦略が2つある場合は、2つに0を割り振る)。これは上記の完全混合戦略しかナッシュ均衡がないことに矛盾する。これから\(E_G=E_C=E_P\)が得られて、期待利得\(v_{n,m}\)もこれと等しくなることが分かる。これより式(2)を得る。
ナッシュ均衡において、正の確率が割り振られる純粋戦略の期待利得はすべて等しくなる説明はこちら(混合戦略なッシュ均衡の求め方)も参照。
式(2)に対して、式(1)を初期条件として用いて、\(q_G,q_C,q_P\)と\(v_{n,m}\)を求めることで、再帰的に期待利得\(v_{n,m}\)と均衡戦略を求めることができる。しかしこの方程式は\(v_{n,m}\)に関ずる非線形方程式(3次方程式)になるため、数値的に解くこととする。
なお\(q_G,q_C,q_P\)はプレイヤー2の均衡戦略であるが(ナッシュ均衡は、プレイヤー1の期待利得を考えることで、プレイヤー2の戦略が求められる、こちらを参照)、\(n\)と\(m\)を入れ替えてプレイヤー1の戦略を求める。
まずプレイヤー1の期待利得について、基本的な確認をしてみる。
図1は、プレイヤー2のゴールまでステップ数\(m\)を横軸に取り、プレイヤー1のゴールまでのステップ数\(n\)ごとにプレイヤー1の期待利得を示したものである(\(n=1\dots,10\))。
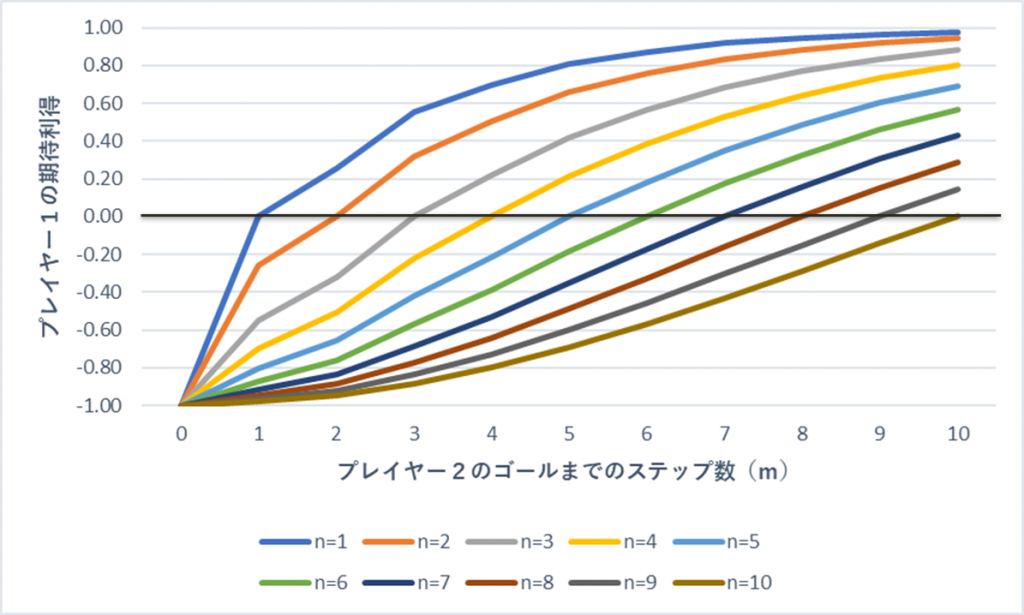
プレイヤー1の期待利得を\(v\)とするとき、プレイヤー1の勝利確率\(p\)は
\[ p=\frac{1}{2}\left(v+1\right) \]
で与えられるので、図1はプレイヤー1が勝利確率と考えることもできる。
表1はプレイヤー1の勝利確率である。例えば自分があと1ステップ(3歩)でゴールでき、相手が2ステップ(6歩)のとき((n=1,m=2))、相手はチョキかパーで勝てば逆転勝利できる位置にあるが、自分の勝利確率は63%(2/3)、相手は37%(1/3)である。
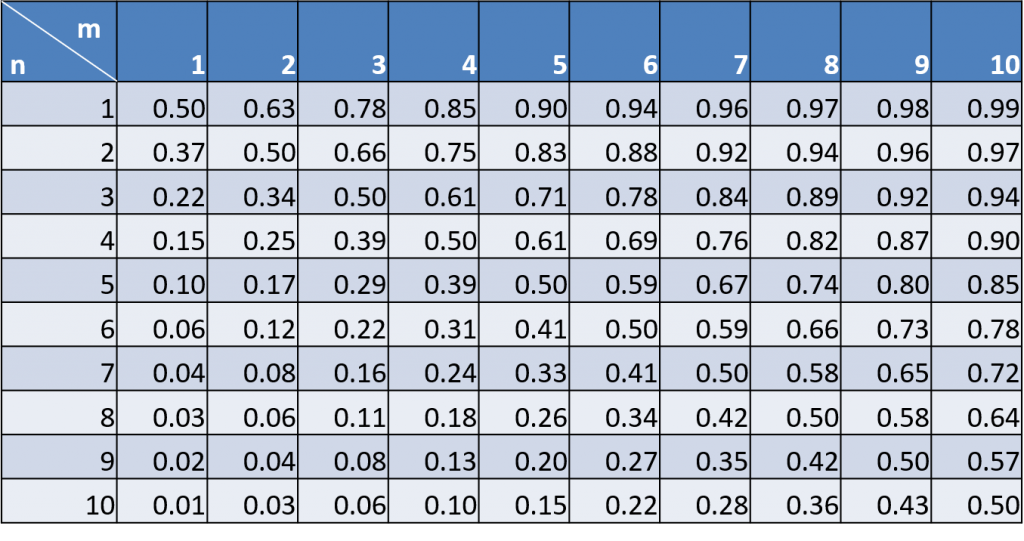
これらから、次のことが確認できる。
次に戦略について見ていこう。計算から次のようなことが分かった。
これらはたぶん均衡を求める式を丁寧に調べると証明できるのであろうが、やっていない。
さて、図2は\(m=1\)(プレイヤー2があと1ステップでゴールするとき) の両プレイヤーの戦略を、プレイヤー1の位置\(n\)を横軸としてグラフにしたものである。このゲームの特徴がよく現れている。
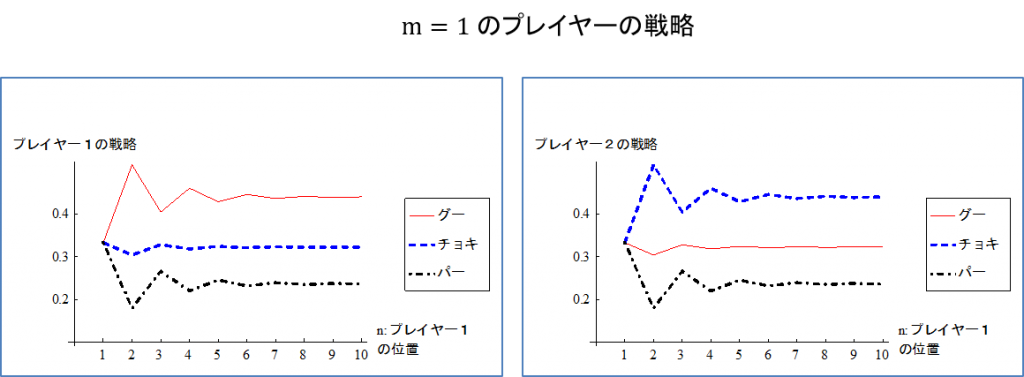
先に予想したとおり、2人ともあと1ステップでゴールできる場合( \(n=m=1\))では、G,C,Pを出す確率は\(1/3\)となり、普通のじゃんけんと同じになることが分かる。それ以外では、プレイヤー1はグーを出す確率が高く、プレイヤー2はチョキを出す確率が高い。プレイヤー2はあと1ステップでゴールできるので、グーよりもチョキやパーを出すことで有利にならないため、相手に2ステップ進ませることを何としても避けたい。そのためチョキを出してプレイヤー1がチョキやパーで進むことを阻止したいわけだ。プレイヤー1はそれを読み込むと、グーを出す確率を高くして、1ステップだけ進んでおこうとして、それが均衡となる。プレイヤー1の位置が2ステップのとき\(n=1,m=2\)では、それが最も顕著に現れ(プレイヤー2は1ステップでゴールできるにも関わらず、プレイヤー1に2ステップ進まれると逆転負けする)、プレイヤー1がグーを出す確率(=プレイヤー2がチョキを出す確率)は0.52にまで上昇する。
図3は\(m=5\)(プレイヤー2があと5ステップでゴールするとき) のグラフである。
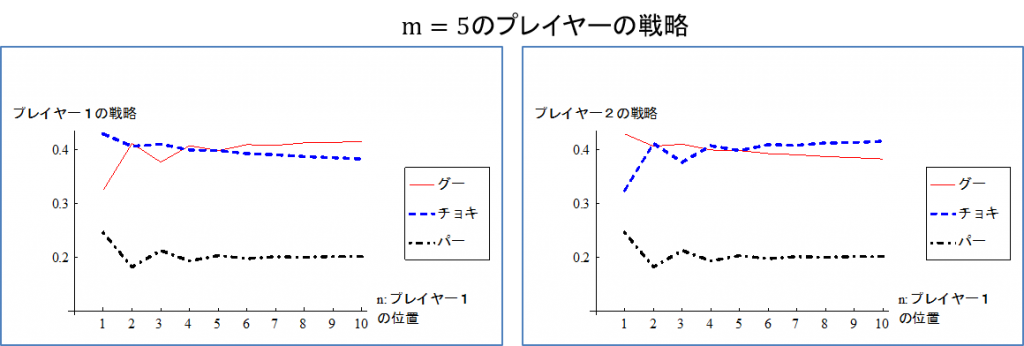
この例から分かるように、均衡戦略は次の2つの要因に影響される。
(1)ゴールまでの距離:プレイヤー1がゴールから離れるほど、グーを出す確率が増加しチョキを出す確率が減少する(プレイヤー2はチョキを出す確率が増加し、グーを出す確率が減少する)。 プレイヤー1がゴールから遠いとき、プレイヤー2はプレイヤー1が2ステップ進むことを避けるためチョキを出す確率を高め、それをプレイヤー1が読み込みグーを出す確率が高くなることを表している。相手がゴールより遠いときには逆転させないように1ステップづつ進ませる(自分がゴールから遠いときには1ステップづつ進む)戦略となる。同じ位置 \(n=m\) にいるときはグーとチョキを出す確率が同じになるので、基本的には勝っているときはチョキを出す確率が高く、負けているときはグーを出す確率が高くなる。
(2)奇数と偶数ステップの効果:プレイヤー1は偶数ステップではグーを出す確率が増加し、チョキを出す確率が減少する。先に見たようにプレイヤー1が残り2ステップでゴールする場合\(n=2\)、プレイヤー2はプレイヤー1が2ステップ進んで一気にゴールすることを阻止するためチョキを出す確率を高めるので、プレイヤー1はそれを読み込んでグーを出す確率を高める。これと同様の理由が再帰的に続くと考えられる。例えばプレイヤー1が残り3ステップと4ステップのときを考えると、どちらも1回ではゴールできず、少なくとも2回で勝たなければゴールできない。プレイヤー1が残り4ステップのとき、一気に2ステップ進まれると、残り1回で勝つチャンスがプレイヤー1に生まれるが、1ステップでは少なくともあと2回勝たなければダメなままである。これに対しプレイヤー1が残り3ステップのときは、1ステップ進んでも、2ステップ進んでも残り1回で勝つチャンスがプレイヤー1に生まれる。つまりプレイヤー2としては、プレイヤー1が偶数ステップのときに2ステップ進むことを阻止したいインセンティブが強くなる。それをプレイヤー1が読み込む結果だと思われる。
上記の2つの要因によって図3の戦略は解釈できると思われる。
最後の結果から、巷で言われる(?)図1の左側の利得行列の計算も、あながち間違っているわけではないと言える。
以上、グリコ、チョコレート、パイナップルの解をゲーム理論で解析した。なおこの確率はナッシュ均衡の確率を計算したものであり、相手がナッシュ均衡に従わない場合は必勝戦略とならないことに注意したい。例えば、チョキばかり出してくる馬鹿な相手に、上記の結果のナッシュ均衡戦略で勝負するよりは、グーを出したほうが良い。
この混合戦略のナッシュ均衡は、自分がナッシュ均衡に従っているならば、相手が何を出して来ようが、均衡における自分の期待確率を同じにしていることに注目したい。つまり自分が勝っているとき(相手よりも先に進んでいるとき)は均衡に従えば、相手が何を出そうが自分の有利さをそのまま保つことができる。これに対し、自分が負けているとき(相手が先に進んでいるとき)は均衡に従うと、相手が何を出しても自分の不利さをそのまま保つような戦略になってしまっている。そこで実践的な意味では、自分が先に進んでいるときは上記の確率に従い、負けているときは相手が均衡戦略から外れ、デタラメに出すことを期待して他の戦略を用いたほうが良いだろう。上記の偶数・奇数ステップでの知見を逆手に取り、自分が偶数ステップにいるときチョキの確率を高めて、2ステップ進む確率を高めたほうが良いかもしれない。
混合戦略のナッシュ均衡が何を意味しているのかは、混合戦略の項に少し記したが、私自身も理解していないことがいくつかある。これらは機会を見て、追加していきたい。
(以前のサイト(2010年頃)に人気が高かった記事です。内容が古くなってしまったのですが、未だにアクセスも多いようなので、再度掲載します。内容が古いことに注意してください。)
ナンバーズの番号を予測する?では「ナンバーズの当選番号の系列を見ると偏りがあって予測できそうな気になることもあるが、それは乱数や確率に対する錯覚である」という話をしました。ナンバーズの当選番号はほぼランダムで、当選番号を予測する方法はないと考えられます。しかしナンバーズでは、その当選番号を選んだ人が少なければ、当選者の賞金は多くなります。これは賭けられた金額を(主催者が控除した後に)当選者で分けるナンバーズの仕組みによるものです。したがってナンバーズでは皆が選ばない「不人気な数」を選ぶことで賞金が高くなると考えられます。賭けの分類において、ナンバーズを「勝つチャンスは完全に運によるが、利得は技術により高くなる」というクラスに分類した理由です。
ナンバーズ3のストレート(3桁の数字をその順番も含めて当てる)を例にして、人気・不人気な数を考えてみます。表1は、第41回から第600回までの560回のナンバーズのうち、いくつかの条件に当てはまる当選番号の出現回数と賞金の平均金額を表にしたものです。(最初の40回をはずしたのは、このような「くじ」は開始直後には傾向が安定しないと考えたからです。)
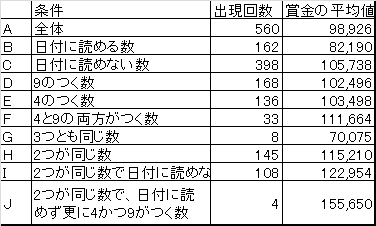
560回すべての平均賞金額は98,747円です。当選確率が1000分の1であることを考えると期待値は約99円です。ナンバーズは200円で、主催者の控除率は約50%なので、期待値はまさに理論通りであることが分かります。ちなみに、通常の宝くじも控除は約50%で、宝くじはわりに合わないギャンブルであることが分かります。
どんな数が人気・不人気なのか考えてみましょう。まずロトなどでも知られていることですが、人は誕生日や記念日などをラッキーナンバーとして選ぶことが多いようです。したがって、日付に読める数に比べ、日付に読めない数は人気がないと考えられます。例えば、私の誕生日は6月28日ですが、これに相当する628などは日付に読める数です。これに対し、一般的に下二桁が32以上の数は日付に読めません。ここで3月5日などは305と考え、035とは読まないこととしました。表を見ると、日付に読める数は平均を下回り、読めない数は平均を上回ることから、この考え方がある程度正しいことが推測されます。
またホテルの部屋番号などで分かるように、日本人は「死」を意味する4や「苦」を意味する9という数を忌み嫌う傾向にあるため、このような数も不人気と考えられます。確かに4や9がつく数も平均を上回っており、特に4と9の両方がつく数は111,664円と高い平均賞金額となります。
同じ数が3つ並ぶ数字は560回のうち8回出ていますが、いずれも賞金はぐっと低くなります。例えば第309回には777が出ていますが賞金は57,100円です。第600回までの最低賞金額は第476回の39,800円ですが、この時の当選番号は111です。ナンバーズで3つ同じ数字となる数を選ぶほど馬鹿なことはない。これに対し、同じ数が2つだけある数字の賞金は非常に高くなることが分かります。これらは人気・不人気だけではなく、ボックス・ストレートに対するナンバーズの賞金配分の仕方にも理由があるかもしれませんが、詳細は分かりません。
これらをすべて合わせて「4と9の両方がつき、同じ数が2つ並び、日付に読めない」という条件を満たす数(994,494など)を見てみると、このような数は4回出ており平均賞金額は155,650円と非常に高くなることが分かります。
ちなみに表2は第1回から600回までのナンバーズの高額賞金のベスト10です。この表を見ても「2つ同じ数があり、4か9がつき、日付に読めない」数は賞金が高いことが裏付けられます。ちなみに最高金額は第2回の988で、初期の頃の不安定さも重なって高額の当選金になっています...
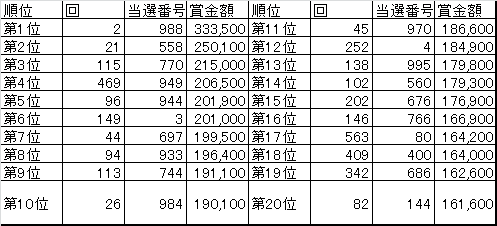
ナンバーズのちょっと良い数が分かりました。しかし残念ながらこのような不人気番号は、それが知れると皆が選ぶために人気番号となってしまいます。もう、遅いかもしれません。これについては機会をみて、もう少し考察を加えてみたいと思います。(じゃんけんに必勝法と...も参照してください)。
いやそれより、1番不人気な「2つが同じ数で日付に読めずなおかつ4か9が付く数字」を買っても期待値はかなりマイナスです.そこが問題ですよね…
このような傾向は既に知られており、「スポーツくじと宝くじの賭けの市場の効率性」,ファイナンスハンドブック 18章,今野浩・古川浩一監訳,1997、朝倉書店(私が翻訳)でも、同様の傾向が述べられています。
(参考文献)「スポーツくじと宝くじの賭けの市場の効率性」,ファイナンスハンドブック 18章,今野浩・古川浩一監訳,1997、朝倉書店。(原本はJarrow, R. A., Masksimovic, V. and Ziemba W. T. eds.,Handbooks in Operations Ressearch and Mangement Science,vol.9 Finance, Ch18.)
このサブサイト「賭けの科学」における賭けの定義を
「賭け」とは、金銭を利得とするゼロサムゲームである
とさせて頂きました。これは賭けの定義というよりは、このサイトが扱う対象の定義と考えた方が良いかもしれません。
さてこの定義を書きながら思い出したのは、東京工業大学に理財工学研究センターが設立されたときの白川浩先生の講演です。白川浩先生は、私の出身である東工大経営工学専攻の森研究室の先輩で、若くして亡くなられた研究者です。彼の研究者人生は、今野浩著「すべて僕に任せてください―東工大モーレツ天才助教授の悲劇」に壮絶に描かれているので、ぜひ読んでみてください。私が見た白川さん像は、今野先生が描くものと必ずしも一致していませんが。
白川さんは、東工大の理財工学研究センターの設立に尽力され、その設立時の中心となられました。その設立記念かなんかのシンポジウムに私は出席し、そこで白川先生は基調講演のようなことをされていました(記憶は曖昧)。白川先生が、その講演で強調されていたのは「金融工学で扱う対象はゼロサムゲームではない」ということでした...私は、この話にたいそう感銘を受け、回りを見渡したのですが、回りは皆んな「何を言っているのか、分からない」という感じでした。出席者の多くは、東工大の方、もしくは金融工学関係者の方で、経済学の方はほとんどいなかったように思えます。したがって彼が言っている意味、そして、その意図についてはほとんど理解されていないように感じました。白川先生の言葉を私なりに解釈してみると、以下のようになります。
当時、金融工学や理財工学は、ギャンブルに勝つための方法を研究していると言う人が多くおりました(今でもそうでしょうかね)。特に当時の東工大は「ものつくりこそが重要」と考えていて、金融工学という分野を東工大が扱うには反対の者が多かったと聞きます。今野先生の著書「ヒラノシリーズ」に、この話がいっぱい出てきます。「ものを作ることは経済を発展させ、人々を幸せにするが、金融工学はそうではない。個人のお金儲けのための学問ではないか、そんなものをやるのはケシカラン」と、そう考える者も多かったのです。
白川先生は「金融市場とは、限られた資金を本当に必要とする企業や生産者に回すことで経済を成長させ、皆んなが幸せになるためにあるものだ。しかし、経済や投資には不確実性があり、それによって高いリスクが投資を妨げたり、多くのお金が一瞬にして失われたりする。金融工学は、金融市場での取引におけるリスクをコントロールし、リターンを大きくすることによって、多くの人が幸せになることを目指す学問である。誰かが儲けて、誰かが損をするゼロサムゲームを扱うのではない、皆が幸せになるウインウインのノン・ゼロサム・ゲームを扱うのだ」と言いたかったのではないでしょうか。「良いものを作る」だけではなく、良いものを作るところに資金が回らなければ産業も経済も発展しない。東工大にこそ金融工学は必要なんです、と理財工学研究センターの開設にあたって、東工大の先生方にそう言いたかったんではないか、と思ったのです。
「だのにー、なぜー♪」は「若者たち」という有名な演歌の一節で、子供の頃にこの「だのにー」ってとこがすごく引っかかってました。「こんな言葉を、歌詞に使っていいのか?」と(「だのに」は、ちゃんと辞書に載っているそうです)。
白川先生の気持ちを知り、良い話をしておきながら、だのに、なぜー、私はこのサイトで、非生産的なゼロサムゲームである「賭け」について語ってしまうのでしょうか?
それは、その答はおいおい述べて行く(これから考えていく)ことにしたいと思います。
ナンバーズは物理的な機械でランダムに数が選ばれるため、競馬やTOTOなどと異なり当選番号を予測することができないと考えられます。しかし、過去の当選番号の系列を調べてみると、傾向があるように思えて番号が予測できるような気がしてきます。
このような「確率・統計上のゆらぎ」と「人間の幻想」については多くの文献が考察をしていますが、ここでは、1つの例を取りあげ、このような幻想について考えてみたいと思います。
このような傾向の中で一番単純なものは、頻度の多い数と少ない数を調べるものです。ここでは、ナンバーズ3の20回目までの当選番号において、どの数字が何回出たかを調べながら、このことを考えてみます。皆さんもここで、ナンバーズが始まって、まだ20回の時の気持ちになり、考えてみてください。
ナンバーズ3は1回の抽選で3つの数字が選ばれて、それを当てるくじです。20回までには、合計60個の数字が出現します。以下の表1には20回までの当選番号、表2には各数字の出現個数をまとめました。
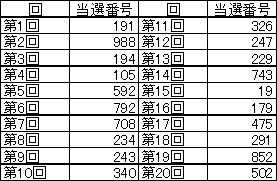
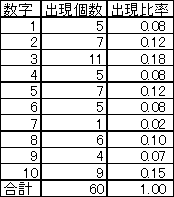
ここで20回目までの当選番号を見ると、6が1回しか出ていません。20回までには全部で60個の数字があり、平均で1つの数字は6回も出現するのはずなのに、たったの1回!これは何らかの傾向があると言わざるを得ない!という気になってきます。
まず、これはそんなに起こり得ない現象なのでしょうか?そこで10個の数から、でたらめに1つ数字が60回選ばれる時に「6」が1回以下しか出ない確率を求めてみましょう。まずはじめに「6」が1回も出ない確率を求めてみると、これは6以外の数字が60回すべて選ばれる確率であり、$$0.9^{60}=0.002$$ となります。次に「6」が1回だけ出る確率を計算するとです。合計すると「6」が1回以下しか出ない確率は$$_1 C_{60}\times 0.1 \times 0.9^{59}=0.014$$で、1.4%の確率でこのような現象が起こることが分かります。しかし、「6」に限らずに、少なくとも1つ以上の数字が1回以下しか出ない確率と考えると更に高くなるわけで(約14%)、このようなことは決して珍しい事ではないことが分かります。
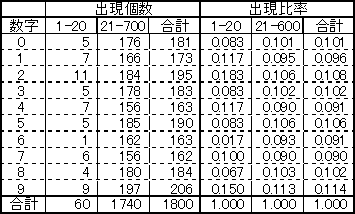
20回目以降に6が出やすいわけでも、出にくいわけでもない
20回目まで、ほとんど6は出ていない。しかもそれ以降も6の出現確率は低い。これではやっぱり6が出にくいのかと言えば、そうではありません。20回目までの6の出現比率が1.7%であったのに対して、600回目までの合計の出現比率は9.1%になり10%にぐっと近づいていることが分かります。数の出現比率が10%に近づくのは、21回目から600回目までの全体の個数が多くなり、20回目までの影響が無視できるほど小さくなったからで、6が多く出たからではないのです。6に限らずすべての数字の出現比率を見てみると、20回目まででは1.7%から18.3%と幅があるのに対し、600回目になると9.1%から11.4%と、10%の周りに近づいていることが分かります。
大数の法則から、サンプル数が多くなれば10個の数の出現比率は確率上の平均値である10%にに近づいて行きます。しかし、平均値に近づくまでにはかなりのサンプル数が必要となることが分かります。単純な数の出現比率だけでこうですから、「3が出た次の回には6が出やすい」「前々回に3が十の位に出現し、前回に9が出た場合は、今回は1が出る」というように法則を複雑にすればするほど、その偏りが平均に近づくまでの回数はかなりの時間を要する事が分かります。(要するに複雑な予測方法は、誤りである事も簡単には検証できない。)
本サブサイトで扱う「賭け」は、通常考えられているギャンブルよりは広く捉えて、「金銭を利得とするゼロサムゲームである」と定義しました(賭け・ギャンブル・ゲームの定義)。ここでは「賭け」をいくつかに分類し、それを取り扱う学問分野について考えてみます。
このサイトでは賭けを「ゼロサムゲーム」であるとしましたが、一般に賭けとは「運や不確実性を伴って利得が変化するゲーム」と考えられるでしょう。このように不確実性があるか、ないか、は賭け・ギャンブル・ゲームを分類する最大の要素であると思います。
不確実性がない賭けは、ここで「賭け」とは呼んでいるものの、一般には「ゲーム」と呼ばれることが多いでしょう。このような不確実性がない完全情報ゲーム(同時に行動することはなく、相手が何を選んだかがすべて分かるもの)は「組み合わせゲーム(combinatorial game)」や「game with no chance」などと呼ばれており、数学や計算機科学の分野で研究されています。ざっくり言うと「数学者が大好きな分野」です。参考となる書籍とページを以下に挙げておきます。
不確実性があるかないかで、学問分野は大きく分かれています。決定的な違いは「確率」が使われるかどうかです。両方を取り扱う研究者はあまりいません。なので、このサイトでは欲張って両方の話題を取り上げようと考えていますが、それでも不確実性がないゲームはやや専門外でもあり、話題は少なくなるでしょう。
これ以降では、一般に「賭け」や「ギャンブル」と言われる「不確実性のある賭け」についての分類を考えます。
Ziemba, Brumell and Schwartz (1986) はギャンブルを2つの観点から計4種類に分類しています。1つ目の観点は、「勝つチャンスが完全に運によるか、技術を要するか」のどちらであるか。もう1つの観点は「勝利による利得が、完全に運に依存するもしくは定まっている(技術によって増減しない)か、技術によって利得が増加するか」です。表にすると以下のようになります。

宝くじもナンバーズも番号はランダムに出るので、勝つチャンスは完全に運に依存していて技術を要しません。ただし、一般の宝くじの賞金は技術を持ってしても増加しませんが(そもそも、ほとんどくじを選べない)、ナンバーズやロトは、自分が選ぶ番号によって賞金を変化させる可能性があります。したがって勝利による利得の分類は、宝くじとロト・ナンバーズでは異なると言えるでしょう。ブラックジャック、ポーカー、バカラ、競馬などは技術によって勝つチャンスも利得も増加する可能性があります。右下のセルに分類されるこれらのギャンブルが、私達が一般にギャンブルと呼ぶもののほとんどを包括しています。
利得も勝つチャンスもどちらも完全に運によるものであれば、それを分析する動機は少なくなるでしょう。本サイトで扱うのは、勝つチャンスか利得の少なくとも1つが技術により増加すると考えうるものでしょう。
wikipediaの「賭博」の項目では、大谷實『新版刑法講義各論[追補版]』(成文堂、2002年)533頁を参照して「賭ける対象となる勝負事の結果に当事者として関与できるかどうか」という視点から賭博を賭事(とじ)と博戯(ばくぎ)に分類しています。
賭博とは、賭事(とじ)と博戯(ばくぎ)の二つを合わせた言葉である。賭事と博戯の違いは、賭ける側の人間が、賭ける対象となる勝負事の結果に当事者として関与できるか否かである。
賭事(とじ) – 勝負事の結果に参加者が関与できないもの
博戯 – 勝負事の結果に参加者が関与できるもの公営競技、「野球賭博」「富くじ(宝くじ)」「ルーレット」、「バカラ」などは賭事であり、「賭け麻雀」「賭けゴルフ」「賭けポーカー」などは博戯である。「クラップス」のように、一つのゲームで賭事と博戯が混在[3]する場合もある。
wikipedia「賭博」の項から
この「勝負事の結果に参加者が関与できる」ということと、(1)の「勝つチャンスや運が技術により増加する」ということは、かなり近い概念ですが、違いはあります。競馬を考えてみましょう。(1)のZeimba達の分類では、競馬はどの馬に賭けるかによって、賭けた者の当たる確率や利得を変化させることができます。(2)の分類では、競馬の結果には参加者は関与できないので、博戯になるのでしょう。
他の文献には見当たりませんが、参加者が多数か少数かは、賭けを分類するのに重要な要素であると私は考えています。
カジノなどで扱われる賭け、ブラックジャック、ルーレット、バカラなどは賭けの参加者が比較的少数です。このような問題は、確率や統計などの数学、心理学や意思決定論などがそれを取り扱う学問分野になるでしょう。
これに対し競馬などは、賭けの参加者が多数です。これを取り扱うには経済学で考える「市場」の概念が必要であると考えています。経済学・ファイナンス・金融工学などがこれを取り扱う学問分野になるのではないでしょうか。もちろん、参加者が少数である賭けを取り扱う確率や統計などの数学、心理学も必要となるため、もっとも複雑でエキサイティングな分野ではないでしょうか。本サイトでも、この分野を取り扱うことが多くなると思います。
「賭け」にはたいてい主催者がいて、それを「胴元」などと呼んだりします。カジノの主催者はオーナーで、日本の中央競馬ではJRAです(もっともJRAは執行機関であり、本当の主催者は国であるともいえますが)。宝くじの場合には、みずほ銀行を主催者と考えるよりは、自治体などを主催者と考えたほうが良いでしょう。多くの場合、法律で公認のギャンブルは公営で、ギャンブルの主催者は公的機関であったりします。
主催者の収入が運に依存するかどうか、言い換えると主催者自身がギャンブルをするかどうかは賭けを分類する重要な要因です。多くのギャンブルの主催者が公的機関であることを考えると、公的な収入が運に左右されるかどうかに対応するので、これは経済学的にも政策的にも重要な問題です。
カジノにおける多くのギャンブルでは、主催者の収入も運に依存します。例としてルーレットを考えてみましょう。アメリカンルーレットの場合、数字の数は0と00を含めて38個で、1つの数字に賭けて当たった場合の払い戻し倍率は36倍です。仮に全員が(「赤」[黒」とか「奇数」「偶数」のような賭け方ではなく)1つの数字に賭けるような賭け方をすれば、主催者の期待収入は
賭けられた金額×(38分の2)
となります。しかし、これはあくまでも期待値で、確実な収入ではありません。たまたま、参加者がルーレットの数字を次々に当てた場合は、主催者収入はマイナスになります。主催者の収入が、参加者と同様にルーレットの目に左右される点では、主催者も賭けをしていると考えられるでしょう。
カジノに対して、宝くじや日本の競馬はパリマチュアル(parimutuel)方式と呼ばれ、賭けられたお金から一定の額を控除した後、勝者にお金を配分するという方法をとっています。このような方式では主催者の収入は賭けられた金額で確定し、運には左右されません。例として、日本の競馬を考えてみましょう。日本の中央競馬では、賭けられたお金の(約)25%を主催者が控除した後、その金額を勝者に配分することになっています。主催者の収入は
賭けられた金額×25%
となります。ルーレットと異なる点は、これは確実な収入であり、本命が来ようが、穴馬が来ようが、どの馬が1着になったかには関係なく、主催者の収入は賭けられたお金にのみ依存します。ルーレットでは、主催者の収入が出た目に依存するのとは対照的に、この場合は、主催者は賭けはしていません。
ルーレットの38分の2も、日本の競馬の25%も、主催者の控除率と呼ばれるものですが、その内容は、このように少し異なります。
主催者が賭けをする方式でも、回数が多くなれば「大数の法則」に従って、収入は期待金額に近づくことが予想されます。したがって、この場合は賭けの回数が多くなることが主催者の収入を安定させるためには大切です。ルーレットにおいて、賭けられるお金の総額が1億円のときに、1億円が1回かけられるのと、100円が1万回賭けられるのでは、後者のほうが主催者には好ましく(リスクが少なく)なります。日本の競馬のようにパリマチュアルシステムでは、この2つに差はありません。
なお、日本の競馬と異なり、イギリスの競馬ではブックメーカー方式と呼ばれる主催者自身が賭けをする形もとられています。
このサブサイトは「賭けの科学」というタイトルです。そこでまず、ここで取り扱う「賭けやギャンブル」の定義について、考えなければなりません。これはなかなか難しい問題です。
一般的にギャンブルとは、「運」や「不確実性」による結果に左右され利益か損失を得る行為と考えられます。この定義では2つの問題点が生じます。1つは「賭け将棋」はギャンブルか?という問題です。昭和の初めなどでは将棋を勝負事として勝ち負けで金銭をやり取りする「賭け将棋」が行われていたと聞きます(参考:小池重明)。将棋は不確実性を持たない完全情報ゲームなので、賭け将棋まで含めると上記の定義は矛盾します。
もう1つは「投資はギャンブルか」という問題です。株式や不動産などへの投資、もっと広げて考えると会社の事業投資、研究開発投資という行為も運や不確実性を伴います。では、これはギャンブルなのかという問題です。これに対しての典型的な答は、賭けた者の期待利益が正ならば投資であり、負ならばギャンブルだ、だから株や事業への投資はギャンブルではないとするものです。一方で、個人や企業の投資も十分ギャンブルだ、とする答もあり、これは人によって見解が分かれる部分だと思います。株や不動産や事業に対する投資も期待利益が正かどうかは分かりません。私が思うには、リスクを好まず株式や不動産への投資を避けたい人はそれを「ギャンブル」と呼び、投資を好むものは「それは投資であってギャンブルではない」と呼ぶ傾向にあるように思えます。
このサイトでは主に不確実性を伴う行為について扱いますが、もう1つ将棋やオセロなどの不確実性を伴わないようなゲームについても、少しだけ考えていきたいと思います。そのような考えから、このサイトで扱う対象をうまく定義できないか考えてきました。そこで、その観点からの別の定義を考えたいと思います。それはその行為がゼロサムゲームかどうか、という観点です。一般にギャンブルと呼ばれる行為は、誰かが勝ち、誰かが負けて、そこでやり取りされる金額の合計はゼロです(ここでは参加者だけではなく、主催者・胴元の利益も含めます)。このやり取りされる金額はゼロ(生産を伴わない)という定義だと、賭け将棋は含まれ、株式・不動産などへの投資行為は含まれません。そして、この定義こそが、本サイトで扱う問題を定義することに適しているのでした。そこで、一般的な定義とは異なりますが、
このサイトにおける「賭け」とは、金銭を利得とするゼロサムゲームである
としておきます。