ここでは2☓2ゲーム(プレイヤーが2人で戦略が2つ)の混合戦略のナッシュ均衡の求め方について記します。通常は最適反応戦略のグラフを書いて求めますが、ここではグラフを書かずに簡便な方法を考えていこうと思います。以下の関連投稿も参照して下さい。
- ナッシュ均衡の求め方:2人ゲームの利得行列の場合
- 2人ゲームでの(混合戦略ではない)純粋戦略のナッシュ均衡の求め方について記しています。
- ナッシュ均衡を計算するプログラム(webアプリ)
- 混合戦略まで含めてすべてのナッシュ均衡を計算するweb上のアプリケーションです。戦略が10以下までです。
- 混合戦略
- 混合戦略と混合戦略のナッシュ均衡とは何かについて書いています。
- ナッシュ均衡(ざっくりした説明)
- ナッシュ均衡とは何かについて、ざっくり記しています。
- グリコ・チョコレート・パイナップルの正しい解
- 混合戦略の真骨頂!
- 普通、講義で学ぶ「最適反応戦略のグラフ」を書く方法は、以下のオンライン講義を参考にすると良いでしょう。
2☓2ゲームの混合戦略ナッシュ均衡を求める
以下の2☓2ゲームの混合戦略のナッシュ均衡を求めてみます。
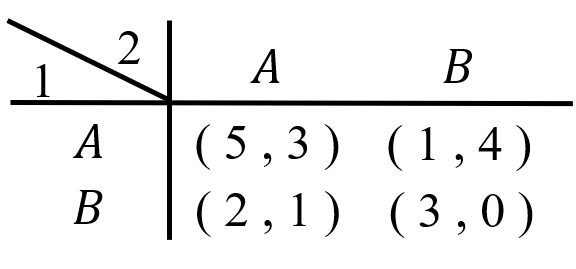
まず、プレイヤー1がAを選ぶ確率を\(p\)とします(Bを選ぶ確率は\(1-p\)となります)。次に、プレイヤー2がAを選ぶ確率を\(q\)とします(Bを選ぶ確率は\(1-q\)となります)。
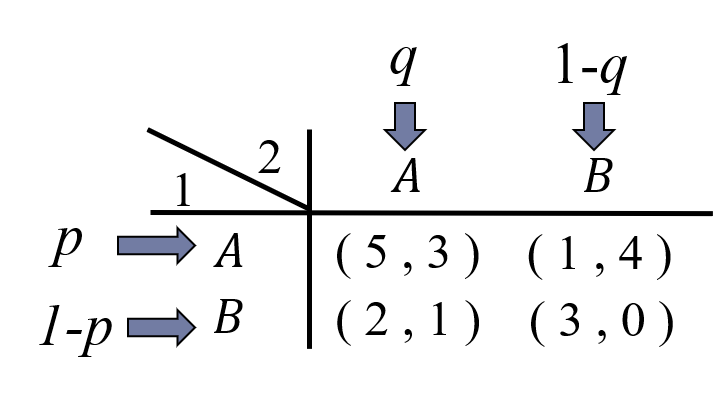
さて、プレイヤー1の戦略で\(p=1\)と\(p=0\)の混合戦略は、「Aを選ぶ」「Bを選ぶ」という純粋戦略と同等なので、ここでは求めるべきものから除外します。すなわちここでは「純粋戦略ではない混合戦略のナッシュ均衡」=「すべての戦略を選ぶ確率が正である混合戦略のナッシュ均衡」を求めることとします。したがって\(0<p<1\)とします。同様にプレイヤー2に対しても\(0<q<1\)とします。
\(0<p<1\)、\(0<q<1\) のように「すべての戦略を選ぶ確率が正である混合戦略」は完全混合戦略(completely mixed strategy) と呼ばれます。
ここでプレイヤー1が戦略Aを選んだときの期待利得(利得の期待値)は
\[ q \times 5+(1-q) \times 1=4q+1 \tag{1} \]
であり、戦略Bを選んだときの期待利得(利得の期待値)は
\[ q \times 2 +(1-q) \times 3=-q+3 \tag{2} \]
です。 完全混合戦略であるためには、期待利得が等しくなければならないので(理由は後述)
\[4q+1=-q+3\]
でなければなりません。これを解いて\(q=2/5\)を得ます。
利得の期待値の計算については後ほど詳しく説明しています。
同様にプレイヤー2を考えます。 プレイヤー2が戦略Aを選んだときの期待利得(利得の期待値)は\( p \times 3+(1-p) \times 1=2p+1 \)であり、戦略Bを選んだときの期待利得(利得の期待値)は\( p \times 4 +(1-p) \times 0=4p \)です。やはり期待利得が等しくなければならないので、\(2p+1=4p\)でなければならず、これを解いて\(p=1/2\)を得ます。
以上のことより、混合戦略のナッシュ均衡は
プレイヤー1はAを\(1/2\)、Bを\(1/2\)で選び、プレイヤー2はAを\(2/5\)、Bを\(3/5\)で選ぶ (*)
となります。
このように2☓2ゲームで混合戦略のナッシュ均衡を求めるには、各プレイヤーの2つの戦略を選んだときの期待利得が等しくなるようにすれば良いです。「なぜそうなるのか?」「ナッシュ均衡における期待利得は?」「そもそも期待利得の計算って、どうするの?」について、次に考えてみます。
均衡で期待利得が等しい理由
そもそも「期待利得(利得の期待値)」からつまずいていることも多いので、プレイヤー1の期待利得について、少し詳しく説明します。各プレイヤーが\(p,q\)に従って戦略を選んだときに、戦略の組\((A,A),(A,B),(B,A),(B,B)\)が実現する確率は\(pq,p(1-q),(1-p)q,(1-p)(1-q)\)で、そのときに実現する利得は\(5,1,2,3\)です。これより混合戦略を用いたときのプレイヤー1の期待利得は
\[ pq \times 5+p(1-q) \times 1+(1-p)q \times 2+(1-p)(1-q) \times 3 \]
となります。なお前の2項を\(p\)で、後の2項を\(q\)でくくると期待利得は
\[p(-4q+1)+(1-p)(-q+3) \tag{3} \]
と書くこともできます(この式は後で使います)。
次に「プレイヤー1がAを選んだときの期待利得」です。プレイヤー1がAを選ぶ(確率ではなく確実に選ぶ)と、プレイヤー2がAを選ぶ確率は\(q\)、Bを選ぶ確率は\(1-q\)で、そのときの利得はそれぞれ1と5ですから、期待利得は式(1)のように計算できて\(4q+1\)となります。同様にプレイヤー1がBを選ぶと期待利得は式(2)のように計算できて\(-q+3\)となるわけです。
さてこれと式(3)を見比べると、式(3)は
\[ p \times(Aを選んだときの期待利得)+ (1-p) \times
(Bを選んだときの期待利得)\]
となっていることが分かります。つまり自分がA、Bを選ぶときの確率を\(p,1-p\)としたときの期待値は「期待利得の期待値」になっている訳です。
「期待利得の期待値」が、もともとの「期待値」と同じになることは「複合くじに関する公理」と呼ばれる仮定です。ここが成立しないと考える研究も存在します。
ナッシュ均衡では、与えられた\(q\)に対して、プレイヤー1は期待利得(=式(3))を最大にする確率\(p\)を選びます(最適反応戦略)。このとき\(4q+1>-q+3\)だと\(p=1\) 、\(4q+1<-q+3\)だと\(p=0\)が式(3)を最大にすることが分かります。高い期待値を与える戦略を確率1で選ぶことが自分にとっては良く、低い期待値を与える戦略にの戦略に少しでも確率を割り当てると利得は低くなってしまうのです。
しかし\(0<p<1\)でなければなりませんので、\(p=0,p=1\)ではいけません。このことから完全混合戦略であるためには、Aを選んだときの期待利得とBを選んだときの期待利得は等しくなければならず、\(4q+1=-q+3\)でなければならないのです。プレイヤー2についても同様です。
ナッシュ均衡における期待利得を求める
以上でナッシュ均衡が\(p=1/2\)、\(q=2/5\)と計算できることが分かりました。ここで\(4q+1=-q+3=A\)と置いてみると、式(3)は
\[pA+(1-p)A=A \tag{4} \]
となります。これからナッシュ均衡における期待利得は\(A\)であることが分かります。つまり混合戦略を用いたときの期待利得は、本来は式(3)に\(p,q\)の値を代入して求めなければならないのですが、ここでは\(p\)は必要なく、\(-4q+1\)か\(-q+3\)のどちらか(簡単な方)に\(q=2/5\)を代入するだけで良いことが分かります。これよりナッシュ均衡におけるプレイヤー1の期待利得は\(-q+3=13/5\)となることが分かります。同様にプレイヤー2のナッシュ均衡における期待利得は\(4p=2\)となります。
相手の利得が自分の戦略を決める
この計算方法は、解法を鵜呑みにするのではなく、その意味を考えると「本当にこれで良いのか?」と考えこんでしまいます(よね??)。この計算方法では「相手が2つの戦略を選ぶ期待利得が等しくなるように、自分の戦略が決まる」からです。つまり端的には「相手の利得が自分の戦略を決める」「自分の利得は自分の混合戦略均衡を決めるために関係ない」ように見えるからです。
図3はここまでの例題とプレイヤー2の利得は同じであり、プレイヤー1の利得が定まっていないようなゲームです。この場合でも完全混合戦略があるとすれば、それは\(p=1/2\)となります。
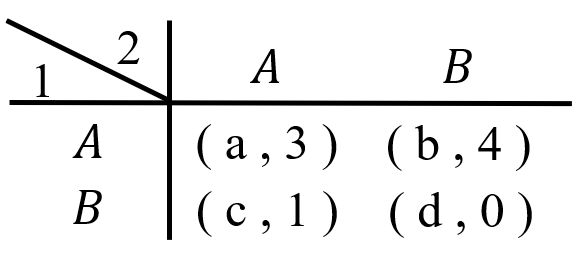
ただそれは「ナッシュ均衡でプレイヤー1が選ぶ戦略に、プレイヤー1の利得が全く関係ない」と言うわけではありません。例えば\(a=b=1,c=d=0\)では、プレイヤー1の支配戦略はAとなり、ナッシュ均衡も(A,B)となります(\(p=1,q=0\))。つまり\(a,b,c,d\)が「完全混合戦略がナッシュ均衡となるような条件」(\((a-c)(b-d)<0\)) を満たさなければなりません 。
2☓2ゲームのナッシュ均衡をすべて求める
上記の方法は2☓2ゲーム(プレイヤーが2人で戦略が2つのゲーム)の完全混合戦略のナッシュ均衡を計算する方法です。しかし、この方法ではそれ以外=「完全混合戦略ではないナッシュ均衡」は求められないため改めて注意が必要です。以下の図4の2つのゲームを見てみましょう。

図4の左側の例は図1の例題のゲームに、純粋戦略でのナッシュ均衡の求め方に従って最適反応戦略となる利得に下線を引いた図です。これから分かるように、このゲームには両プレイヤーの利得に下線が引かれる戦略の組はありません。すなわち、このゲームには、純粋戦略のナッシュ均衡がないのです。したがってこのゲームのナッシュ均衡は既に求めた完全混合戦略のナッシュ均衡が1つあるだけになります。
これに対して、図4の右側のゲームでは(A,A)(B,B)の両プレイヤーの利得に下線が引かれています。すなわちこのゲームでは(A,A)(B,B) という2つのナッシュ均衡があります。そして、さらに完全混合戦略のナッシュ均衡が1つあるのです。ここまでの方法に従って、その均衡を求めてみましょう。プレイヤー1がAを選ぶ確率を\(p\)(Bを選ぶ確率は\(1-p\))、プレイヤー2がAを選ぶ確率を\(q\)(Bを選ぶ確率は\(1-q\))とします。
プレイヤー1が戦略Aを選んだときの期待利得は\( q \times 2+(1-q) \times 0=2q\)
、戦略Bを選んだときの期待利得は\( q \times 0 +(1-q) \times 4=-4q+4\)
です。 期待利得が等しくなければならないので\(2q=-4q+4\)であることから、\(q=2/3\)を得ます。
同様にプレイヤー2を考えます。 プレイヤー2が戦略Aを選んだときの期待利得は\( p \times 3+(1-p) \times 0=3p\)で、戦略Bでは\( p \times 0 +(1-p) \times 1=1-p \)です。やはり期待利得が等しくなければならないので、\(3p=1-p\)でなければならず、これを解いて\(p=1/4\)を得ます。
これらを総合すると図4の右側のゲームのナッシュ均衡は
(1)プレイヤー1がA、プレイヤー2がAを選ぶ。(\(p=1,q=1\)に相当する )
(2)プレイヤー1がAを1/4、Bを3/4で選び、プレイヤー2がAを2/3、Bを1/3で選ぶ。
(\(p=1/4,q=2/3\)に相当する )
(3)プレイヤー1がB,プレイヤー2がBを選ぶ。(\(p=1,q=1\)に相当する )
と3つあることになります。
2☓2ゲームのほとんどのゲーム(特殊な場合を除く)は、以下の4タイプに分けることができます。
(1)2人のプレイヤーとも、支配戦略がある(囚人のジレンマなど)
(2)1人のプレイヤーだけに支配戦略がある(合理的な豚など)
(3)プレイヤーに支配戦略がなく、純粋戦略のナッシュ均衡がある(調整ゲーム、チキンゲームなど。図4の右側のゲームがこれ)
(4) プレイヤーに支配戦略がなく、純粋戦略のナッシュ均衡もない(マッチングペニー、サッカーのPKのゲームなど。図1(図4左側)のゲームがこれ)
(1)と(2)には完全混合戦略のナッシュ均衡はなく、プレイヤーが支配戦略を使う純粋戦略のナッシュ均衡が1つあるだけです。ちなみにこれに対して上記の混合戦略のナッシュ均衡の求め方を用いると\(p\)や\(q\)が負になったり、1を超えたりします。上記の求め方で0や1を超える値が出たときは、支配戦略がないかもう一度チェックする必要があります。既に見たように(3)では3個、(4)では1個のナッシュ均衡があります。
したがってナッシュ均衡をすべて求めるためには(1)-(4)に留意して求める必要があります。2☓2のナッシュ均衡の解を求める、ここで述べた方法ではなく、最適反応戦略のグラフを書く方法が一般的で、その方法を使うと(1)-(4)まで包括的(?)に求めることができます。拙著ゼミナールゲーム理論入門などを参照して下さい。
すでに話したように「混合戦略まで含めると、ナッシュ均衡は必ず存在する」という定理がありますが、さらに加えて、ほとんどの場合にナッシュ均衡は奇数個であることも証明されています。「ほとんどの場合」というのは、例えば利得が全部同じ数だったりすると、あらゆる混合戦略がナッシュ均衡になったりするわけで、そういう特殊な場合を除く、ということです。「2次方程式の解は、ほとんどの場合2個である」というのと同じような意味です(重根の場合を除いている)。
まとめ
まとめると2☓2のナッシュ均衡を求めるには
STEP.1 まず純粋戦略のナッシュ均衡を求める。
STEP.2 (1)か(2)のタイプ、すなわち支配戦略がある場合は、それで終わり。完全混合戦略のナッシュ均衡はない。
STEP.3 (3)か(4)のタイプの場合は完全混合戦略のナッシュ均衡があるので、各プレイヤーが一方の戦略を選ぶ確率を\(p,q\)とそれぞれ置き、各プレイヤーが2つの純粋戦略を選んだときの期待利得を求める。
STEP.4 上記で求めた、各プレイヤーが2つの純粋戦略を選んだときの期待利得が等しくなるように\(p,q\)を定める。相手の期待利得が等しくなるように自分の混合戦略が決まることに注意する。
となります。以上、2☓2ゲームの混合戦略のナッシュ均衡の求め方について記してみました。こうしてみると、混合戦略のナッシュ均衡とは何なのか?と考える方も多いと思います。混合戦略のページに少しそれについて書きました。
注意点
- 式(4)から分かることをもう1つ。ナッシュ均衡では、プレイヤー1はどんなpを選んでも期待利得はAになります。これはナッシュ均衡では、プレイヤー1は何を選んでも最適反応戦略(利得を最大にする戦略)になるので、果たしてナッシュ均衡戦略\((p=1/2)\)を選ぶインセンティブがあるのか?という問題が起こります。これを論じたハルサニのpurification theoremという定理があります。これは完備情報の混合戦略ナッシュ均衡は、不完備情報の純粋戦略ナッシュ均衡の極限として表現できるという定理ですが、ここでは触れていません。
参考文献
- Harsanyi, J.C. Games with randomly disturbed payoffs: A new rationale for mixed-strategy equilibrium points. Int J Game Theory 2, 1–23 (1973). https://doi.org/10.1007/BF01737554
