利得行列や数式を用いずにナッシュ均衡を理解する
ゲーム理論の解はナッシュ均衡(こちらで説明)です。「ゲーム理論が少し分かった!」と思えるためには、ナッシュ均衡が理解できていなければなりません。しかし、よくあるゲーム理論の教え方では、ナッシュ均衡は利得行列を使って説明され、プレイヤーの利得が数式や数値や表で与えられて、それを機械的に計算しナッシュ均衡を求める人が多い気がしています。
利得行列からナッシュ均衡を求める方法はこちら(ナッシュ均衡の求め方:2人ゲームの利得行列の場合)。
しかし、それで正しくナッシュ均衡の概念が理解できたと考えられるでしょうか?(いやない、反語)。ここでは、数式や表を用いない例題でナッシュ均衡を理解していきましょう。
まずナッシュ均衡の定義をおさらいしましょう。ナッシュ均衡とは、
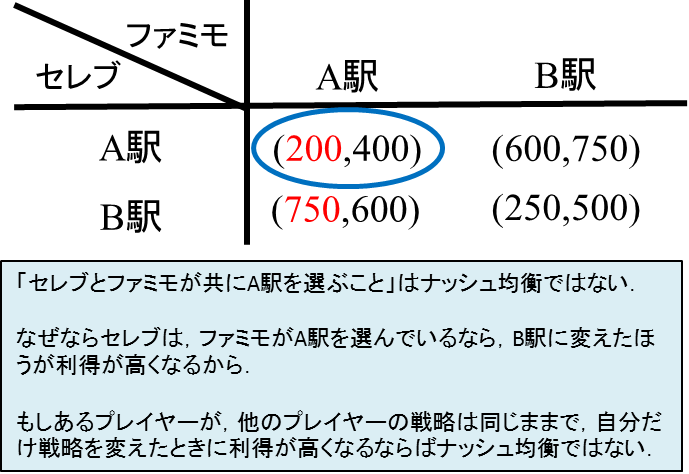
どのプレイヤーも、他のプレイヤーがそのナッシュ均衡の戦略を選んでいるならば、自分はそのナッシュ均衡の戦略を選ぶことが利得がもっとも高くなる。
です。つまり、
どのプレイヤーも、他のプレイヤーがそのナッシュ均衡の戦略を選んでいるならば、自分はそのナッシュ均衡の戦略以外を選ぶと、利得が同じか低くなる(高くなることはない)
ということです。この「同じか低くなる」と言うのは1つのポイントです。相手の戦略に対し、利得が最大になる戦略が1つならば「低くなる」で良いのですが、最大となる戦略が<同点>で2つ以上あるときは、「低くなるか同じ」 です。
なお「利得が高くなる」とは、プレイヤーにとって「良い」とか「好ましい」ということです。
2人ゲームの例
2人ゲームで練習してみましょう。なお以下では確率で戦略を選ぶ「混合戦略」は考えません。
練習1:アリスと文太は、禅寺かショッピングモールへ行く。アリスは禅が好きで、文太の行動に関わらず禅寺のほうがショッピングモールより良いと考えている。その中でどちらに行っても、文太に会えないよりは会える方が良いと考えている。一方、文太はどちらに行くかより、アリスに会えることが大切である。そして、アリスに会えたなら、ショッピングモールのほうが禅寺よりもいい。アリスに会えないときも同じである。以下から、ナッシュ均衡を選べ。複数あるときはすべて選び、ないときは「なし」と答えよ。
(A)2人とも禅寺へ行く
(B)アリスは禅寺へ、文太はショッピングモールへ行く
(C)アリスはショピングモールへ、文太は禅寺へ行く
(D)2人ともショッピングモールへ行く
正解は(A)。(A)では、どちらのプレイヤーも、自分だけが行動を変えると利得が小さくなるのでナッシュ均衡です。(B)では文太は禅寺へ行ったほうが利得が高くなりますし、(C)と(D)では、アリスは禅寺へ行ったほうが利得が高くなります。したがってナッシュ均衡ではありません。
なお(C)で「文太はショッピングモールに行ったほうが利得が高くなるのでナッシュ均衡ではない」としても良いです。「ナッシュ均衡ではない」ことを示すには、選択を変えると利得が高くなるプレイヤーが1人でもいることを示せば良いので、アリスと文太の両方について言わなくても、どちらか1人で良いわけです。なお上記の場合、アリスにとって禅寺に行くことは支配戦略です。支配戦略がある場合は、ナッシュ均衡では必ずその戦略が選ばれます。
次はどうでしょうか?
練習2:アリスと文太は、禅寺かショッピングモールへ行く。アリスも文太も、お互いのことが大好きで、どちらに行くかよりも、相手に会えるほうが大切である。ただし、アリスは、会えたときも会えないときも、禅寺のほうがショピングモールよりも良く、文太はショッピングモールのほうが禅寺よりも良い。以下から、ナッシュ均衡を選べ。複数あるときはすべて選び、ないときは「なし」と答えよ。
(A)2人とも禅寺へ行く
(B)アリスは禅寺へ、文太はショッピングモールへ行く
(C)アリスはショピングモールへ、文太は禅寺へ行く
(D)2人ともショッピングモールへ行く
正解は(A)か(D)。2人が会えている(A)と(D)では、どちらか一方だけが行動を変えると、そのプレイヤーの利得が小さくなるのでナッシュ均衡です。(B)と(C)で、どちらか一方だけが行動を変えると、そのプレイヤーの利得が高くなるのでナッシュ均衡ではありません
さてさて、次はどうでしょうか?
練習3:アリスと文太は、禅寺かショッピングモールへ行く。アリスは文太が大好きで、どこに行くかよりも文太に会えることが大切。そして、その中で会えても会えなくても、禅寺のほうがショピングモールよりも良いと考えている。文太は残念ながらアリスが嫌いで、どこに行くかよりもアリスに会わないほうが会えるより絶対良いと考えている。その中で、会えたときも会えないときも、禅寺よりショピングモールのほうが良い。以下から、ナッシュ均衡を選べ。複数あるときはすべて選び、ないときは「なし」と答えよ。
(A)2人とも禅寺へ行く
(B)アリスは禅寺へ、文太はショッピングモールへ行く
(C)アリスはショピングモールへ、文太は禅寺へ行く
(D)2人ともショッピングモールへ行く
この場合はナッシュ均衡は「なし」です。2人が会えている(A)と(D)では、文太が行動を変えると会えなくなって利得が高くなり、2人が会えていない(B)と(C)では、アリスが行動を変えると高くなるので、どれもナッシュ均衡ではありません。(なおこのような場合も確率で戦略を選ぶ混合戦略を用いると、ナッシュ均衡がありますが、その場合は利得を数値で表さなければ確率が計算できません)。
3人以上のゲームの例
ナッシュ均衡についての理解が深まってきたでしょうか?それでは3人以上の例を考えて、練習してみましょう。まず簡単な「多数決」を考えてみましょう。
練習4:(奇数人での多数決) 5人で「海」か「山」を選ぶ。 多い人数が選んだ方を選ぶと勝ち、少ない人数が選んだ言葉を選ぶと負け。当然、勝つほうが負けるより良いとします。以下から、ナッシュ均衡を選べ。複数あるときはすべて選び、ないときは「なし」を選べ。
(A) なし
(B) 全員が「海」を選ぶ
(C) 4人が「海」、1人が「山」を選ぶ
(D) 3人が「海」、2人が「山」を選ぶ
(E) 2人が「海」、3人が「山」を選ぶ
(F) 1人が「海」、4人が「山」を選ぶ
(G) 全員が「山」を選ぶ
正解は(B)と(G)です。 全員が同じ言葉を選ぶ(B)と(G)では、どの人も他者の選択はそのままで自分の選択を変えると利得が低くなるので、ナッシュ均衡です。それ以外では、少数派になっているプレイヤーは、他者の選択がそのままのときに自分の選択だけを変えると多数派となり、利得が高くなるので、ナッシュ均衡ではありません。
では、次はどうでしょう。ライアーゲームの最初に出てくる「少数決」です。少数派になったほうが勝ちです。
練習5:(奇数人の少数決) 5人で「海」か「山」を選ぶ。少ない人数が選んだ方を選ぶと勝ちで、 多い人数が選んだ方を選ぶと負け。以下から、ナッシュ均衡を選べ。複数あるときはすべて選び、ないときは「なし」を選べ。
(A) なし
(B) 全員が「海」を選ぶ
(C) 4人が「海」、1人が「山」を選ぶ
(D) 3人が「海」、2人が「山」を選ぶ
(E) 2人が「海」、3人が「山」を選ぶ
(F) 1人が「海」、4人が「山」を選ぶ
(G) 全員が「山」を選ぶ
正解は(D)と(E)です。それ以外では、多数派になっている人は、自分だけの選択を変えると少数派となり利得が高くなりますので、ナッシュ均衡ではありません。
これに対し(D)と(E)では、すべてのプレイヤーが自分だけ選択を変えても利得が高くならない(同じか低くなる)のでナッシュ均衡です。なぜかと言うと、少数派となったプレイヤーは自分の選択を変えると多数派になり利得が下がりますし、多数派のプレイヤーは自分だけが選択を変えても、やはり多数派になってしまい(多数派が変わってしまいます)利得は同じになります。
もうお腹いっぱいでしょうかね?それでは、最後の問題です。
練習6:(7人じゃんけん)7人でじゃんけんをします。もちろんすべてのプレイヤーは、勝ち、あいこ、負けの順に良い(利得が高い)とします。
(A) なし
(B) 7人ともにグーを出す
(C) 3人がグー、4人がパーを出す
(D) 1人がグー、2人がパー、4人がチョキを出す
(E) 2人がグー、2人がパー、3人がチョキを出す
(F) 3人がグー、2人がパー、2人がチョキを出す
答えは(E)と(F)です!(B)「7人ともにグーを出す」や (C)「3人がグー、4人がパーを出す」では、グーの人がパーに変えることで負けから勝ちに転じて利得が高くなります。また(D)「1人がグー、2人がパー、4人がチョキ」では、グーの人がチョキに手を変えると、アイコから勝ちに転じて利得が高くなります。したがってナッシュ均衡ではありません。しかし(E)と(F)の場合は、どの人も自分だけが手を変えても、あいこからあいこになるだけで利得は高くなりません。したがって、(E)と(F)はナッシュ均衡です。