完全情報展開形ゲームとその解き方であるバックワードインダクション(backward induction)について「展開形ゲームとは?ゲームの木とは?」で、ざっくりと話しました。ここではバックワードインダクションによるゲームの解き方を、もう少し詳しく説明します。
バックワードインダクションでゲームを解く
バックワードインダクションは完全情報展開形ゲームの解き方です。各プレイヤーは自分よりあとに行動するプレイヤーの行動を先読みし、自分の利得を最大にするように行動を選ぶのでした。
これを言い換えるとゲームは「時間的に後から行動するプレイヤーの行動から順番に解いてゆく」ということになります(有限時間の場合)。後から帰納的に(順番に)解くという意味でバックワードインダクションと呼ばれるのです。
バックワードインダクション(backward induction)は翻訳すると「後向き帰納法」「後向き遡及法」などと翻訳されるのですが、しっくりこないんでカタカナ語で書いたりすることが多いです。
具体的には、次のようにゲームを解いていきます。
1。最後のプレイヤー、つまり「そのプレイヤーが何を選んでもゲームが終わる」ようなプレイヤーの行動を求めます。そのプレイヤーは、自分が行動を選ぶと自分の利得が決まるので、そのプレイヤーが自分の利得を最大にする行動を決定することができます。
2。既に行動を求めたプレイヤーの直前に行動するプレイヤーの中から、<そのプレイヤー以降に行動するプレイヤーの行動がすべて決まっているプレイヤー>の行動を求めます。そのプレイヤーは、自分が行動を選ぶと、それ以降のプレイヤーの行動が決まっている(か、またはゲームが終わる)ために利得が決まるので、利得を最大にする行動を決定することができます。
3。2を繰り返して行き、一番最初のプレイヤーの行動が求められたら終わり…です。
例題
いくつかの例題を見てみましょう。説明をするためには、ゲームの木の点に名前がついていると便利ですので、そうしておきます。(正確には意思決定点にラベルを付けておきます。ゲームの木を少し詳しく説明!も参照してください。)
(例1)まず最初は「展開形ゲームとは?ゲームの木とは?」で説明した<コンビニ立地ゲーム>の例(図1)を、バックワードインダクションの手順の観点から、もう一度解いてみます。
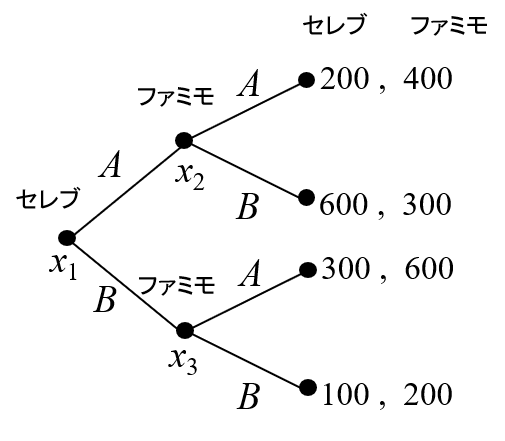
1。最後に行動するプレイヤーは、\(x2\),\(x3\)で行動するファミモなので、そこでの行動を決めます。 \(x_2\)では、ファミモはAを選べば利得が400、Bを選べば利得が300となのでAを選びます。 \(x_3\)では、ファミモはAを選べば利得が600、Bを選べば利得が200なのでAを選びます。こうして最後に行動するプレイヤーの行動が決まります。
2。次に、既に行動を求めたプレイヤーの直前に行動するプレイヤーは\(x_1\)で行動するセレブだけなので、そこでの行動を決めます。\(x_1\)では、セレブは、Aを選ぶと(ファミモがAを選ぶので)利得が200、Bを選ぶと(ファミモがAを選ぶので)利得が300となるのでBを選ぶ、というように行動が決定できます。これで最初のプレイヤーまで遡って行動が決まったので、おしまいです(図2)。
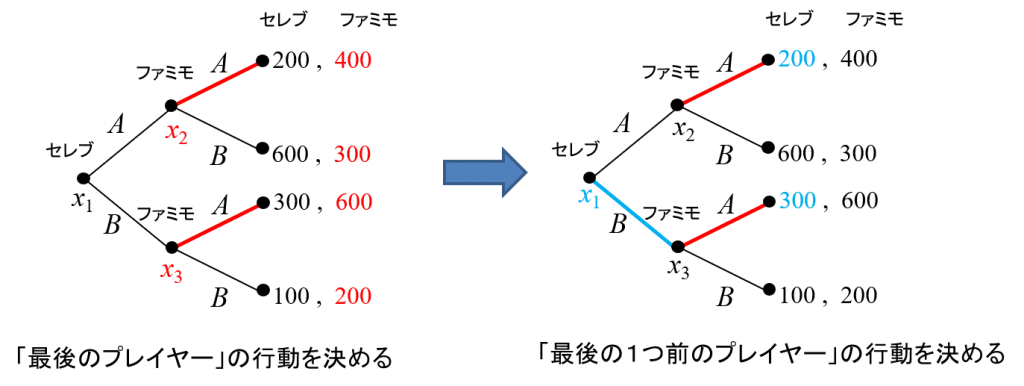
(例2)もう少し複雑な例を考えてみましょう(図3)。今度は3人のゲームです。
図3はプレイヤー1,2,3の3人からなる、以下のようなゲームです。

- はじめにプレイヤー1が\(x_1\)で\(A\)か\(B\)を選びます。
- もしプレイヤー1が\(A\)を選んだときは、プレイヤー3が\(x_2\)で\(C\)か\(D\)を選び、ゲームは終わります。
- プレイヤー1が\(B\)を選んだときは、プレイヤー2が\(x_3\)で\(E\)か\(F\)を選びます。\(E\)を選ぶと、そこでゲームが終わります。
- プレイヤー2が\(F\)を選ぶと、\(x_4\)でもう一度プレイヤー1の手番となり、プレイヤー1は\(G\)か\(H\)を選び、そこでゲームが終わります。
図3において、各点の上の数字は行動するプレイヤーを表しています。ゲームが終わったときの利得は、常に左からプレイヤー1、2、3の順になっています。
このゲームを、バックワードインダクションの手順に従い解いてみましょう。
1。最後に行動するプレイヤー(そのプレイヤーが何を選んでもゲームが終了するプレイヤー)の行動です。このゲームでは\(x_2\)で行動するプレイヤー3と、\(x_4\)で行動するプレイヤー1なので、そこでの行動を決めます。 \(x_2\)では、プレイヤー3は\(C\)を選べば利得が1、\(D\)を選べば利得が0なので\(D\)を選びます。\(x_4\)ではプレイヤー1は\(G\)を選べば利得が6、\(H\)を選べば利得が1なので\(G\)を選びます。こうして最後に行動するプレイヤーの行動が決まります。
2。次に、<そのプレイヤー以降に行動するプレイヤーの行動がすべて決まっているプレイヤー>は、\(x_2\)で行動するプレイヤー2なので、そこでの行動を決めます。\(x_2\)でプレイヤー2は、\(E\)を選ぶと利得が5、\(F\)を選ぶと(プレイヤー1がGを選ぶので)利得が4、となるので\(E\)を選ぶ、ということになります。(図4)
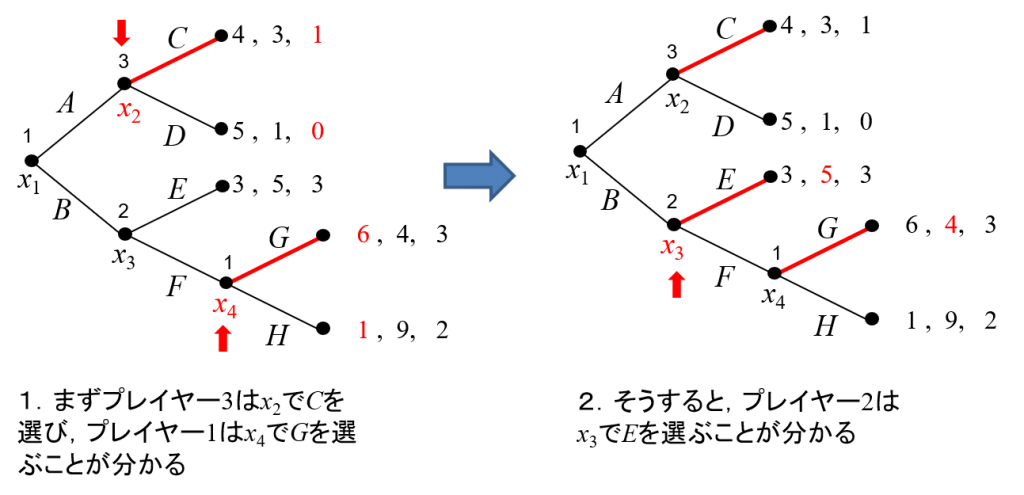
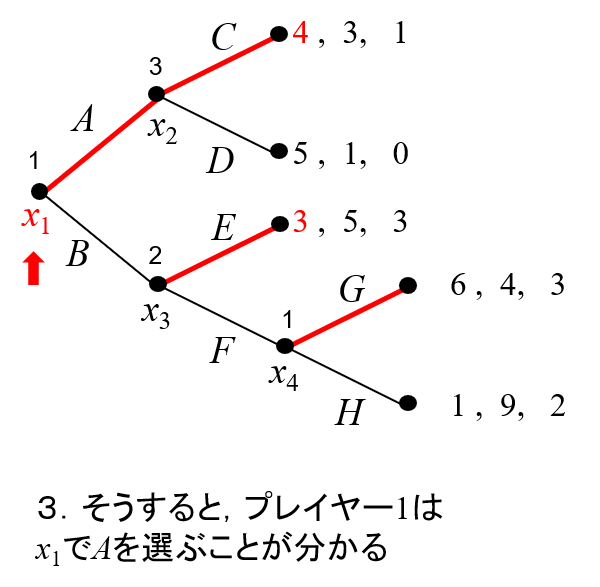
3。次に、\(x_1\)で行動するプレイヤー1の行動を決めます。\(x_1\)でプレイヤー1は、\(A\)を選ぶと(プレイヤー3が\(C\)を選ぶので) 利得が4、\(B\)を選ぶと(プレイヤー2が\(E\)を選ぶので)利得が3となるので\(E\)を選ぶ、ということになります。
解と結果(均衡経路)を区別する
以上、バックワードインダクションによる完全情報ゲームの解の求め方について解説しました。このときバックワードインダクションで得られるゲームの解と、それによって予測されるゲームの結果は何であるか、について区別しなければなりません。ここで
ゲームの解とは、すべての点で各プレイヤーが何を選ぶかを、すべて明らかにしていること
ゲームの結果とは、ゲームの解によって、最初(初期点)のプレイヤーから順番にどのような行動が選ばれゲームが進行して、どの点でゲームが終わるかを示したもの
です。
例えば最初の例1を見てみましょう(図6)。
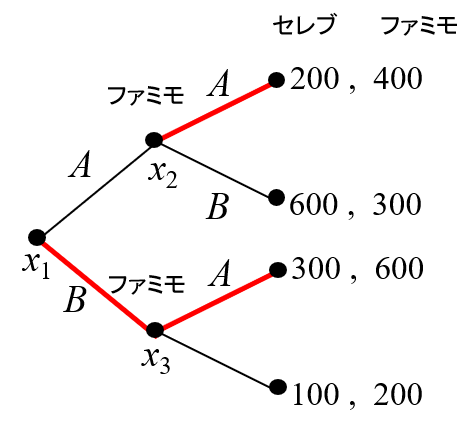
このときゲームの解は「 \(x_1\)でセレブがBを選び、\(x_2\)と\(x_3\)でファミモはAを選ぶ」となります。このようにゲームの解はすべての点でプレイヤーが何を選ぶかを定めたものです。
これに対し、\(x_1\)でセレブがBを選べば、次に\(x_3\)でファミモがAを選んでゲームは終わり、実際には\(x_2\) は実現しません。ゲームの解によって、実際に起きる結果は解の一部です。
「すべての点(正しくは意思決定点)で何が選ばれるか」が決まると、「最初のプレイヤー(初期点)から、順番にどのプレイヤーがどの行動を選んでゲームが進行して、最後のプレイヤーの行動が決まって利得が決まるところ(終点)」まで一本の経路(path)ができます。この経路は均衡経路(equilibrium path)と呼ばれます。この均衡経路はゲームの結果であると考えられます。 この例の場合、均衡経路(=ゲームの結果)は「 \(x_1\)でセレブがBを選び、\(x_3\)で、ファミモはAを選ぶ」となります。
「すべての意思決定点で何が選ばれるか」は「戦略の組(strategy profile)」に対応するものです。またこれは1つの経路を実現すると考えても良いし、1つの終点が決まると考えても良いです。なお途中で確率による選択(混合戦略)があると、経路は1つではなく、複数の経路が確率的に決定されると考えられます。
ゲームの解において、均衡経路ではない意思決定点は均衡外経路(off-equilibrium path)と呼ばれます。 例1では\(x_2\)は均衡外経路です。このことよりゲームの解が異なってもゲームの結果が同じになることがあることに注意しましょう。
例2で、ゲームの解とゲームの結果が何であるかを練習してみましょう。
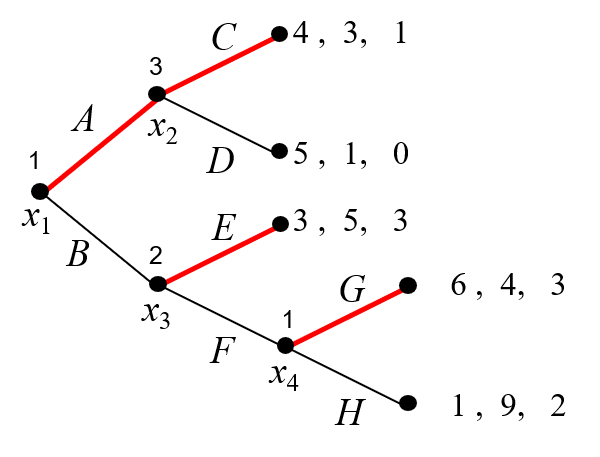
図7:ゲームの解と結果を区別する(例2)
この例2の場合は
- ゲームの解は、プレイヤー1が\(x_1\)で\(A\)を\(x_4\)で\(G\)を選び、プレイヤー2が\(x_3\)で\(E\)を選び、プレイヤー3が\(x_2\)で\(C\)を選ぶ。
- ゲームの結果は、プレイヤー1が\(x_1\)で\(A\)を選び、プレイヤー3が\(x_2\)で\(C\)を選ぶ。
となります。いかがでしょうか。
バックワードインダクションはゲーム理論だけではない
<後から解く>バックワードインダクションは、時間経過を伴う最適化問題である動的最適化(マクロ経済学、ファイナンス理論)、ネットワーク最適化問題にも用いられる一般的手法です。この概念を方程式に直すといわゆるベルマン方程式となります。
以下も参考にしてください。
