ゲーム理論は非協力ゲーム(non-cooperative game) と協力ゲーム(cooperative game) の2つの理論に分けられます。
ゲーム理論は、経済学の中で大きく発展したのですが、その経済学の中で扱われているのは、ほとんど非協力ゲームです。このため「ゲーム理論」と言う言葉は、非協力ゲームのことを指すことも多いです。実際に、ゲーム理論の代表的なテキストTadelis(2012)、Fudenberug and Tirole(1991) などでも協力ゲームは扱われていません。これに対し、近年ゲーム理論の研究が盛んな計算機科学の分野では、協力ゲームもそれなりに扱われ、研究されているように見えます。
非協力ゲームと協力ゲームの違い
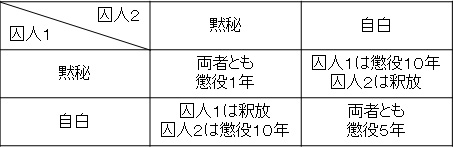
非協力ゲームでは、プレイヤーが利得が大きくなるように行動を選びます 。そして、各プレイヤーが行動を選んだ組み合わせに対し、プレイヤーの利得が与えられています。その中で、プレイヤーがどのように行動するかを明らかにすることが非協力ゲームの目的であると言えます。例えば非協力ゲームの代表的な例である囚人のジレンマ は:
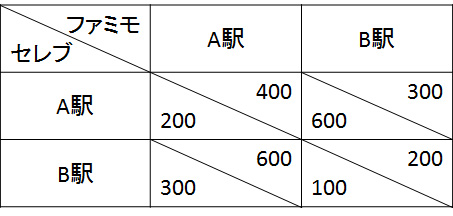
プレイヤーはA君、B君の2人 各プレイヤーは「協力する」か「協力しない」かの2つの行動から1つを選ぶ 各プレイヤーは次の順番に結果を好む自分が協力せず、相手が協力すれば 4点 自分も相手も協力すると 3点 自分も相手も協力しないと 0点 自分は協力して、相手が協力しないと 1点 のような感じです。利得行列 と呼ばれる表で、これを表すと以下のようになります。
囚人のジレンマの例 というモデルです。ここではプレイヤーの行動と、その行動の帰結に対して、自分が何を好むかが与えられています。このような設定で、各プレイヤーがどのような行動を選ぶのかを明らかにすることが非協力ゲームであると言えます。
これに対し協力ゲームは、プレイヤーの提携(集合、結託、グループなどと呼ばれる)に対する利益が与えられています。 例えば、
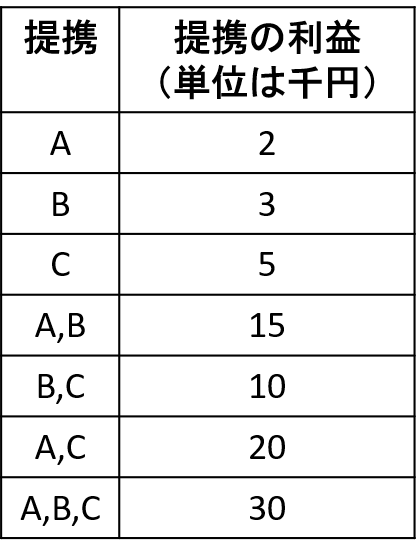
プレイヤーはA君、B君、C君の3人。大道芸をして稼ごうとしている。 A君、B君、C君は1人ずつだと1日の利益は、それぞれ2千円、3千円、5千円 A君とB君が一緒に組むと(これが「提携」)利益は1万5千円になる、B君とC君だと1万円、A君とC君だと2万円。 A君、B君、C君が3人で組むと、利益は3万円 と言ったモデルです。上記の設定は利得行列の代わりに、以下のような表で書くことができます。
協力ゲームの特性関数 上記の表は特性関数と呼ばれることから(本当は表ではなく、関数で書く)、協力ゲームは特性関数形ゲーム とも呼ばれます。
非協力ゲームと違い、プレイヤーには選ぶ「行動」がなく、 提携に対する利益だけが与えられています。このような設定で、全体の利益を個人にどう配分するべきか(配分されるのか) 、を明らかにすることが協力ゲームであると言えます。 上記であれば3人で協力して2万円の利益が得られたときに、その利益はA,B,Cにどのように分配されるのか、を明らかにすることが協力ゲームの目的であると言えます。
※「どのような提携が最終的に組まれるのか(全体提携が組まれるのか)」「そのとき利益はどのように分配されるのか」 を問題にすることもある。
なぜこのような違いが?
協力ゲームの特性関数は、もともとは非協力ゲームをベースにもとにして作られていました。例えば上の囚人のジレンマで特性関数を作ってみましょう。(本当は3人のゲームでやりたいのですが、3人の非協力ゲームや利得行列はややこしいので。)
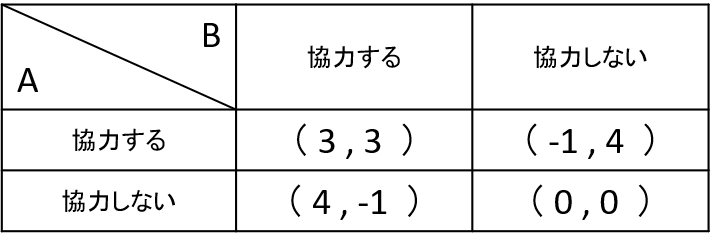
各プレイヤーは個人では、最低限の利得として0を獲得できます。一方、2人が協力すると合計の利益として6が獲得できます。したがって、囚人のジレンマの特性関数は
囚人のジレンマの特性関数 と書けます.
あれれ「書けます」とは言ったものの、本当にこれでいいのでしょうか?実は、ここに3つの問題点があることが分かります。
問題点1:全体の提携の利益を6にしているが、そもそも2人が協力できるなら囚人のジレンマなんて考える必要がない!個人の利益も0でいいの?
協力ゲームでは、提携の利益が本当に実現するのか、という問題が残ります。このため協力ゲームは提携を組んだときにその提携の利益が確実に得られる「拘束的合意」 と呼ばれる合意が存在すること が、前提になっているとも言われます。
このようにもともとは協力ゲームは、非協力ゲームの設定が与えられ、そこから各提携の利益が拘束的合意を前提に導かれるという形式が、出発点でした。しかしそれならば、その非協力ゲーム自身を分析して、それを個人の分配そのものと考えれば良いので、なんで非協力ゲームを考える必要があるの?、というわけです。
問題点2:提携の利益を考えるときに2人の利益を足している
これ足せるの?そして分配するときに、足した合計の利益を分けられるの?という問題があります。これについては、ゲーム理論における効用とは何か、というさらに深い問題に入り込まなければならないので、ここでは省略します。このような特性関数ゲームでは、各プレイヤーにとって価値尺度を共通して測れる(貨幣のような)別払い(side payment) と呼ばれる方法が存在することが前提とされます。
問題点3:たとえ拘束的合意と別払いがあったとしても、3人以上のゲームで、提携内と提携外でプレイヤーが何を選んだ場合を、提携の利益と考えるのか?
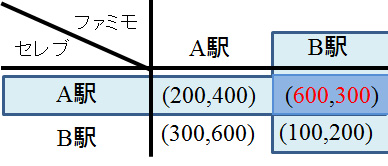
という問題があります。例えばA,B,Cの3人がいてAとBの提携の利益を求めたいとき、拘束的合意があって、AとBは2人の合計利益を最大にするように行動すると仮定しても、Cがどの行動を選ぶかで利益が異なってしまいます。
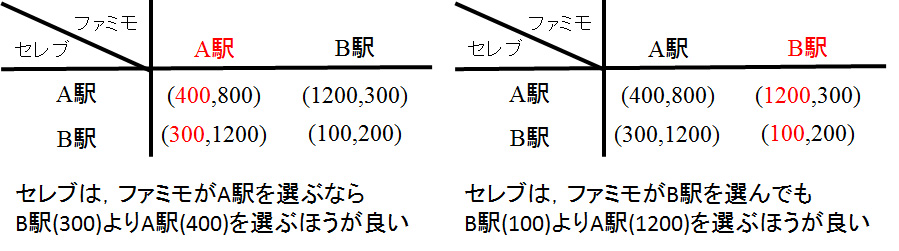
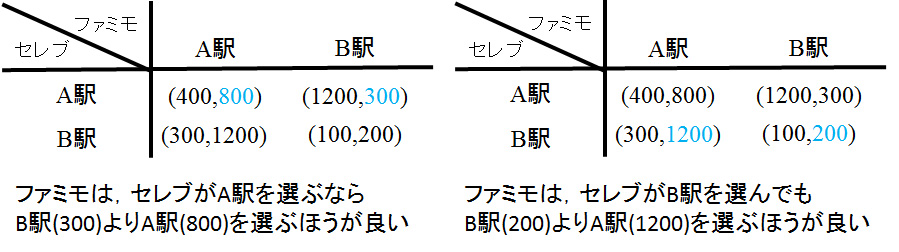
フォン・ノイマンとモルゲンシュテルンが考えた古典的なゲーム理論では、提携をまとめて1人のプレイヤーと考え、提携外のプレイヤーをまとめて1人のプレイヤーと考え、問題を2人ゲームに帰着させました。そして、そのゲームの解を提携の利益としています。しかし、その考えでいいのかという問題はありますし、フォン・ノイマン達が考えたゲームは零和ゲームだったので、2人ゲームの解のプレイヤーの利益は一意に決まるのですが、非零和ゲームではナッシュ均衡は複数あることもあり、利得も一意には決まりません。
協力ゲームは規範的な問題には効果的
目的によっては、協力ゲームのようなモデル化が便利な場合もあります。特に「どのような行動が選ばれて、どのような利益が得られるか」という「どうなるか(記述的理論)」ではなく、「提携ごとの利益から、どのように利益が各プレイヤーに配分されるべきか」という「どうあるべきか(規範的理論)」として活用できることが、協力ゲームの利点でもあります。
協力ゲームも非協力ゲームも、共にゲーム理論として発展してゆくべきだと私は考えています。