クールノー競争とベルトラン競争入門(3)：クールノー競争の価格・生産量と社会的総余剰

独占市場における価格と生産量の決定を理解したとして、ここでは２社のクールノー競争の価格と生産量の決定、および社会的総余剰の計算について説明します。

クールノー競争の価格と生産量の決定：モデル

ここでは同質財を販売している２社の生産量競争を考えます。一般にクールノー競争と呼ばれるのは、このモデルです（不完全競争市場の分類）。

企業AとBが同じ製品（同質財）を販売するとします。AとBの生産量をそれぞれ$x_A,x_B$とし、AとBは$x_A,x_B$を決定するとしましょう。
市場全体の生産量を$x=x_A+x_B$に対して、その価格$p$は$$p=a-bx$$で与えられるとします。
ここで製品を1単位の費用（限界費用）はAもBも$c$で同じであり、生産量にかかわらず一定とします。簡単にするため固定費は考えません。
AとBは利益を最大にすると考えます。AとBは、生産量$x_A、x_B$をいくらにするでしょうか。

問題の解法

問題は以下のようにして解くことができます。

企業Aの利益を$\pi_A$とおく。ここで（利益）＝（収入）－（費用）であり、収入は（価格）$\times$（生産量）、費用は（限界費用）$\times$（生産量）となります。したがって$$\pi_A=px_A-cx_A$$となります。
この$\pi_A$を最大にする$x_A$を考えます。そこで$p=a-bx$を代入し、さらに$x=x_A+x_B$に注意すると\[ \begin{align} \pi_A &= px_A-cx_A \\ &=(a-bx)x_A-cx_A \\&=
\{a-b(x_A+x_B)\}x_A-cx_A\\&=-bx_A^2-bx_Ax_B+(a-c)x_A　\tag{1} \end{align}\]となります。
この式(1)を最大にする$x_A$を求めるには、ざっくり言うと$x_A$で微分
（正確には偏微分）して0になるところを求めれば良い。(1)を$x_A$で微分すると、$-2bx_A-bx_B+(a-c)$となります。したがって\[-2bx_A-bx_B+(a-c)=0\]を解けば良く、これより\[x_A=-\frac{1}{2}x_B+\frac{a-c}{2b} \tag{2}\]となります。
式(2)は、企業Aの最適反応関数と呼ばれます。式(2)は$x_B$が与えられたときに企業Aの利益を最大にする企業Aの生産量を表しています。したがって、企業Bの生産量が決まれば、企業Aとの最適な生産量（答）が決まるのですが、企業Bの生産量がいくらになるか分かりません。そこで企業Bが利益を最大にする生産量を同様に求めてみます。
企業Bの利益を$\pi_B$とおきます。$$\pi_B=px_B-cx_B$$であり、企業Aの場合と同様に$p=a-bx$を代入して計算し、$$\pi_B=-bx_B^2-bx_Ax_B+(a-c)x_B$$を得ます。さらに$x_B$で微分して0になるところを求めると、\[x_B=-\frac{1}{2}x_A+\frac{a-c}{2b} \tag{3}\]となります。
この式(3)は、企業Bの最適反応関数と呼ばれます。企業Aと同様に$x_A$が与えられたときに、企業Bの利益を最大にする企業Bの生産量を表しています。
ここで、企業Aは企業Bの生産量が分からなければ、利益を最大にする生産量が分からず、企業Bは企業Aの生産量が分からなければ、利益を最大にする生産量が分かりません。ここでゲーム理論のナッシュ均衡の概念により解を求めるわけです。ナッシュ均衡は、お互いが最適反応戦略を選び合うような戦略の組み合わせで、ここでは式(2)と式(3)を同時に満たす$x_A$、$x_B$となります。
式(2)と式(3)を同時に満たす$x_A$、$x_B$は、これらを連立方程式で解くことによって求められます。式(3)の$x_B$を式(2)に代入して計算すると$x_A=-\frac{1}{4}x_A+\frac{a-c}{4b}$となり、これから$x_A=\frac{a-c}{3b}$を得ます。またこれを式(2)に代入して、$x_B=\frac{a-c}{3b}$を得ます。
このときの価格は\[p=a-bx=a-b(x_A+x_B)=\frac{a+2c}{3} \]となります。
このとき企業Aの利益は\[ \begin{align} \pi_A &= px_A-cx_A =(p-c)x_A\\ &=\left(\frac{a+2c}{3}-c\right)\left(\frac{a-c}{3b}\right)=\frac{(a-c)^2}{9b} \end{align}\] となります。同様に企業Bの利益も同じになります。

まとめますと、クールノー競争における企業Aと企業Bの生産量は$x_A=x_B=\frac{a-c}{3b}$となります。これをクールノー均衡と呼びます。クールノー均衡における価格は$p=\frac{a+2c}{3}$、各企業の利益は$\pi_A=\pi_B=\frac{(a-c)^2}{9b}$となります。

消費者余剰、社会的総余剰

独占市場における、消費者余剰、生産者余剰、社会的総余剰について示します。

市場全体の取引量が$x=x_A+x_B=\frac{2(a-c)}{3b}$であることに注意すると、上記で求めたクールノー競争の価格と生産量と企業の限界費用は、以下の図で示すことができます。

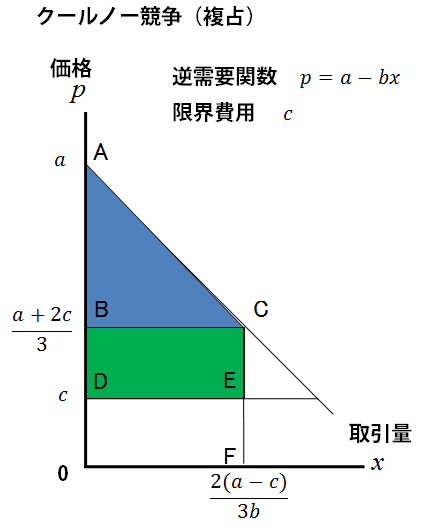
消費者余剰は、図の青色で示された部分の三角形です。

三角形の底辺の長さは$\frac{2(a-c)}{3b}$、高さは\[ a-\frac{a+2c}{3}=\frac{2(a-c)}{3} \]ですから、三角形の面積は\[ \frac{1}{2} \times\frac{2(a-c)}{3b} \times \frac{2(a-c)}{3}=\frac{2(a-c)^2}{9b} \]となります。

企業の利益は、図の緑色の部分の長方形の面積です。

長方形の高さ（価格－限界費用）は、$\frac{a+2c}{3}-c=\frac{a-c}{3}$、ヨコの長さは$\frac{2(a-c)}{3b}$ですので、長方形の面積は\[\frac{a-c}{3}\times\frac{2(a-c)}{3b}=\frac{2(a-c)^2}{9b}\]となります。先に求めた企業の利益を合計した値（$\pi_A+\pi_B$）と一致することがわかりますね。これを生産者余剰とも呼びます。

社会的総余剰は、消費者余剰と生産者余剰の総和です。したがって社会的総余剰は
\[\frac{2(a-c)^2}{9b}+\frac{2(a-c)^2}{9b}=\frac{4(a-c)^2}{9b}\]です。

オンライン講義

2020年東京都立大学「ゲーム理論1」オンライン講義（youtube）：コロナ対応