「高知競馬 快進撃の舞台裏」という特集のコメンテーターとして、NHK高知の制作番組「とさ金」に出演します。「競馬の経済学」を読んだディレクターから声をかけて頂きました。放送は今週の金曜6月21日19:30からの予定。高知県内だけの番組ですが、NHKプラスでは見られるようです。よろしければご覧ください!

追伸:
関連記事がこちらにあります。
追伸2:
好評につき、全国放送(7月13日(土)午前5:10-5:40)、国際放送(7月20日(土)午前5:15-5:45)でも放映されるようです。

Navigator to Game Theory
OR学会機関誌「オペレーションズ・リサーチ」2024年4月号の特集「エンジニアリングのためのゲーム理論」に「ゲーム理論のトリセツ」という記事を書きました。
また、Chat GPTを使いながら私が編集した小島武仁先生の講演録「社会の「ゲームのルール」を科学する―マーケットデザインの理論と実践―」も掲載されています。(1年間は学会員限定です)
中央分水嶺によって、太平洋と日本海に流れる水は分かれるのだけど、その分水嶺付近に川や湖があれば、その川や湖は両方に流れているはずだ。登山をしなくても、巡れるような川や湖を調べてみた。
「競馬の経済学」という本を監修しました。「〇〇の経済学」というと、経済学にはあまり関係がないお金の流れが書かれている本が多いんですが、この本も類に漏れず(^^;)、気軽に読める本です(経済学者の皆さんごめんなさい)。
2022年には3兆円を超えたJRAの売上は、どのように使われるのか。競争馬は一頭いくらくらいなのか?一番賞金を稼いだ馬は?調教師の年収はいくらくらい?など、楽しく読めて、飲み会で使えそうなネタがいっぱいです!

「ゲーム理論と競馬とマーケット」など、私のコラムも3本ほど載っています。これを機会に本HPの賭けとゲームの科学の記事も増やしていきたいです。どうぞよろしくお願いします。
背景
python+seleniumでchromeのバージョンアップに自動的に対応するために、webdriver managerを使っていたが、chromedriverのダウンロード環境が変わり、 webdriver manager がうまく動作しなくなった。したがって手動で chromedriver を更新しなければならなくなった。
しかし、seleniumの新しいバージョンにはselenium managerというのがデフォルトでついているようで、これを使うと webdriver_manager を使わなくても済む。これを使って上手くいくようになった。
(1)seleniumのアップグレード
pip install --upgrade selenium
バージョンが4.10.0以上になってくれればOK
(2)念のためwebdriver-managerをアンインストール
pip uninstall webdriver-manager
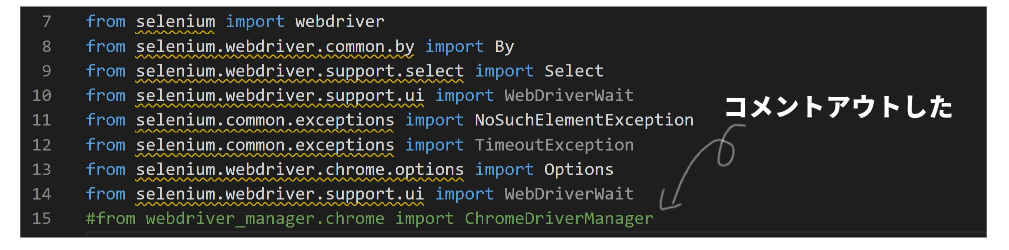
(3)コードからwebdriver_managerモジュールのimportを削除
from webdriver_manager.chrome import ChromeDriverManager
を削除
(4)ChromeDriverManagerを使っていた部分を変更
driver = webdriver.Chrome(ChromeDriverManager().install())を
driver = webdriver.Chrome()に変更。
これで動くようになったようだ、とりあえず。
裳華房より2021年に出版した拙著「一歩ずつ学ぶゲーム理論」は初めて学ぶ者も数式でゲーム理論を理解できることを目指した教科書です.
※本記事に対してメールを頂き、それを受けて少し書き直しました。ありがとうございました。(2024/03/16)
※修正した記事が間違ってましたので、直しました。ご指摘頂いた方、ありがとうございました(2024.03.22)
まずモンティ・ホール問題について説明しておきます。
司会者(モンティ・ホールさん)と回答者がいて、回答者の前にはA、B、Cの3つのドアがあります。1つのドアは当たりで豪華な商品があり、回答者はそのドアを当てます。2つのドアはハズレです。回答者が「当たり」のドアを当てる、というものです。
まず、回答者がが当たりと思うドアを1つ選びます。ここではAを選んだとしましょう。司会者は、当たりのドアを知っていて、回答者が選ばなかったドアのうち、1つのドアがハズレであることを示します。ここではBのドアがハズレだと示されたとしましょう。
ここで司会者が回答者に言います。「あなたには、もう一度ドアを選び直すチャンスがあります。そのままにしますか?それとも変えますか?(stick or switch?)」
今回の場合、Aのまま留まるか?Cに変えるか?ということになります。
さて、回答者はドアを変更すべきでしょうか?それとも留まるべき?
この問題、AとCの2枚のドアのうち1つが当たりなので、変えても留まっても当たる確率は半々(1/2)のように思えます。しかしこの問題の答は「変えたほうが良い」です。留まる(Aのまま)だと当たる確率は1/3、変えると(Cに変更)当たる確率は2/3になります。
なぜ、そうなるかについては、ベイズの定理を使って、数々のネットの情報や本で説明されています。拙著「ゼミナールゲーム理論入門」でも「一歩ずつ学ぶ ゲーム理論」でも、もちろん解説されています。
「お、じゃあネットで検索してみようか!」と思ったあなた!ちょっと待ってください。この問題に対して「直感的に説明すると...」とした説明には、間違っていることが結構あります。本稿の意図は「直感的な説明は間違っていることが多いので、ベイズの定理で理解しましょう」ということなんです。
特に「確率は変わらない」的な説明は、間違いです。例えば「最初に選んだドアが当たる確率は1/3、それ以外が当たる確率は2/3だから、ハズレのドアを開けた後も、最初に選んだドアの当たる確率は1/3で、それ以外が当たる確率は2/3」と言う説明は誤りです。正しい説明は「情報によって確率は変わる」です。
最初に各ドアの当たる確率が等しいと、この「確率は変わらない」という説明も(たまたま)正しいように見えるのですが、最初に当たりやすいドアと、当たりにくいドアがあると考えれば、この説明が正しくないことが分かります。
A,B,Cのドアがあり、どれか1つが当たりだとします。ただし、Aのドアは当たりやすく当たる確率は0.5、Bは当たりにくく当たる確率は0.2、Cは0.3であるとします。
回答者は最初に(当たりやすそうな)Aのドアを選んだとしましょう。
ここで司会者(解答を知っている)は、選んでないドアからハズレのドアを1つ開けます。Bのドアが当たりならCが開き、Cのドアが当たりならBが開きますね。さて、Aのドアが当たりの場合はBとCのどちらを開けても良いのですが、ここで司会者がBとCのドアを開ける確率は同じ1/2であるとします(ここを変えると答も変わります)。
さて、司会者がBのドアを開けて、ハズレであることを示したとします。回答者はドアを変えたほうが良いんでしょうか?
「最初にAのドアが当たる確率は0.5、それ以外は当たる確率は0.5、この確率は変わらない」という説明だとフィフティ・フィフティで、変えても変えなくとも確率は1/2のような気がします。
しかし、この場合はAのドアのままだと当たる確率は5/11、Cに変えると当たる確率は6/11です。この場合は、やはりドアを変えたほうが良いです。
ちなみに司会者がCのドアを開けてハズレであることを示すと、 Aのドアのままだと当たる確率は5/9、Bに変えると当たる確率は4/9です。この場合は、ドアを変えない方が良いのです。つまり、この場合は「司会者がBのドアを開けたときはCに変えたほうが良く、Cのドアを開けたときはAのドアのままが良い」です。
モンティ・ホール問題の本質は、ドアを開けたことが情報になっていて、開ける前の事前確率と開けた後の事後確率が変化している、ということにあります。なので「元の確率と変わらないから」 的な説明は間違っていることが多いのです。
A,B,Cのドアが当たる確率が、それぞれ0.54、0.13、0.33として同じ状況だとしましょう。司会者がドアを開ける前は「Aのドアが当たる確率は0.54、それ以外は当たる確率は0.46」です。司会者がBのドアを開けたとき、回答者はドアを変えたほうが良いのでしょうか?確率は変わらない」のならば「Aのドアが当たる確率は0.54」なので、変えないほうが良いですね。
しかしこの場合も「Aのドアのままだと当たる確率は0.45、Cに変えると当たる確率は0.55」になります。司会者がドアを開ける前は、Aを選んだ方が、それ以外のドアが当たる確率より高いにも関わらずです!
計算方法は、ベイズの定理を勉強してください。このように、この問題は「直感的な」理解はなかなか難しいのです。ネットの説明でも「情報によって確率は変わる」という回答を読むと良いでしょう。
認知科学や認知心理学では、なぜ人間はこの問題に対して正しい答が出せないのか、どのような点が間違いを引き起こすのかについて研究されています(いました)。興味にある方は、以下の本を参考にしてください。
市川 伸一 (著)、日本認知科学会 (編集)、確率の理解を探る―3囚人問題とその周辺 (認知科学モノグラフ 10) (1998)/5/1
ちなみに、若い頃、先輩の金融工学の大家KJ先生(川喜田二郎氏ではないよ)に「認知科学にこんな研究があります」と話したことがあります。そのときKJ先生曰く:
渡辺君。こんな研究は意味ないよ。
皆んながベイズの定理を正しく理解すれば良いだけだ!
…でした。直感的な理解ではなく、ベイズの定理で理解しましょう。
さて、この問題では「回答者が差したドアが当たりの場合は、司会者は残りの2つのドアを等しい確率で開ける」とされていました。これによって、回答者は、指さしたカーテンの中で、まだ開いていないドアに変えたほうが当たる確率が高い、となっています。
でも「司会者ができるだけ回答者に賞品を当てて欲しくない」と考えると、ドアをどのように開けると良いのでしょうか?これはゲーム理論になりますね。ゲーム理論のテキストの演習問題なんかでは、見かけるものです(私の記憶だと、たとえば「Scott Bierman and Luis Fernandez, “Game Theory with Economic Applications,” Addison Wesley, (1997)」などに載っていた気がします。)。
答はどうなるでしょうか?ベイズの定理とゲーム理論を勉強した皆さんなら簡単ですね!
2023年3月、日本オペレーションズリサーチ学会から普及賞を頂きました。嬉しいです。
評価された活動は、ORセミナーでの学会の貢献や理事や幹事などでの貢献でした。特に、OR学会が公益法人になるときへの貢献を評価していただいたようです。
これらは、一緒に普及に協力して頂いた皆さんや先生方のおかけでもあり、私だけ賞を頂いて恐縮しています。皆さんに感謝です。
同じ表彰式では、研究室の先輩である吉瀬章子先生(筑波大学)が、業績賞という栄誉ある賞を受賞しました。嬉しさ倍増です。
5月26日(金)に、私がオーガナイザーを務めさせて頂き、2023年第1回O Rセミナー 『エンジニアのためのゲーム理論-ビジネスへの応用とマーケットデザイン』をオンラインで開催致しました。
今回は(あの)東京大学マーケットデザインセンター長の小島武仁先生、慶応大学の松林伸夫先生と私でセミナーを行いました。
プログラム等の詳細はここにあります。
当日は50名余りの方にご参加いただきました。ありがとうございました。
政策研究大学院大学(GRIPS)の「ゲーム理論」春学期後期の講義情報と講義資料です。
フットボール批評という雑誌に、私のインタビュー記事が掲載されました。サッカーのPK戦をゲーム理論から見ると言うものです。

私の本などで紹介しているPK戦の混合戦略の話(例えばこちら)と、Ignacio palacious-Huerta (2003)のヨーロッパリーグでの実証研究 “Professionals Play Minmax”などを紹介しました。
フットボール批評という雑誌は、その前身のサッカー批評という雑誌から数えると20年近く続いている雑誌だそうですが、今号をもって休刊となるそうです。複雑な気持ちです。