戦略10以下の2人戦略形ゲームのナッシュ均衡を（混合戦略まで含めて）すべて計算するプログラムなど、趣味で作ったweb上の計算アプリケーションを提供しています。
- ナッシュ均衡計算プログラム
- 2人戦略形ゲームのナッシュ均衡を全列挙する計算アプリです（戦略は10以下）。
- 逆行列計算
- ナッシュ均衡の計算プログラムを作るときに、練習として作ったものです。
部分ゲーム完全均衡（ざっくりとした説明）
部分ゲーム完全均衡について、ざっくりと説明します。
部分ゲーム完全均衡(Subgame Perfect Equilibrium, SPE)とは「ある点から後がゲーム（部分ゲーム）とみなせるときには、プレイヤーはそのゲームのナッシュ均衡を選んでいる」と考えるゲームの解です。
次のようなゲームを考えてみましょう。
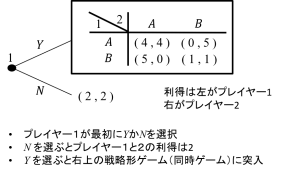
このゲームは最初にプレイヤー１がYかNかを選択。Nを選べば右上の戦略形ゲーム（同時ゲーム）に突入し、Nを選べばゲームは終了してプレイヤー1と2の利得が共に2となるゲームです。
このゲームの解はどうなると予想されるでしょう？プレイヤー１は最初の点で、Yを選んだときに、その結果がどうなるかを予想しなければなりません。右上の戦略形ゲームでは、ナッシュ均衡は(B,B)なので、プレイヤー1の利得は1になると予想されます。
このことからプレイヤー１は最初の点でYを選べば利得は1、Nを選べば利得は2になるのでNを選ぶと考えられます。部分ゲーム完全均衡は「プレイヤー１は最初の点でYを選び、次の戦略形ゲームでプレイヤー１と２は共にBを選ぶ」となります。
部分ゲーム完全均衡を正確に学ぶためには、(1)展開形ゲームはどのように書けて、それを戦略形ゲームに変換するにはどうするのか、(2)展開形ゲームにおいて、ある点から後をゲーム（部分ゲーム）とみなせるのはどういうときか、を学ぶ必要があります。それはまた今度にします。今はこちらの動画を参考にしてください。
部分ゲーム完全均衡はナッシュ均衡の１つ
部分ゲーム完全均衡はナッシュ均衡の１つ（精緻化されたもの）です。例を使って、（ボンヤリとですが）説明してみましょう。
次のゲームを考えます。
- 最初にプレイヤー１がUかDを選びます。Uを選べばゲームは終わり、プレイヤー１と２の利得は１と３になります。
- プレイヤー１がDを選ぶと、プレイヤー２がLかRを選びます。Lを選べばゲームプレイヤー１と２の利得は0と1、Rを選べばプレイヤー１と２の利得は共に2となります。
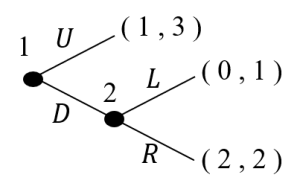
このゲームは、プレイヤー１がUかDを選び、プレイヤー２がLかRを選ぶ戦略形ゲーム（同時のゲーム）と考えることもできます。
ここで「交互にプレイする展開形ゲームを、同時にプレイする戦略形ゲームに変換できるのか？」という疑問があるかと思います。確かにそこが最大のポイントですね。確かにプレイヤー２は、プレイヤー１がDを選んだのを知ってから、LかRを選ぶわけです。しかし、プレイヤー２はゲームが始まる前に「もしプレイヤー１がDを選んだらどうするか」を決めておくことはできるはずです。またプレイヤー１は、「もしDを選んだらプレイヤー２はどうするか」を推測しなければ自分の選択を決めることができません。プレイヤー１の頭の中では、プレイヤー２がどうするかは、自分が選択をする前（ゲームが始まる前）に決まっていなければなりません。このように展開形ゲームでは「すべてのプレイが行われる前に、各プレイヤーはどの点で何が選ばれるかを決定しておく」として、戦略形ゲームとして考えることができるわけです。
この戦略形ゲームのナッシュ均衡は(U,L)と(D,R)の２つです。
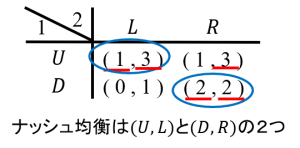
一方、このゲームの部分ゲーム完全均衡はどうなるでしょう。プレイヤー２が行動する点は部分ゲームと考えることができます。プレイヤー２はLを選べば利得1、Rを選べば利得2ですからRを選びます。このプレイヤー2の行動を推測すると、プレイヤー1はDを選びます。
均衡の精緻化
ナッシュ均衡がすべて、部分ゲーム完全均衡になるわけではありません。ここで、部分ゲーム完全均衡ではない(U,L)というナッシュ均衡が、どういうものかを考えてみましょう。図では以下のようになりますね。
このナッシュ均衡では、各プレイヤーが(U,L)が起こると予想しています。プレイヤー２は、プレイヤー１がUを選ぶと予想すれば、Lを選んでもRを選んでも利得は同じなので、Lを選んでも悪くはありません。そして、プレイヤー1は、プレイヤー2がLを選ぶと予想すれば、Uを選ぶことが最適です。したがって、この戦略の組は「すべてのプレイヤーにとって、相手がその戦略を選ぶならば、自分にとって最適な戦略を選んでいる」ようなナッシュ均衡になるのです。
確かにプレイヤー２は「プレイヤー１がUを選んだと予想したときは、Lを選んでもRを選んでも利得は同じ」です。しかし、このゲームは同時のゲームではありません。予想ではなく、実際にプレイヤー１がDを選んだ場合には、プレイヤー２は、もはやLを選ばずRを選ぶでしょう。
このように展開形ゲームを戦略形ゲームに変換すると、「プレイヤーが選択した行動の情報」を考慮せずに、プレイヤーの推測を考えることになってしまうように見えます（そう見えますが、本当にそうかどうかは、難しいところです）。
そのため、変換した戦略形ゲームのナッシュ均衡をそのまま解として考えると不完全で、展開形ゲームの構造を考慮して、ナッシュ均衡の中から適切でない解を除く必要があります。これを均衡の精緻化(equilibrium refinement)と呼びます。部分ゲーム完全均衡はナッシュ均衡の精緻化による解の１つです。
- 部分ゲーム完全均衡は「ある点から後がゲーム（部分ゲーム）とみなせるときには、プレイヤーはそのゲームのナッシュ均衡を選んでいる」と考えるゲームの解
- 部分ゲーム完全均衡はナッシュ均衡の１つ
- ナッシュ均衡から、適切でない解を取り除き、解の候補を絞り込むことを均衡の精緻化と言う
- 完全情報ゲームにおいては、部分ゲーム完全均衡はバックワードインダクションにいよる解になります。
東京都立大学 2020ゲーム理論１ オンライン講義（2020：コロナ対応）
調整ゲーム
調整ゲームはコーディネーションゲーム（coordination game）の翻訳で、協調ゲームと訳されることもあります。ざっくり言うと「他人と同じ行動を選ぶことが良い」ようなゲームです。結果となるナッシュ均衡は「全員が同じ行動を選ぶ」となるので（確率を用いる混合戦略を除く）、結果の候補が複数あることになります（複数均衡）。
女と男の戦い
ゲーム理論で最初に習う2人調整ゲームは、 以下のストーリーで表される女と男の戦い（battle of sexes）です（変な名前！でも昔は「両性の戦い」と訳されていました。これだとさらに意味不明です）。
アリスと文太は、禅寺かショッピングセンターに行く。2人は相手の行動を知らずに、どちらに行くかを選ぶ。アリスと文太は、お互いが好意を抱いているので同じ場所を選べば利得1を獲得し、さらにそれが自分が好きな場所ならば利得にもう1点が加わり2になる。違う場所を選んでしまうと（たとえ好きな場所に行ったとしても）利得は0である。
「女と男がいて、お互い同じ場所に行きたい。できれば自分の行きたいところがいい！」というそれだけのゲームです。男女が武闘しているわけではありません。この状況を利得行列にすると、以下のようになります。
この状況では、各プレイヤー（アリスと文太）はそれぞれ
(1)相手が禅を選ぶなら自分も禅を選ぶほうが良く
(2)相手がショッピングを選ぶなら、自分もショッピングを選んだほうが良い
となり、「相手と同じ行動を選ぶことが良い」となります。これが調整ゲームです。
調整ゲームの例
- どのSNSに参加するか、という問題。自分の友人が皆んなFaceBookを選んでいるならばFBを、インスタグラムを選んでいるならインスタを選ぶことが良い。このように商品に正の外部性（自分が購入する財から得る効用は、他の消費者がそれを多く選んでいるほど高くなる）があるときの消費者の選択は調整ゲームになります。
- 技術規格のデファクトスタンダード問題。かつてビデオデッキの開発において、各企業はVHS方式とベータ方式のどちらの規格を選ぶかという問題に直面しました。企業の選択は、多くの企業が選択するものと同じ規格を選択したほうが有利になります（wikipedia デファクトスタンダード）
- 同窓会の参加。皆んなが参加するならば、自分も参加したほうが良いけど、皆んなが参加しないなら、自分も参加しないほうが良い。
- 右側通行か左側通行か。細い道を車ですれ違うとき、右に避けるか左に避けるか。お互いに右か左か同じルールを選ばないと衝突してしまう。
調整ゲームのバリエーション
先ほどの「女と男の戦い」では、相手と同じ行動を選ぶことが良いわけですが、各プレイヤーは、どの結果が最良であるかが異なっています。アリスにとっては2人が禅を選ぶことが、文太には2人がショッピングを選ぶことが良いわけです。このような調整ゲームは非対称(asymmetric）であると言われます。これに対して「どの結果でも、2人が会えさえすれば同じ（1点）」のように、結果に差がなく、行動が一致さえすれば良いゲームは対称(symmetric)な調整ゲーム、純粋調整ゲーム(pure coordination game)、またはマッチングゲーム(matching game)と呼ばれます(Camerar 2003)。
2人とも買い物が好きで、禅寺で会えれば１点、ショッピング・センターで会えれば２点、のようなゲームも考えられます。このゲームでは、行動が一致しないより一致したほうが良いのですが、一致したときに皆にとって利得が高い場合と低い場合があります。このようなゲームには、定着した呼び名はありません。ここではTremblay and Horton(2012)に従いパレート調整ゲーム(Pareto coordination game)と呼んでおきます。
調整ゲームの解
調整ゲームでは、すべてのプレイヤーが同じ行動を選択することがゲームの解であるナッシュ均衡になります（他に確率を用いて選択を行う混合戦略のナッシュ均衡もあります）。例えば上述の女と男の戦いでは
(A)アリスも文太も禅寺に行く
(B)アリスも文太もショッピングに行く
という２つのナッシュ均衡があります（他に混合戦略のナッシュ均衡がある⇒最後の「注意点」を参照せよ）。実際にナッシュ均衡の求め方にしたがって利得に下線を引くと以下の図となり、両プレイヤーの利得に下線が引いてある戦略の組は、上記の(A)と(B)であることが分かります。
このように調整ゲームでは複数のナッシュ均衡が存在し、その中でどれを起こりうる結果である「ゲームの解」とするのか、という問題が起きます。この問題は均衡選択の問題と呼ばれ、ゲーム理論の大きな研究テーマです。
このときその中の１つのナッシュ均衡が起きるとすべてのプレイヤーが共通な認識で予測できるような理由があるならば、それは解となりえます。このような皆が共通して結果として予測できるような点はフォーカルポイントと呼ばれます（Schelling (1960)）。フォーカルポイントは、「社会慣習」や「これまで繰り返しプレイされてきて培われた経験」などによって形成されると言えます。
例えば上記の男と女の戦いでは、２人はいつも禅に行くことになっている（という慣習や経験があれば、２人は迷うことなく禅を選ぶでしょう。また、そのような経験がなくても「レディファースト」 （アリスに文太が譲る）という慣習があれば、やはり２人は禅を選ぶことになります。文太は、本当は２人でショッピングに行ったほうが良いのですが、アリスが禅に行くと予測するなら、ショッピングよりは禅が良い選択であり、アリスも文太が禅に行くと予測できるなら禅に行くことが良い選択です。つまりナッシュ均衡の定義である 「相手がそのナッシュ均衡の行動を選ぶなら、自分もそのナッシュ均衡の行動を選ぶことが一番良い」という条件を満たすことになります。
これに対して、上記のように２人が共通して予測できるフォーカルポイントがなければ、ナッシュ均衡は実現できるとは限りません。上記のようなゲームを実験室でやらせるとお互いが異なる行動を選び0点を食らってしまう結果も多く見られます。私も講義中にこの実験をやらせてみますが、うまくコーディネイトできるときもあれば、そうでない場合も多いです。うまくコーディネイトできない場合には、（当然ですが） 次の２つのパターンがあります：
・お互いに、自分が高い得点（2点）を選び合ってしまう。アリスが禅を、文太がショッピングを選び、お互いに0点を食らってしまう。
・お互いに、相手に高い得点を取らせようと譲ってしまう。アリスがショッピングを、文太が禅を選び、お互いに0点を食らってしまう。（私は「賢者の贈り物」パターンと呼んでいます。）
パレート調整ゲームでは、一般的にはプレイヤーにとって利得が高い<良い>ナッシュ均衡（パレート優位な均衡と呼ばれる） が望ましく、単純に考えるとそれが実現されると予想されますが、何らかの理由で両者にとって利得が低い＜悪い＞ナッシュ均衡が実現することも、十分あり得ます。先ほどの例２だと、２人ともショッピングに行くことで利得2が達成できるためこれが＜良い＞ナッシュ均衡ですが、例えば２人とも毎週毎週ずーっと禅寺に行っていることが定着していて、「相手は禅寺に行く」「相手は自分も禅寺に行くと予想するだろう」と考えれば(２人ともショッピングに行くほうが楽しいと分かっていても）禅寺に行くと考えられます。
調整ゲームにおいて、ナッシュ均衡が実現しない問題、ナッシュ均衡が実現してもパレート優位なナッシュ均衡が実現しない問題は、調整の失敗(coordination failure)と呼ばれます。
フォーカルポイントの例
単純なマッチングゲームでは、さまざまなフォーカルポイントがあると予想されますSchelling(1960)は、以下のようなゲームを（インフォーマルに）実験したようです。
- 表(head)か裏(tail)のどちらかを選べ。2人が同じものを選んだら賞金をあげよう。
- 好きな正の番号を選べ。2人が同じものを選んだら賞金をあげよう。
- ニューヨークのどこかで待ち合わせをする。どこで待ち合わせをするか選べ。
何を選んでも良いのですが、お互いに同じものを選ぶと良いので「調整ゲーム」であることが分かります。賞金に差もなく個人で選ぶと良いものに違いもないので、マッチングゲームですね。
Schelling(1960)によると最初のゲームでは42人中36人がheadを、2番めのゲームでは40%が「１」を選んだといいいます。3番めの質問では多数がGrand Central StationのInformation boothだとされています。
Mehta, Starmer and Sugden (1994)は、このような実験を精緻に行っています。この研究では被験者は２つのグループに分けられ、１つのグループC (Coordination)では「（ランダムに選ばれた）相手と同じものを選んだら賞金を与える」とされ、もう１つのグループP(Picking)では「何を選んでも賞金を与えるので、好きなものを選べ」としています。上記の最初の質問では、グループCでは87%、グループPでは76%がheadを選びそれほど差がないのに対して、2番めの質問では、グループCで選ばれたのは「１」が40%に選ばれて一番多く（「7」が2番めで14%）、グループPでは「７」が一番多く11%になっています。このことからある種の質問に対して、「自分が好きなもの」を選ぶのではなく「相手と同じものを選ぶためには何が良いか」を考えてそれを選ぶというフォーカルポイントが存在するということが分かります。
SchellingやMehta達は言及していないのですが、実験結果のデータを見て私が感じたのは「皆が同じものを選ぶと賞金をあげる」と言っているのに、自分が好きな数や場所を選ぶ被験者は、少数ながら必ずいるんだな…ということです。ルールが理解できていないのか、それとも何か意図があるのか.「フォーカルポイントに従う」という行動は、「大勢」や「傾向」ではありますが、それに逆らう（理解できない？従わない？）個の存在も無視できず、それはやはり「少数」や「個性」や「多様性」と言う社会科学の重要なテーマに繋がるのだな、と思いました。
注意点
- ここでは２人ゲームと多人数のゲームを曖昧に扱ってきましたが、厳密には分けて考えることが必要です。
- ここでは確率を使わない行動の選択（純粋戦略）のみを考えましたが、調整ゲームには各プレイヤーが確率を使って行動を選択する混合戦略を用いたナッシュ均衡もあります。例えば女と男の戦いの例だと「アリスは禅を2/3、ショッピングを1/3で選び、文太は禅を1/3、ショッピングを2/3で選ぶ」というナッシュ均衡があります。例１のマッチングゲームだと「アリスも文太も、禅とショッピングを1/2ずつ選ぶ」というナッシュ均衡があります。
- 相手と異なる行動を選ぶことが良いゲーム（チキンゲーム・混雑ゲーム）も広義の調整ゲームとみなされる場合があります。これはゲームの文脈を１回限りの２人のゲームと見做すか、多人数で長期間に渡って行われるゲームと考えるかで異なってきます。
- 調整ゲームにおいて「複数の均衡の中でどれが起きるか」という問題は、ゲーム理論における均衡選択という理論によって分析されており、リスク支配という概念によって起きる結果が選ばれます。
参考文献
- Camerar (2003), Behavioral Game Theory: Experiments in Strategic Interaction, Princeton Univercity Press.
- Mehta, Starmer, Sugden (1994), The nature of salience: An experimental investigation of pure coordination games, The American Economic Review, Vol.84, No.3, pp.658-673.
- Schelling(1960), The strategy of conflict, Harvard Univercity Press.
- Tremblay and Tremblay (2012), New Perspectives on Industrial Organization: With Contributions from Behavioral Economics and Game Theory, Springer.
以下も参考にしてください。
東京都立大学 2020ゲーム理論１ オンライン講義（2020：コロナ対応）
ナッシュ均衡の求め方：2人ゲームの利得行列の場合
ここではゲーム理論におけるナッシュ均衡を求める方法について。「プレイヤーが2人で混合戦略（確率を用いる戦略）を考えない場合」について説明します。ゲーム理論の基本中の基本と言えます。
ナッシュ均衡の求め方
ナッシュ均衡は「すべてのプレイヤーが最適反応戦略（利得が最も高くなる戦略）を選び合う戦略の組み合わせ」ですから、以下の方法で求めることができます。
- STEP1 プレイヤー１の立場で考える。
- 相手（プレイヤー２）のすべての戦略に対して、プレイヤー１がもっとも利得が高くなる戦略をチェックする（プレイヤー１の最適反応戦略）。ここでは利得に下線を引く。
- STEP2 プレイヤー１の立場でチェックが終わったら、プレイヤー２の立場で考える。
- 相手（プレイヤー１）のすべての戦略に対して、プレイヤー２がもっとも利得が高くなる戦略をチェックする（プレイヤー２の最適反応戦略）。ここでは利得に下線を引く。
- STEP3 すべてのチェックが終わったら、両プレイヤーの利得に下線が引かれているのがナッシュ均衡。（利得ではなく、戦略の組であることに注意！）
例題
以下の利得行列でナッシュ均衡を求めてみましょう。
今回は、ナッシュ均衡を求める手順を習得することが目的なので、ストーリーは特につけずに、単なる記号で利得行列を考えます。利得行列の読み方が不安、分からないって方は、こちらをご覧ください。
STEP1 まず、プレイヤー１の立場で考えます。相手（プレイヤー２）のすべての戦略に対して、プレイヤー１がもっとも利得が高くなる戦略（最適反応戦略）をチェックし、利得の下に下線を引いて行きます。
1.1 プレイヤー２がLという戦略を選んだ場合を考えます。プレイヤー１はTを選べば利得３、Bを選べば利得２です。したがってプレイヤー１はTを選びます（TがLに対する最適反応戦略）。そこでTを選んだ時の利得３に下線を引きます。
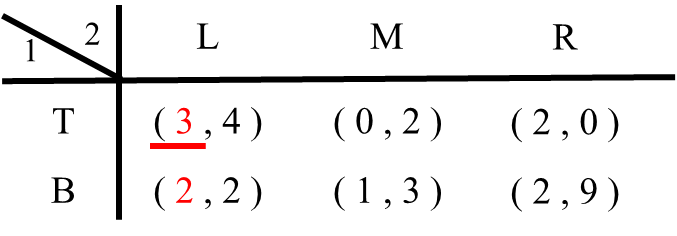
1.2 プレイヤー２がMという戦略を選んだら？プレイヤー１はTを選べば利得0、Bを選べば利得1です。したがってプレイヤー１はBを選びます（BがMに対する最適反応戦略）。そこでBの利得１に下線を引きます。
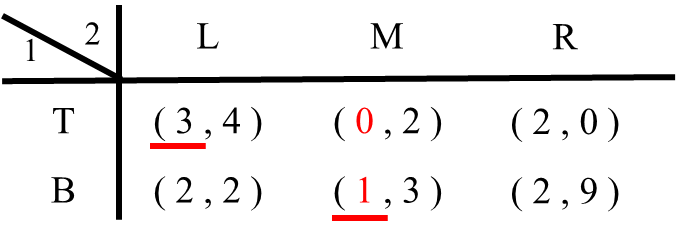
1.3 最後にプレイヤー２がRという戦略を選んだ場合を考えます。プレイヤー１はTを選んでも、Bを選んでも利得は２で同じです。この場合はTとBの利得２の両方に下線を引きます（ TもBもRに対する最適反応戦略）。
STEP2 プレイヤー１に対する検討が終わったので、次にプレイヤー２の立場で考えます。相手（プレイヤー１）のすべての戦略に対して、プレイヤー２の利得がもっとも高くなる戦略（最適反応戦略）をチェックし、利得に下線を引いて行きます。
2.1 プレイヤー１がTという戦略を選んだ場合を考えます。プレイヤー２はLを選べば利得４、Mを選べば利得２、Rを選べば利得０です。したがってプレイヤー２はLを選びます（LがTに対する最適反応戦略）。そこでLの利得４に下線を引きます。
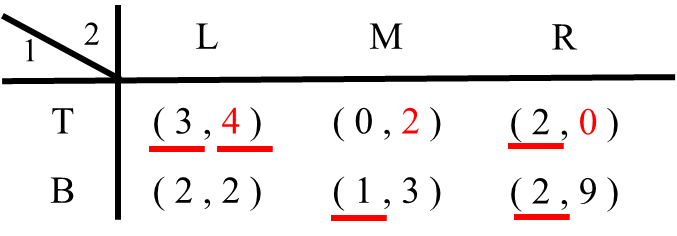
2.2 最後にプレイヤー１がBという戦略を選んだ場合を考えます。プレイヤー２はLを選べば利得２、Mを選べば利得３、Rを選べば利得９です。したがってプレイヤー２はRを選びます（RがBに対する最適反応戦略）。そこでRの利得９の下に線を引きます。
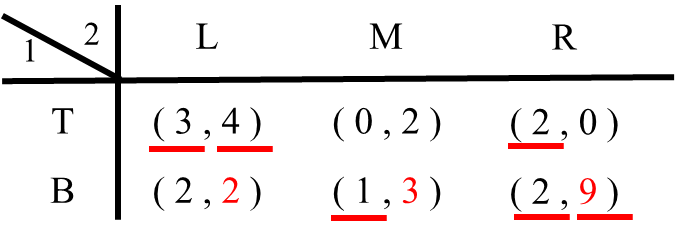
STEP３これでプレイヤー１とプレイヤー2のすべてのチェックが終わりました。プレイヤーの両方の利得に下線が引かれている戦略の組がナッシュ均衡です！「
ナッシュ均衡は「プレイヤー１はTを選び、プレイヤー２はLを選ぶ」「プレイヤー１はBを選び、プレイヤー２はRを選ぶ」の２つです。このようにナッシュ均衡は複数出てくる場合があります（これが悩みの種）。これを(T,L)と(B,R)のように、ベクトルのように書く場合もあります。
ナッシュ均衡は「戦略の組 (profile of strategies)」なので、戦略の組として答えます。「ナッシュ均衡は(3,4)と(2,9)です」などと答えては間違いです。それは利得の組ですから。「Tがナッシュ均衡」などと答えても間違いです。Tはプレイヤー１の戦略(a strategy of player 1）です。戦略の組み合わせではありません。
東京都立大学 2020ゲーム理論１ オンライン講義（2020：コロナ対応）
ナッシュ均衡を理解する演習
- 「ナッシュ均衡の求め方：2人ゲームの利得行列の場合」 も参考にして下さい。
利得行列や数式を用いずにナッシュ均衡を理解する
ゲーム理論の解はナッシュ均衡（こちらで説明）です。「ゲーム理論が少し分かった！」と思えるためには、ナッシュ均衡が理解できていなければなりません。しかし、よくあるゲーム理論の教え方では、ナッシュ均衡は利得行列を使って説明され、プレイヤーの利得が数式や数値や表で与えられて、それを機械的に計算しナッシュ均衡を求める人が多い気がしています。
利得行列からナッシュ均衡を求める方法はこちら（ナッシュ均衡の求め方：2人ゲームの利得行列の場合）。
しかし、それで正しくナッシュ均衡の概念が理解できたと考えられるでしょうか？（いやない、反語）。ここでは、数式や表を用いない例題でナッシュ均衡を理解していきましょう。
まずナッシュ均衡の定義をおさらいしましょう。ナッシュ均衡とは、
どのプレイヤーも、他のプレイヤーがそのナッシュ均衡の戦略を選んでいるならば、自分はそのナッシュ均衡の戦略を選ぶことが利得がもっとも高くなる。
です。つまり、
どのプレイヤーも、他のプレイヤーがそのナッシュ均衡の戦略を選んでいるならば、自分はそのナッシュ均衡の戦略以外を選ぶと、利得が同じか低くなる（高くなることはない）
ということです。この「同じか低くなる」と言うのは1つのポイントです。相手の戦略に対し、利得が最大になる戦略が１つならば「低くなる」で良いのですが、最大となる戦略が＜同点＞で2つ以上あるときは、「低くなるか同じ」 です。
なお「利得が高くなる」とは、プレイヤーにとって「良い」とか「好ましい」ということです。
2人ゲームの例
2人ゲームで練習してみましょう。なお以下では確率で戦略を選ぶ「混合戦略」は考えません。
練習１：アリスと文太は、禅寺かショッピングモールへ行く。アリスは禅が好きで、文太の行動に関わらず禅寺のほうがショッピングモールより良いと考えている。その中でどちらに行っても、文太に会えないよりは会える方が良いと考えている。一方、文太はどちらに行くかより、アリスに会えることが大切である。そして、アリスに会えたなら、ショッピングモールのほうが禅寺よりもいい。アリスに会えないときも同じである。以下から、ナッシュ均衡を選べ。複数あるときはすべて選び、ないときは「なし」と答えよ。
(A)2人とも禅寺へ行く
(B)アリスは禅寺へ、文太はショッピングモールへ行く
(C)アリスはショピングモールへ、文太は禅寺へ行く
(D)2人ともショッピングモールへ行く
正解は(A)。(A)では、どちらのプレイヤーも、自分だけが行動を変えると利得が小さくなるのでナッシュ均衡です。(B)では文太は禅寺へ行ったほうが利得が高くなりますし、(C)と(D)では、アリスは禅寺へ行ったほうが利得が高くなります。したがってナッシュ均衡ではありません。
なお(C)で「文太はショッピングモールに行ったほうが利得が高くなるのでナッシュ均衡ではない」としても良いです。「ナッシュ均衡ではない」ことを示すには、選択を変えると利得が高くなるプレイヤーが1人でもいることを示せば良いので、アリスと文太の両方について言わなくても、どちらか1人で良いわけです。なお上記の場合、アリスにとって禅寺に行くことは支配戦略です。支配戦略がある場合は、ナッシュ均衡では必ずその戦略が選ばれます。
次はどうでしょうか？
練習２：アリスと文太は、禅寺かショッピングモールへ行く。アリスも文太も、お互いのことが大好きで、どちらに行くかよりも、相手に会えるほうが大切である。ただし、アリスは、会えたときも会えないときも、禅寺のほうがショピングモールよりも良く、文太はショッピングモールのほうが禅寺よりも良い。以下から、ナッシュ均衡を選べ。複数あるときはすべて選び、ないときは「なし」と答えよ。
(A)2人とも禅寺へ行く
(B)アリスは禅寺へ、文太はショッピングモールへ行く
(C)アリスはショピングモールへ、文太は禅寺へ行く
(D)2人ともショッピングモールへ行く
正解は(A)か(D)。２人が会えている(A)と(D)では、どちらか一方だけが行動を変えると、そのプレイヤーの利得が小さくなるのでナッシュ均衡です。(B)と(C)で、どちらか一方だけが行動を変えると、そのプレイヤーの利得が高くなるのでナッシュ均衡ではありません
さてさて、次はどうでしょうか？
練習３：アリスと文太は、禅寺かショッピングモールへ行く。アリスは文太が大好きで、どこに行くかよりも文太に会えることが大切。そして、その中で会えても会えなくても、禅寺のほうがショピングモールよりも良いと考えている。文太は残念ながらアリスが嫌いで、どこに行くかよりもアリスに会わないほうが会えるより絶対良いと考えている。その中で、会えたときも会えないときも、禅寺よりショピングモールのほうが良い。以下から、ナッシュ均衡を選べ。複数あるときはすべて選び、ないときは「なし」と答えよ。
(A)2人とも禅寺へ行く
(B)アリスは禅寺へ、文太はショッピングモールへ行く
(C)アリスはショピングモールへ、文太は禅寺へ行く
(D)2人ともショッピングモールへ行く
この場合はナッシュ均衡は「なし」です。２人が会えている(A)と(D)では、文太が行動を変えると会えなくなって利得が高くなり、２人が会えていない(B)と(C)では、アリスが行動を変えると高くなるので、どれもナッシュ均衡ではありません。（なおこのような場合も確率で戦略を選ぶ混合戦略を用いると、ナッシュ均衡がありますが、その場合は利得を数値で表さなければ確率が計算できません）。
３人以上のゲームの例
ナッシュ均衡についての理解が深まってきたでしょうか？それでは３人以上の例を考えて、練習してみましょう。まず簡単な「多数決」を考えてみましょう。
練習４：（奇数人での多数決） 5人で「海」か「山」を選ぶ。 多い人数が選んだ方を選ぶと勝ち、少ない人数が選んだ言葉を選ぶと負け。当然、勝つほうが負けるより良いとします。以下から、ナッシュ均衡を選べ。複数あるときはすべて選び、ないときは「なし」を選べ。
(A) なし
(B) 全員が「海」を選ぶ
(C) 4人が「海」、1人が「山」を選ぶ
(D) 3人が「海」、2人が「山」を選ぶ
(E) 2人が「海」、3人が「山」を選ぶ
(F) 1人が「海」、4人が「山」を選ぶ
(G) 全員が「山」を選ぶ
正解は(B)と(G)です。 全員が同じ言葉を選ぶ(B)と(G)では、どの人も他者の選択はそのままで自分の選択を変えると利得が低くなるので、ナッシュ均衡です。それ以外では、少数派になっているプレイヤーは、他者の選択がそのままのときに自分の選択だけを変えると多数派となり、利得が高くなるので、ナッシュ均衡ではありません。
では、次はどうでしょう。ライアーゲームの最初に出てくる「少数決」です。少数派になったほうが勝ちです。
練習5：（奇数人の少数決） 5人で「海」か「山」を選ぶ。少ない人数が選んだ方を選ぶと勝ちで、 多い人数が選んだ方を選ぶと負け。以下から、ナッシュ均衡を選べ。複数あるときはすべて選び、ないときは「なし」を選べ。
(A) なし
(B) 全員が「海」を選ぶ
(C) 4人が「海」、1人が「山」を選ぶ
(D) 3人が「海」、2人が「山」を選ぶ
(E) 2人が「海」、3人が「山」を選ぶ
(F) 1人が「海」、4人が「山」を選ぶ
(G) 全員が「山」を選ぶ
正解は(D)と(E)です。それ以外では、多数派になっている人は、自分だけの選択を変えると少数派となり利得が高くなりますので、ナッシュ均衡ではありません。
これに対し(D)と(E)では、すべてのプレイヤーが自分だけ選択を変えても利得が高くならない（同じか低くなる）のでナッシュ均衡です。なぜかと言うと、少数派となったプレイヤーは自分の選択を変えると多数派になり利得が下がりますし、多数派のプレイヤーは自分だけが選択を変えても、やはり多数派になってしまい（多数派が変わってしまいます）利得は同じになります。
もうお腹いっぱいでしょうかね？それでは、最後の問題です。
練習6：（７人じゃんけん）7人でじゃんけんをします。もちろんすべてのプレイヤーは、勝ち、あいこ、負けの順に良い（利得が高い）とします。
(A) なし
(B) 7人ともにグーを出す
(C) 3人がグー、4人がパーを出す
(D) 1人がグー、2人がパー、4人がチョキを出す
(E) 2人がグー、2人がパー、3人がチョキを出す
(F) 3人がグー、2人がパー、2人がチョキを出す
答えは(E)と(F)です！(B)「7人ともにグーを出す」や (C)「3人がグー、4人がパーを出す」では、グーの人がパーに変えることで負けから勝ちに転じて利得が高くなります。また(D)「1人がグー、2人がパー、4人がチョキ」では、グーの人がチョキに手を変えると、アイコから勝ちに転じて利得が高くなります。したがってナッシュ均衡ではありません。しかし(E)と(F)の場合は、どの人も自分だけが手を変えても、あいこからあいこになるだけで利得は高くなりません。したがって、(E)と(F)はナッシュ均衡です。
ナッシュ均衡（ざっくりした説明）
ここではまずナッシュ均衡について、ざっくり説明します。
ナッシュ均衡とは
ゲーム理論におけるナッシュ均衡とは、ざっくりいうと
どのプレイヤーも、自分だけでは、それ以上利得が大きくできない状態
です。「状態」って言い方は不正確過ぎるか。もう少し正確に言うと、ナッシュ均衡とは
どのプレイヤーも、他のプレイヤーがそのナッシュ均衡の戦略を選んでいるもとでは、その戦略が一番利得が高くなる（他の戦略では利得が同じか低くなる）
ような戦略の組です。あんまり変わんないか。
ナッシュ均衡の例
例を挙げましょう（これは支配戦略を説明するときに用いた例の「客数」を変えたものです）。
２つのコンビニ、セレブ（セレブイレブン）とファミモ（ファミリーモール）が、まだコンビニがないA駅とB駅のどちらか一方に出店しようと考えている。コンビニを１日に利用する客はA駅が600人、B駅が750人である。セレブとファミモがもし違う駅を選べば、利用客を独占できる。しかし同じ駅に出店すると、ファミモが人気で、ファミモはセレブの2倍の客数を獲得できる。すなわち両方がA駅に出店すると、セレブ200人、ファミモ400人。B駅に出店すると、セレブ250人、ファミモ500人である。ここで客数を利得と考える。セレブとファミモはどちらの駅に出店するだろうか？
このゲームを利得行列で書くと下のようになります
例えば「セレブとファミモが共にA駅を選ぶこと」はナッシュ均衡ではありません。なぜならセレブは、ファミモがA駅を選んでいるなら、B駅に変えたほうが利得が高くなるからです。このように、他のプレイヤーの戦略が変わらないもとで、あるプレイヤーが選択を変えると利得が高くなるならば、その戦略の組はナッシュ均衡ではありません。
これに対し、例えば「セレブがA駅、ファミモがB駅を選ぶこと」はナッシュ均衡です。なぜならセレブもファミモも、相手がそれを選んでいる限り、自分の利得をもっとも高くしているからです。つまりナッシュ均衡では、
どのプレイヤーも（相手がその戦略を選んでいるならば）、それ以上利得を高くできない （他の戦略では利得が同じか低くなる）
と言うことになります。
ナッシュ均衡は2つ以上あるときもある
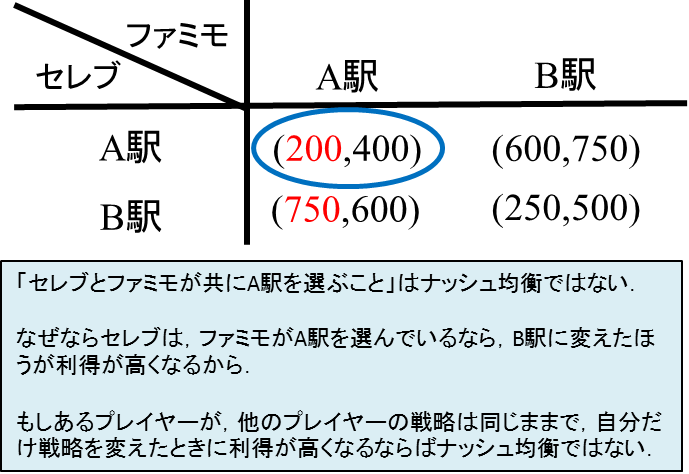
しかしこの例では「セレブがA駅、ファミモがB駅を選ぶこと」だけではなく、「セレブがB駅、ファミモがA駅を選ぶこと」 もナッシュ均衡になることが分かります。つまりナッシュ均衡は1つとは限らず、2つ以上ある場合もあります。このときどちらをゲーム理論の解とすべきかは難しい問題で、これは「均衡選択」と呼ばれる理論と「均衡精緻化」と呼ばれる理論で考えられています（2つの違いを説明するのはちょっと難しい）これはまた別の機会に。
ナッシュ均衡が複数あるゲームの代表例は、調整ゲームとチキンゲームです。調整ゲームの記事では、どういうときにナッシュ均衡が実現しやすいかについても述べています。
ナッシュ均衡がなぜ解なのか
ナッシュ均衡以外が結果として予測されたとします。このとき、もしすべてのプレイヤーがその予測を知ったならば、少なくとも1人はその予測から違う行動を取ることで利得を高くすることができるはずです。そのプレイヤーは、ナッシュ均衡と違う行動を取るでしょうから、もはやその予測は当たりません。このことから、ゲームの結果の予測をプレイヤーが知っても結果が成り立つためには、その予測はナッシュ均衡でなければならないはずです。（「じゃんけんの必勝法と行動ファイナンス・行動経済学」も参考にしてください）
注意点と補足
- すべてのプレイヤーが支配戦略を選んでいるときはナッシュ均衡になります。これはナッシュ均衡の特殊ケースと考えられます。したがって囚人のジレンマの結果もナッシュ均衡であると言えます。
- 上記の点から考えると、じゃんけんにはナッシュ均衡がありませんが、確率を用いる「混合戦略」を考えるとナッシュ均衡が存在します。このような混合戦略まで考えると、すべてのn人有限ゲームにナッシュ均衡が存在します。この素晴らしい定理を誰が証明したかは、よく考えれば分かるはずである。これによって、その人はノーベル経済学賞を受賞しています。私ではありません。
- ナッシュ均衡が分かったような気がしない？もう少し理解を深めたい？ではナッシュ均衡のおけいこ(1)で練習しましょう
- 2人ゲームの利得行列でのナッシュ均衡の求め方はこちら
- 混合戦略のナッシュ均衡の求め方
- クールノー均衡はこっち
東京都立大学 2020ゲーム理論１ オンライン講義（2020：コロナ対応）
非協力ゲームと協力ゲーム
ゲーム理論は非協力ゲーム(non-cooperative game)と協力ゲーム(cooperative game)の２つの理論に分けられます。
ゲーム理論は、経済学の中で大きく発展したのですが、その経済学の中で扱われているのは、ほとんど非協力ゲームです。このため「ゲーム理論」と言う言葉は、非協力ゲームのことを指すことも多いです。実際に、ゲーム理論の代表的なテキストTadelis(2012)、Fudenberug and Tirole(1991) などでも協力ゲームは扱われていません。これに対し、近年ゲーム理論の研究が盛んな計算機科学の分野では、協力ゲームもそれなりに扱われ、研究されているように見えます。
非協力ゲームと協力ゲームの違い
非協力ゲームでは、プレイヤーが利得が大きくなるように行動を選びます。そして、各プレイヤーが行動を選んだ組み合わせに対し、プレイヤーの利得が与えられています。その中で、プレイヤーがどのように行動するかを明らかにすることが非協力ゲームの目的であると言えます。例えば非協力ゲームの代表的な例である囚人のジレンマは：
- プレイヤーはA君、B君の2人
- 各プレイヤーは「協力する」か「協力しない」かの2つの行動から1つを選ぶ
- 各プレイヤーは次の順番に結果を好む
- 自分が協力せず、相手が協力すれば 4点
- 自分も相手も協力すると 3点
- 自分も相手も協力しないと ０点
- 自分は協力して、相手が協力しないと １点
のような感じです。利得行列と呼ばれる表で、これを表すと以下のようになります。
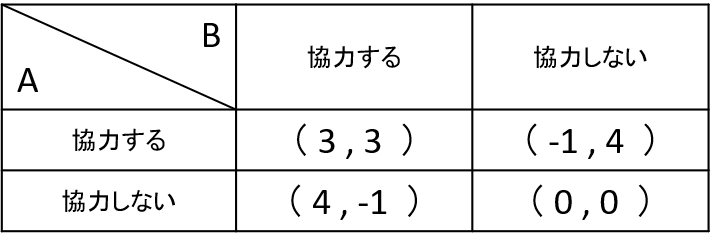
というモデルです。ここではプレイヤーの行動と、その行動の帰結に対して、自分が何を好むかが与えられています。このような設定で、各プレイヤーがどのような行動を選ぶのかを明らかにすることが非協力ゲームであると言えます。
これに対し協力ゲームは、プレイヤーの提携（集合、結託、グループなどと呼ばれる）に対する利益が与えられています。例えば、
- プレイヤーはA君、B君、C君の３人。大道芸をして稼ごうとしている。
- A君、B君、C君は１人ずつだと１日の利益は、それぞれ2千円、３千円、５千円
- A君とB君が一緒に組むと（これが「提携」）利益は１万５千円になる、B君とC君だと１万円、A君とC君だと２万円。
- A君、B君、C君が３人で組むと、利益は３万円
と言ったモデルです。上記の設定は利得行列の代わりに、以下のような表で書くことができます。
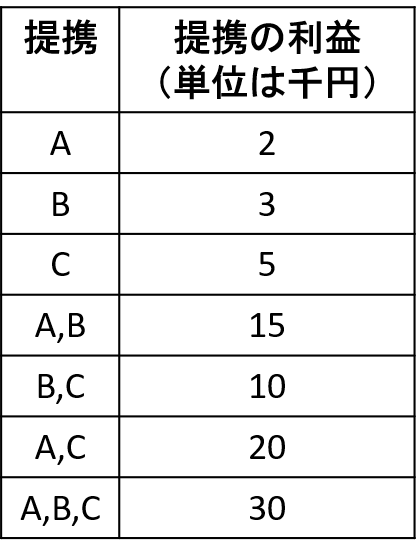
上記の表は特性関数と呼ばれることから（本当は表ではなく、関数で書く）、協力ゲームは特性関数形ゲームとも呼ばれます。
非協力ゲームと違い、プレイヤーには選ぶ「行動」がなく、提携に対する利益だけが与えられています。このような設定で、全体の利益を個人にどう配分するべきか（配分されるのか）、を明らかにすることが協力ゲームであると言えます。 上記であれば3人で協力して2万円の利益が得られたときに、その利益はA,B,Cにどのように分配されるのか、を明らかにすることが協力ゲームの目的であると言えます。
※「どのような提携が最終的に組まれるのか（全体提携が組まれるのか）」「そのとき利益はどのように分配されるのか」 を問題にすることもある。
なぜこのような違いが？
協力ゲームの特性関数は、もともとは非協力ゲームをベースにもとにして作られていました。例えば上の囚人のジレンマで特性関数を作ってみましょう。（本当は３人のゲームでやりたいのですが、３人の非協力ゲームや利得行列はややこしいので。）
各プレイヤーは個人では、最低限の利得として0を獲得できます。一方、2人が協力すると合計の利益として6が獲得できます。したがって、囚人のジレンマの特性関数は
と書けます.
あれれ「書けます」とは言ったものの、本当にこれでいいのでしょうか？実は、ここに3つの問題点があることが分かります。
問題点１：全体の提携の利益を６にしているが、そもそも２人が協力できるなら囚人のジレンマなんて考える必要がない！個人の利益も0でいいの？
協力ゲームでは、提携の利益が本当に実現するのか、という問題が残ります。このため協力ゲームは提携を組んだときにその提携の利益が確実に得られる「拘束的合意」と呼ばれる合意が存在することが、前提になっているとも言われます。
このようにもともとは協力ゲームは、非協力ゲームの設定が与えられ、そこから各提携の利益が拘束的合意を前提に導かれるという形式が、出発点でした。しかしそれならば、その非協力ゲーム自身を分析して、それを個人の分配そのものと考えれば良いので、なんで非協力ゲームを考える必要があるの？、というわけです。
問題点２：提携の利益を考えるときに2人の利益を足している
これ足せるの？そして分配するときに、足した合計の利益を分けられるの？という問題があります。これについては、ゲーム理論における効用とは何か、というさらに深い問題に入り込まなければならないので、ここでは省略します。このような特性関数ゲームでは、各プレイヤーにとって価値尺度を共通して測れる（貨幣のような）別払い(side payment)と呼ばれる方法が存在することが前提とされます。
問題点３：たとえ拘束的合意と別払いがあったとしても、３人以上のゲームで、提携内と提携外でプレイヤーが何を選んだ場合を、提携の利益と考えるのか？
という問題があります。例えばA,B,Cの３人がいてAとBの提携の利益を求めたいとき、拘束的合意があって、AとBは２人の合計利益を最大にするように行動すると仮定しても、Cがどの行動を選ぶかで利益が異なってしまいます。
フォン・ノイマンとモルゲンシュテルンが考えた古典的なゲーム理論では、提携をまとめて１人のプレイヤーと考え、提携外のプレイヤーをまとめて１人のプレイヤーと考え、問題を２人ゲームに帰着させました。そして、そのゲームの解を提携の利益としています。しかし、その考えでいいのかという問題はありますし、フォン・ノイマン達が考えたゲームは零和ゲームだったので、２人ゲームの解のプレイヤーの利益は一意に決まるのですが、非零和ゲームではナッシュ均衡は複数あることもあり、利得も一意には決まりません。
協力ゲームは規範的な問題には効果的
目的によっては、協力ゲームのようなモデル化が便利な場合もあります。特に「どのような行動が選ばれて、どのような利益が得られるか」という「どうなるか（記述的理論）」ではなく、「提携ごとの利益から、どのように利益が各プレイヤーに配分されるべきか」という「どうあるべきか（規範的理論）」として活用できることが、協力ゲームの利点でもあります。
協力ゲームも非協力ゲームも、共にゲーム理論として発展してゆくべきだと私は考えています。