収益等価定理とは、どんなオークションでも、売り手に与える収益は同じになるという驚くべき定理です。ここではセカンドプライスオークション(第2価格入札)、ファーストプライスオークション(第1価格入札)、競り(イングリッシュオークション)の3つのオークションについて考え、(1)セカンドプライスオークションでは参加者が自分の評価額をそのまま入札することが良いことや、(2)収益等価定理が成り立つ理由、などについて、直観的にざっくりと説明します。
セカンドプライスオークションと収益等価定理
ゲーム理論やオークション理論を習ってまず感激するのはセカンドプライスオークション(第2価格入札)というオークションの理論です。このオークションは1番高い入札をした人に、2番めに高い入札額で財を売るというヴィックリなオークションです(これを考えたVickreyにかけました.すみません)。
「おい、そんなことをしたら、売る人が損するんじゃね?」と思うひと。ゲーム理論やメカニズムデザインを勉強しましょう!そうではないんですよ。
普通のオークションは1番高い入札をした人に、その人の値段で売りますよね(ファーストプライスオークション=第1価格入札)。すると入札者は安く買うために入札額を下げようとします。ただし下げすぎると競争に負けて落札できないので、ここで迷うことになります。
ところがセカンドプライスオークションだと、落札者が財を購入する価格は自分の入札額ではない(自分の次に高い人の入札額)ので、安く入札しようが高く入札しようが、自分が買う値段には関係ないことになり、参加者の入札額は通常のファーストプライスオークションより高くなります。
参加者が安めに入札したファーストプライスオークションの1番高い入札額と、参加者が高めに入札したセカンドプライスオークション の2番めに高い入札額…どっちが売り手にとって良いか分からん、ということになります。これが同じになるっていうのが収益等価定理なんですね。
ここからは以下の例で考えてみましょう。いま真帆とはるかという2人の参加者がオークションに参加していて、売られている財(怪しい水晶玉)の評価をそれぞれ120万円、200万円としているとしましょう(図1)。

セカンドプライスオークションの戦略
さてオークションがセカンドプライスオークションであるとします。 ここでセカンドプライスオークションで、はるかは、自分の評価額を正直にそのまま入札することが最適な入札となることを説明します。
- 評価額の200万円より安い金額xを入札した場合。このように入札しても、もし落札できれば、200万円を入札したときと同じ金額で買うことになる。(相手の入札額が落札価格なので)。しかも相手がx万円以上を入札してきたときは、落札できないので評価額の200万円を入札したほうがいい。
- 評価額の200万円より安い金額yを入札した場合。このときは相手が200万円より高い入札をしても落札できる訳だが、それでは評価額より高い金額で買うことになってしまう(赤字)。相手が200万円より安い入札をしたら200万円でも落札できるので、評価額の200万円を入札したほうがいい。
- 図に示すと図2のようになる。
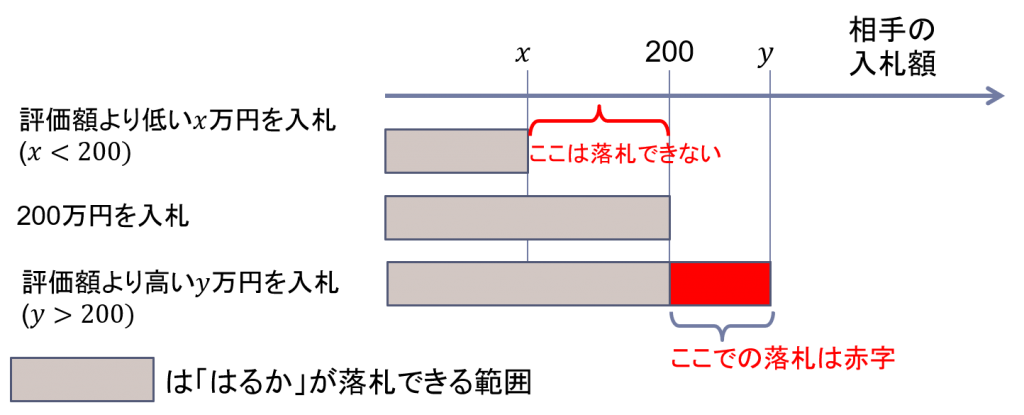
この話は相手の評価額や入札額が何であっても成り立つことに注意しましょう。セカンドプライスオークションでは、相手がどんな入札をしても自分の評価額を正直に入札することが良い、ということになります(これをゲーム理論では弱支配戦略と言う)。これがセカンドプライスオークションがヴィックリオークションと呼ばれる理由です(しつこくて、すみません)。 この性質はセカンドプライスオークションの耐戦略性と呼ばれ、メカニズムデザインにおいて重要な性質と考えられています。
このようにセカンドプライスオークション では参加者は自分の評価額を正直に入札します。その結果、売り手の収益は、2番目に高い参加者の評価額になります。図1の状況では、真帆は120万円、はるかは200万円を入札し、売り手ははるかに120万円で財を売ることになります。
ファーストプライスオークション
では通常の1番高い入札をした人に、その値段で売るファーストプライスオークションでは、どうなるのでしょうか。これはセカンドプライスオークションのように「相手がどんな入札をしても…」とは行きません。相手が高く入れれば高く、低く入れれば低く入れなければならないので、相手の評価額を推測する必要があります。そこで不完備情報ゲームの理論、確率論、微分方程式、と飛び道具を使わなければなりません。ここではそうも行かないので、単純化して相手の評価額が分かっているとして考えてみましょう。
図1の状況で、皆さんが「はるか」だったらいくらを入札するでしょうか?はるかは競争相手の真帆の評価額が120万円であることを知っているとしています。真帆が90万円くらい入札するなら、安く91万円くらいで買いたいところですが、はるかは真帆の評価額が分かっても入札額は分かりません。しかし真帆は120万円以上は絶対に入札してこないはずです。したがってはるかは120万円を超えるできるだけ安い価格を、可能であれば120万1円とかを入札すれば良いはずです。
つまりファーストプライスオークションでは、評価額が1番高い参加者は2番めに高い参加者の評価額の僅かに上を入札すれば良いわけです.「僅かに上」は無視できるとして、ファーストプライスオークションでは評価額が1番高い参加者が2番目に高い参加者の評価額を入札すると考えることができます。その結果、売り手の収益はやはり2番目に高い参加者の評価額になります。図1の状況では、真帆は120万円以下を、はるかはほぼ120万円を入札し、売り手はほぼ120万円で財を売ることになります。
競り
収益等価定理は競りにも適用できます。図1の状況で、30万円、40万円、50万円…と価格が競り上がっていく状況を考えましょう。このとき真帆やはるかはどうするでしょうか?

参加者は、自分の評価額を超えるまで、真帆は120万円まで、はるかは200万円まで競りに参加して、頑張るでしょう。しかし評価額になると、競りから降ります。その結果、真帆が120万円で落札することになります。

このように競りでは、評価額の2番めに高い参加者が降りた時点で、評価額の1番高い参加者が落札することになります。落札額は参加者の2番目に高い評価額になります。1番高い評価額には関係ないことに注意です、図の状況でたとえはるかが1億円まで出すつもりがあっても、真帆が120万円以上出す気がないなら、120万円で落札するわけです。その結果、競りでも売り手の収益はやはり2番目に高い参加者の評価額になります。
ちなみに競りで参加者は、相手の評価額を予想する必要はなく、自分の評価額まで競りに参加し、自分の評価額を超えれば競りから降りることが一番良いということが明らか(obvious)です。明らか均衡です。このことからセカンドプライスオークションと競りは、同等であるとも言えそうです。
収益等価定理
以上から、ファーストプライスオークション、セカンドプライスオークション、競りは、売り手に同じ収益を与え、それは参加者の2番めに高い評価額になるということが、ざっくりと分かりました。セカンドプライスオークションと競りでは相手の入札額に関係なく、このことが成り立つのですが、ファーストプライスオークションをはじめとする他の入札では、相手の評価額を確率に従って予測しなければなりません。結果としては、ある条件(後述)においては、どんなオークション(サードプライスオークションとか、一番安い入札額で売るとか、第1価格と第2価格の平均値で売るとか)でも、売り手の収益は2番目に高い参加者の評価額の期待値になる、というのが収益等価定理です。
定理の説明の補足、私的価値と相互依存価値
セカンドプライスオークションで評価額を正直に入札すれば良いという性質や、収益等価定理は入札者の評価額が他者の評価額に依存せず決まっている私的価値(private value)モデルについて成り立ちます。参加者が財に対して持つ価値が他者に依存する相互依存価値モデル(interdependent value)モデルでは、セカンドプライスオークションでも現在の評価額を正直に入札すれば良い、とは言えなくなります。
収益等価定理が成立するには(1)オークションで販売される財の価値に対して参加者が持つ価値は、他者とは独立に決まること (IPV:Independent Private Value)という条件以外にも、(2)その価値は事前には同一で独立の確率分布に従っていること、(3)参加者の行動は対称的(同じ価値であれば同じ入札額になるという感じ)であること、(4)参加者はリスク中立的であること、などが必要です。これらの条件が成立しない場合は、オークション形式により、売り手に与える期待収益は異なります。
定理を正しく理解するには、(1)ゲーム理論の不完備情報ゲームを修得し、(2)確率に対する知識を持ち、その中でも順序統計量という理論を理解し、なおかつ(3)微分方程式が解けなければならない、というもので意外と(かなり?)手強いです。なので、セカンドプライスオークション、競り、ファーストプライスオークションの3つのオークションについて、収益等価定理が成り立つ理由について、かなりいい加減ですが、直観的な説明をしました。
