Navigator to Game Theory
フットボール批評という雑誌に、私のインタビュー記事が掲載されました。サッカーのPK戦をゲーム理論から見ると言うものです。
私の本などで紹介しているPK戦の混合戦略の話（例えばこちら）と、Ignacio palacious-Huerta (2003)のヨーロッパリーグでの実証研究 “Professionals Play Minmax”などを紹介しました。
フットボール批評という雑誌は、その前身のサッカー批評という雑誌から数えると20年近く続いている雑誌だそうですが、今号をもって休刊となるそうです。複雑な気持ちです。
篠原さんというゲームデザイナーの方が発案した「よくばりじゃんけん（または、篠原じゃんけん）という面白いじゃんけんがあるそうです。
知らなきゃ損する？ ボードゲームに欠かせない「ゲーマーじゃんけん」と「よくばりじゃんけん」のルール
そのナッシュ均衡を一橋大学の宇井先生が求めています。以下に、宇井先生の原稿があります（篠原じゃんけんの説明も、その中にあります）
宇井先生の求め方は秀逸です。このじゃんけんは、グーを出すと、それによって脱落する人が出て人数が変わるため、普通は再帰的にしか求められないのですが、宇井先生は混合戦略均衡の性質と対称性をうまく利用して、きれいに解かれています。
多人数で勝者を決定するじゃんけんには「わたなべじゃんけん」がありますが、「生き残るかどうか！」というゲーム性と面白さは、さすがゲームデザイナー！ですね。
昨年(2021年）の10月に東京都立大学のオープンユニバーシティで講義した「高校生のためのゲーム理論入門」（高校生のための大学授業体験シリーズ）の動画が、東京都立大学のホームページ内でOCWとして公開されることになりました！
2021年度東京都立大学オープンユニバーシティ・高校生のための大学授業体験シリーズ 高校生のためのゲーム理論入門
他のゲーム理論講義動画とともにどうぞ
2021年度は筑波大附属高校の他に、八王子東高校でも「探究学習」のゲーム理論プロジェクトのお手伝いをしました。3月12日（2022年）には、その成果発表会があり、参加させて頂きました。
当日はゲーム理論だけではなく、物理化学、生物、哲学、心理学、スポーツ、ジェンダーなど、さまざまなプロジェクトのすべての成果が発表されていました。多くの会場で同時並行的に発表会が行われ、さながら学園祭のようでした。
生徒たちの間に実行委員があり、発表会が行われるようです。すごい！（委員長と副委員長の開会と閉会の挨拶も素晴らしかったです）。
ゲーム理論プロジェクト発表は、主に体育館のポスターセッションでした。発表数も多く、ゲーム理論プロジェクトだけでも、全部を聞けなくて残念でした。
以下は研究テーマの例です。
今回のゲーム理論プロジェクトは高校1年生の発表でした。ゲーム理論は高校1年生には少し難しいかなとも思たのですが、皆さん、私の「ビジュアルゲーム理論」を参考書にし、よく勉強して、素晴らしい成果を発表していました。⇒アマゾン
今回の探究学習のお手伝いを通じて、混合戦略などを、どのように高校生に教えればよいか、考えさせられました。高校生を主にターゲットにしながら、ゲーム理論を面白く教えるような教材を作っていきたいと思うようになりました。
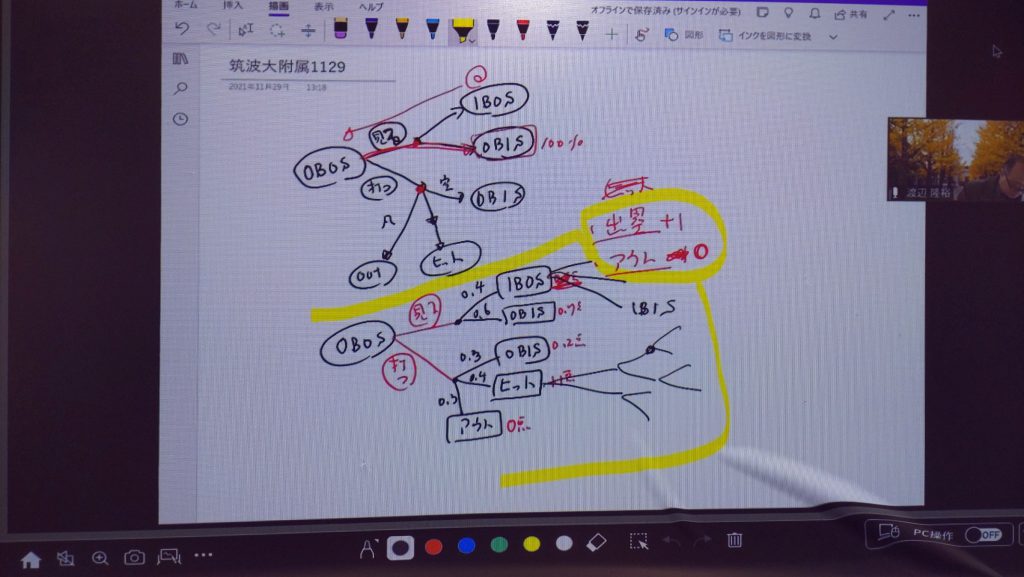
筑波大学附属高校で「総合的な探究の時間」のお手伝いをしてきました。高校１年生の「数学的モデリング」をテーマにしたグループで、ゲーム理論の講演をしたり、彼らの研究に助言を与えたりしました。
生徒たちは、ゲーム理論を中心に、自分の興味がある研究テーマに取り組みます。微分も確率もほとんど習っていない高校１年生とは思えないほどの高度な研究に取り組んでいました。テーマの例を挙げると
です。また、特に高校生にとってはゲーム理論によるスポーツの戦略に興味があるようで
などのテーマが多く見受けられました。
スポーツの戦略と混合戦略については、いくつかの研究はあるものの、それを詳しく解説したものはありません。改めて、そのような解説を書いてみようかと思いました。
多くの学生のテーマに向き合い、短い時間でアドバイスを与える担当の山田先生は、本当に凄いなと思いました。学生たちの探求は、まだまだ続くようです。
2022年のお正月！ナッシュ均衡を計算するプログラム（webアプリ）を作成しました。2人戦略形ゲームのナッシュ均衡を（混合戦略まで含め）すべて計算するプログラムです（ただし戦略は10以下）。日本には、ありそうでないんじゃないか、と思います。ぜひ、使ってみてください。
戦略10以下の2人戦略形ゲームのナッシュ均衡を（混合戦略まで含めて）すべて計算するプログラムなど、趣味で作ったweb上の計算アプリケーションを提供しています。
部分ゲーム完全均衡について、ざっくりと説明します。
部分ゲーム完全均衡(Subgame Perfect Equilibrium, SPE)とは「ある点から後がゲーム（部分ゲーム）とみなせるときには、プレイヤーはそのゲームのナッシュ均衡を選んでいる」と考えるゲームの解です。
次のようなゲームを考えてみましょう。
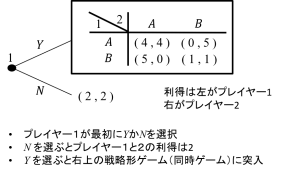
このゲームは最初にプレイヤー１がYかNかを選択。Nを選べば右上の戦略形ゲーム（同時ゲーム）に突入し、Nを選べばゲームは終了してプレイヤー1と2の利得が共に2となるゲームです。
このゲームの解はどうなると予想されるでしょう？プレイヤー１は最初の点で、Yを選んだときに、その結果がどうなるかを予想しなければなりません。右上の戦略形ゲームでは、ナッシュ均衡は(B,B)なので、プレイヤー1の利得は1になると予想されます。
このことからプレイヤー１は最初の点でYを選べば利得は1、Nを選べば利得は2になるのでNを選ぶと考えられます。部分ゲーム完全均衡は「プレイヤー１は最初の点でYを選び、次の戦略形ゲームでプレイヤー１と２は共にBを選ぶ」となります。
部分ゲーム完全均衡を正確に学ぶためには、(1)展開形ゲームはどのように書けて、それを戦略形ゲームに変換するにはどうするのか、(2)展開形ゲームにおいて、ある点から後をゲーム（部分ゲーム）とみなせるのはどういうときか、を学ぶ必要があります。それはまた今度にします。今はこちらの動画を参考にしてください。
部分ゲーム完全均衡はナッシュ均衡の１つ（精緻化されたもの）です。例を使って、（ボンヤリとですが）説明してみましょう。
次のゲームを考えます。
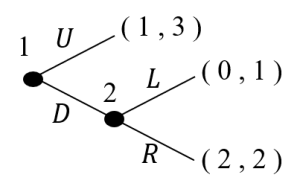
このゲームは、プレイヤー１がUかDを選び、プレイヤー２がLかRを選ぶ戦略形ゲーム（同時のゲーム）と考えることもできます。
ここで「交互にプレイする展開形ゲームを、同時にプレイする戦略形ゲームに変換できるのか？」という疑問があるかと思います。確かにそこが最大のポイントですね。確かにプレイヤー２は、プレイヤー１がDを選んだのを知ってから、LかRを選ぶわけです。しかし、プレイヤー２はゲームが始まる前に「もしプレイヤー１がDを選んだらどうするか」を決めておくことはできるはずです。またプレイヤー１は、「もしDを選んだらプレイヤー２はどうするか」を推測しなければ自分の選択を決めることができません。プレイヤー１の頭の中では、プレイヤー２がどうするかは、自分が選択をする前（ゲームが始まる前）に決まっていなければなりません。このように展開形ゲームでは「すべてのプレイが行われる前に、各プレイヤーはどの点で何が選ばれるかを決定しておく」として、戦略形ゲームとして考えることができるわけです。
この戦略形ゲームのナッシュ均衡は(U,L)と(D,R)の２つです。
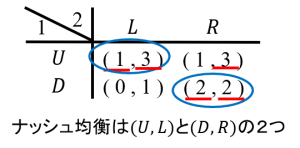
一方、このゲームの部分ゲーム完全均衡はどうなるでしょう。プレイヤー２が行動する点は部分ゲームと考えることができます。プレイヤー２はLを選べば利得1、Rを選べば利得2ですからRを選びます。このプレイヤー2の行動を推測すると、プレイヤー1はDを選びます。
ナッシュ均衡がすべて、部分ゲーム完全均衡になるわけではありません。ここで、部分ゲーム完全均衡ではない(U,L)というナッシュ均衡が、どういうものかを考えてみましょう。図では以下のようになりますね。
このナッシュ均衡では、各プレイヤーが(U,L)が起こると予想しています。プレイヤー２は、プレイヤー１がUを選ぶと予想すれば、Lを選んでもRを選んでも利得は同じなので、Lを選んでも悪くはありません。そして、プレイヤー1は、プレイヤー2がLを選ぶと予想すれば、Uを選ぶことが最適です。したがって、この戦略の組は「すべてのプレイヤーにとって、相手がその戦略を選ぶならば、自分にとって最適な戦略を選んでいる」ようなナッシュ均衡になるのです。
確かにプレイヤー２は「プレイヤー１がUを選んだと予想したときは、Lを選んでもRを選んでも利得は同じ」です。しかし、このゲームは同時のゲームではありません。予想ではなく、実際にプレイヤー１がDを選んだ場合には、プレイヤー２は、もはやLを選ばずRを選ぶでしょう。
このように展開形ゲームを戦略形ゲームに変換すると、「プレイヤーが選択した行動の情報」を考慮せずに、プレイヤーの推測を考えることになってしまうように見えます（そう見えますが、本当にそうかどうかは、難しいところです）。
そのため、変換した戦略形ゲームのナッシュ均衡をそのまま解として考えると不完全で、展開形ゲームの構造を考慮して、ナッシュ均衡の中から適切でない解を除く必要があります。これを均衡の精緻化(equilibrium refinement)と呼びます。部分ゲーム完全均衡はナッシュ均衡の精緻化による解の１つです。
グリコ・チョコレート・パイナップルじゃんけんについて。このゲームは勝ちと負けしかないゲームなのに、ネットなどでは3点や6点の利得を割り当て誤って計算されている例が多いです。実は拙著「ゼミナールゲーム理論入門」でも、初心者向けにと思って、そのような得点を仮定して解を求めて見せているのですが、それがそのまま本当の答えだと捉えられている傾向があり、これを正すまでは死ねないと思って書きましたよ。ぜひ、見てください！ ⇒ グリコ・チョコレート・パイナップルゲームのゲーム理論による解
グリコ（グリコじゃんけん）は「勝ち」と「負け」しかないのに、3点や6点の得点を割り当てて誤って計算されている答が多く、ゲーム理論として正しく解かれたものは（自分が知る限り）存在しない。ここでは 「グリコ・パイナップル・チョコレート」ゲームの正しい解について分析する。
このゲームは古くから知られていて、今でも子どもたちが遊んでいるのを見かける。多くの者の興味を引くようで、考察しているホームページや文献はいくつかあるが、どれも正しくない。…ということで、2019年度の渡辺ゼミの卒論で上野陽菜さんがこの問題に取り組んでくれたので、以下に発表。
本来は日本OR学会の2020年春季研究発表会で発表する予定であったが、コロナウィルス問題で学会が中止になったためここに公開。
結果の要旨を先にまとめると：
「グリコ・パイナップル・チョコレート」はスタート地点からじゃんけんをして、グー（以下G）で勝てば「グリコ」で３歩進み、チョキ（以下C）かパー（以下P）で勝てば「チヨコレイト」「パイナツプル」で６歩進んで、先にゴールしたほうが勝ち、というゲームである。古くから知られていて、私が子供の頃、50年くらい前には既に存在していたが、今でも子どもたちが遊んでいるのを見かける。この記事では、この「グリコ・チョコレート・パイナップル」ゲームの2人のときのゲーム理論における解を解析する。
もし、この2人ゲームの利得行列を図１の左側（進む歩数、進まれた歩数が利得）と考えるならば、ナッシュ均衡（零和ゲームなのでマキシミニ戦略と同じ）は「G,C,Pを2/5、2/5、1/5（2:2:1)で出す」ことが解になる。（求め方はいろいろなところに書いてある、例えばwikipedia） また右側と考えるならば「G,C,Pを1/4,1/2,1/4で出す」ことが解になる。
ちなみに右側は拙著「ゼミナールゲーム理論入門」に載っていて、求め方も（丁寧に）解説している。初心者にゲーム理論への興味を湧かせるために、このような例を用いたのだが、いつの間にかこの例が広まってしまった。中には「この解はおかしい」という人まで現れた。いやね、おかしいのは分かってて「このような利得だと考えると」と注意をしているのに…。失敗だった。いつか、これを正しておかなければ死ねないと、ずっと思っていた。本稿を仕上げることで、やっと死ねる。
図１のようなモデル化は間違っている。誤りの1つ目の点は、このゲームは元々「先にゴールしたほうが勝ち」というルールであり結果は「勝ち」「負け」しかなく、進んだ歩数が利得ではないからである。3とか6などの数値には正確な意味がなく、勝つか負けるかしかなく、勝ちは+1、負けは-1というゲームになるはずだ。
もう１つ上記のモデルが誤っている点、見落としている点は、このゲームは相手と自分が立っている位置によって、戦略が異なるということである。これを確認するには2人ともあと三歩以内でゴールできるという状態を想定すれば良い。このときは３歩でも６歩でもゴールできるので、G,C,Pは同じ効果を持つ（与える利得は同じ）。このときのナッシュ均衡は普通のじゃんけんと同じ「G,C,Pを1/3ずつ出す」となることは明らかだ。すなわち、このゲームにおける均衡戦略は「お互いが、あと何歩でゴールできるか」という状態に依存する。
ここではゲームを「先にゴールすれば勝ち、ゴールされれば負け」と考え、「勝てば利得が1、負ければ利得が-1」の2人零和ゲームと考える。そして2人のゴールまでの距離を状態変数としたゲーム（マルコフゲーム）と捉え、定式化して分析する。
このゲームを2人零和ゲームと考え、以下のようにモデル化する。
プレイヤー1が、あと\(n\)ステップ、プレイヤー2があと\(m\)ステップでゴールする状態を\((n,m)\)（ \(1 \leq n,m \leq N\)）で表す。状態\((n,m)\)で、どちらかのプレイヤーが勝つと状態が遷移し、あいこだと同じ状態に留まる。たとえば状態\((10,9)\)のとき、プレイヤー1がパーで勝てば状態\((8,9)\)に遷移する。
状態\((n,m)\)でプレイヤーが直面するゲームのナッシュ均衡（マキシミニ戦略でもある）における、プレイヤー1の期待利得（ゲームの値）を\(v_{n,m}\)とする。
\(n=0,-1\)または\(m=0,-1\)の場合にはゲームが決着し値が定まっている。これが再帰的に問題を解く初期状態となる。すなわち
\( \begin{align}
v_{0,m}=v_{-1,m}=1 & v_{n,0}=v_{n,-1}=-1 \tag{1}
\end{align} \)
（\(1 \leq n,m \leq N\)）とする。
このとき状態\((n,m)\)におけるゲームのプレイヤー1の利得は、以下の表となることが分かる。
零和ゲームであることから、プレイヤー2の利得は、上記行列に-1を乗じたものとなる。
ゲーム\((n,m)\)のプレイヤー1の均衡戦略とゲームの値\(v_{n,m}\)を求める。なお、ここでプレイヤー2の戦略は、状態\((m,n)\) でのプレイヤー1の戦略と同じになる。
プレイヤー1が均衡において、G,C,Pを出す確率（混合戦略）を\(q_G,q_C,q_P\)とする。このときプレイヤー2がG,C,Pを出したときのプレイヤー1の期待利得を\(E_G,E_C,E_P\)とすると、
\( \begin{align}
E_G=q_Gv_{n,m}+q_Cv_{n,m-1}+q_Pv_{n-2,m} \\
E_C=q_Gv_{n-1,m}+q_Cv_{n,m}+q_Pv_{n,m-2} \\
E_P=q_Gv_{n,m-2}+q_Cv_{n-2,m}+q_Pv_{n,m}
\end{align} \)
となる。
ここでナッシュ均衡では
\[
E_G=E_C=E_P=v_{n,m} \tag{2}
\]
が成立する。
上記の理由を正確に説明すると長くなるため端折って説明する。このゲームには、純粋戦略のナッシュ均衡はない。そして、これから１つの戦略に確率0を割り当てる（つまり2つの戦略のみに確率を割り当てる）ような混合戦略を用いたナッシュ均衡が存在しないことも分かる。ナッシュ均衡は必ず存在するので、このゲームにはすべての戦略に正の確率を割り振るような混合戦略（完全混合戦略と呼ぶ）のナッシュ均衡しかないことが分かる。
このゲームは零和ゲームであるたｍ、\(E_G,E_C,E_P\)はプレイヤー２がG,C,Pを出したときのプレイヤー1の期待利得であると同時に、プレイヤー２の期待利得に-1をかけたものとなる。もし均衡において\(E_G=E_C=E_P\)でなければ、プレイヤー２はこの値が最も高くなる戦略（G,C,Pのどれか）に確率0を割り当てることが最適反応戦略となる（最も高くなる戦略が２つある場合は、２つに0を割り振る）。これは上記の完全混合戦略しかナッシュ均衡がないことに矛盾する。これから\(E_G=E_C=E_P\)が得られて、期待利得\(v_{n,m}\)もこれと等しくなることが分かる。これより式(2)を得る。
ナッシュ均衡において、正の確率が割り振られる純粋戦略の期待利得はすべて等しくなる説明はこちら（混合戦略なッシュ均衡の求め方）も参照。
式(2)に対して、式(1)を初期条件として用いて、\(q_G,q_C,q_P\)と\(v_{n,m}\)を求めることで、再帰的に期待利得\(v_{n,m}\)と均衡戦略を求めることができる。しかしこの方程式は\(v_{n,m}\)に関ずる非線形方程式（３次方程式）になるため、数値的に解くこととする。
なお\(q_G,q_C,q_P\)はプレイヤー２の均衡戦略であるが（ナッシュ均衡は、プレイヤー１の期待利得を考えることで、プレイヤー２の戦略が求められる、こちらを参照）、\(n\)と\(m\)を入れ替えてプレイヤー１の戦略を求める。
まずプレイヤー１の期待利得について、基本的な確認をしてみる。
図１は、プレイヤー２のゴールまでステップ数\(m\)を横軸に取り、プレイヤー１のゴールまでのステップ数\(n\)ごとにプレイヤー１の期待利得を示したものである（\(n=1\dots,10\)）。
プレイヤー１の期待利得を\(v\)とするとき、プレイヤー１の勝利確率\(p\)は
\[ p=\frac{1}{2}\left(v+1\right) \]
で与えられるので、図1はプレイヤー１が勝利確率と考えることもできる。
表１はプレイヤー１の勝利確率である。例えば自分があと１ステップ（３歩）でゴールでき、相手が２ステップ（６歩）のとき（(n=1,m=2)）、相手はチョキかパーで勝てば逆転勝利できる位置にあるが、自分の勝利確率は63%(2/3)、相手は37%(1/3)である。
これらから、次のことが確認できる。
次に戦略について見ていこう。計算から次のようなことが分かった。
これらはたぶん均衡を求める式を丁寧に調べると証明できるのであろうが、やっていない。
さて、図２は\(m=1\)（プレイヤー２があと１ステップでゴールするとき） の両プレイヤーの戦略を、プレイヤー１の位置\(n\)を横軸としてグラフにしたものである。このゲームの特徴がよく現れている。
先に予想したとおり、２人ともあと１ステップでゴールできる場合（ \(n=m=1\)）では、G,C,Pを出す確率は\(1/3\)となり、普通のじゃんけんと同じになることが分かる。それ以外では、プレイヤー１はグーを出す確率が高く、プレイヤー２はチョキを出す確率が高い。プレイヤー２はあと１ステップでゴールできるので、グーよりもチョキやパーを出すことで有利にならないため、相手に２ステップ進ませることを何としても避けたい。そのためチョキを出してプレイヤー１がチョキやパーで進むことを阻止したいわけだ。プレイヤー１はそれを読み込むと、グーを出す確率を高くして、１ステップだけ進んでおこうとして、それが均衡となる。プレイヤー１の位置が２ステップのとき\(n=1,m=2\)では、それが最も顕著に現れ（プレイヤー２は１ステップでゴールできるにも関わらず、プレイヤー１に２ステップ進まれると逆転負けする）、プレイヤー１がグーを出す確率（＝プレイヤー２がチョキを出す確率）は0.52にまで上昇する。
図３は\(m=5\)（プレイヤー２があと５ステップでゴールするとき） のグラフである。
この例から分かるように、均衡戦略は次の２つの要因に影響される。
(1)ゴールまでの距離：プレイヤー１がゴールから離れるほど、グーを出す確率が増加しチョキを出す確率が減少する（プレイヤー２はチョキを出す確率が増加し、グーを出す確率が減少する）。 プレイヤー１がゴールから遠いとき、プレイヤー２はプレイヤー１が２ステップ進むことを避けるためチョキを出す確率を高め、それをプレイヤー１が読み込みグーを出す確率が高くなることを表している。相手がゴールより遠いときには逆転させないように１ステップづつ進ませる（自分がゴールから遠いときには１ステップづつ進む）戦略となる。同じ位置 \(n=m\) にいるときはグーとチョキを出す確率が同じになるので、基本的には勝っているときはチョキを出す確率が高く、負けているときはグーを出す確率が高くなる。
(2)奇数と偶数ステップの効果：プレイヤー１は偶数ステップではグーを出す確率が増加し、チョキを出す確率が減少する。先に見たようにプレイヤー１が残り２ステップでゴールする場合\(n=2\)、プレイヤー２はプレイヤー１が２ステップ進んで一気にゴールすることを阻止するためチョキを出す確率を高めるので、プレイヤー１はそれを読み込んでグーを出す確率を高める。これと同様の理由が再帰的に続くと考えられる。例えばプレイヤー１が残り３ステップと４ステップのときを考えると、どちらも１回ではゴールできず、少なくとも２回で勝たなければゴールできない。プレイヤー１が残り４ステップのとき、一気に２ステップ進まれると、残り１回で勝つチャンスがプレイヤー１に生まれるが、１ステップでは少なくともあと２回勝たなければダメなままである。これに対しプレイヤー１が残り３ステップのときは、１ステップ進んでも、２ステップ進んでも残り１回で勝つチャンスがプレイヤー１に生まれる。つまりプレイヤー２としては、プレイヤー１が偶数ステップのときに２ステップ進むことを阻止したいインセンティブが強くなる。それをプレイヤー１が読み込む結果だと思われる。
上記の２つの要因によって図3の戦略は解釈できると思われる。
最後の結果から、巷で言われる(?)図１の左側の利得行列の計算も、あながち間違っているわけではないと言える。
以上、グリコ、チョコレート、パイナップルの解をゲーム理論で解析した。なおこの確率はナッシュ均衡の確率を計算したものであり、相手がナッシュ均衡に従わない場合は必勝戦略とならないことに注意したい。例えば、チョキばかり出してくる馬鹿な相手に、上記の結果のナッシュ均衡戦略で勝負するよりは、グーを出したほうが良い。
この混合戦略のナッシュ均衡は、自分がナッシュ均衡に従っているならば、相手が何を出して来ようが、均衡における自分の期待確率を同じにしていることに注目したい。つまり自分が勝っているとき（相手よりも先に進んでいるとき）は均衡に従えば、相手が何を出そうが自分の有利さをそのまま保つことができる。これに対し、自分が負けているとき（相手が先に進んでいるとき）は均衡に従うと、相手が何を出しても自分の不利さをそのまま保つような戦略になってしまっている。そこで実践的な意味では、自分が先に進んでいるときは上記の確率に従い、負けているときは相手が均衡戦略から外れ、デタラメに出すことを期待して他の戦略を用いたほうが良いだろう。上記の偶数・奇数ステップでの知見を逆手に取り、自分が偶数ステップにいるときチョキの確率を高めて、２ステップ進む確率を高めたほうが良いかもしれない。
混合戦略のナッシュ均衡が何を意味しているのかは、混合戦略の項に少し記したが、私自身も理解していないことがいくつかある。これらは機会を見て、追加していきたい。