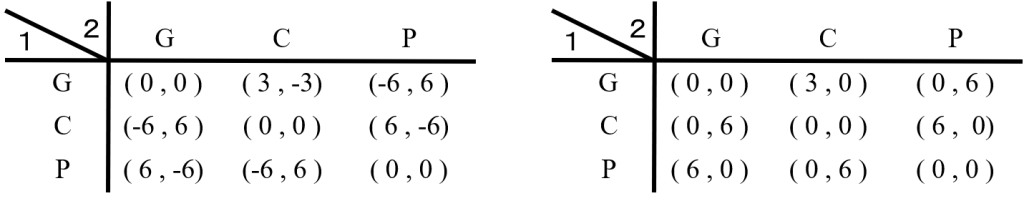グリコ(グリコじゃんけん)は「勝ち」と「負け」しかないのに、3点や6点の得点を割り当てて誤って計算されている答が多く、ゲーム理論として正しく解かれたものは(自分が知る限り)存在しない。ここでは 「グリコ・パイナップル・チョコレート」ゲームの正しい解について分析する。
このゲームは古くから知られていて、今でも子どもたちが遊んでいるのを見かける。多くの者の興味を引くようで、考察しているホームページや文献はいくつかあるが、どれも正しくない。…ということで、2019年度の渡辺ゼミの卒論で上野陽菜さんがこの問題に取り組んでくれたので、以下に発表。
本来は日本OR学会の2020年春季研究発表会で発表する予定であったが、コロナウィルス問題で学会が中止になったためここに公開。
結果の要旨を先にまとめると:
- 相手と自分が立っている位置によって戦略は異なる。例えば、両方があと3歩でゴールできる場合は(3歩でも6歩でもゴールするので)普通のじゃんけんと同じになり、グー・チョキ・パーを1/3ずつ出すことが均衡になる。
- 一方が他方よりゴールに近い場合、ゴールにより近い(つまり勝っている)プレイヤーは相手を6歩で勝たせる確率を少なくしようとしてチョキを多めに出す。これに対してゴールからより遠い(つまり負けている)プレイヤーはグーを出す確率を多めにして、少しずつ進む戦略を選ぶことが均衡となる。
- 両者がスタート地点にいるとき、スタート地点が遠くなると均衡戦略は、巷でよく計算される「グー・チョキ・パーを2:2:1で出すこと」( グー、チョキ、パーを3点、6点、6点で換算した1回のゲームの均衡戦略)に近づく。
はじめに
「グリコ・パイナップル・チョコレート」はスタート地点からじゃんけんをして、グー(以下G)で勝てば「グリコ」で3歩進み、チョキ(以下C)かパー(以下P)で勝てば「チヨコレイト」「パイナツプル」で6歩進んで、先にゴールしたほうが勝ち、というゲームである。古くから知られていて、私が子供の頃、50年くらい前には既に存在していたが、今でも子どもたちが遊んでいるのを見かける。この記事では、この「グリコ・チョコレート・パイナップル」ゲームの2人のときのゲーム理論における解を解析する。
もし、この2人ゲームの利得行列を図1の左側(進む歩数、進まれた歩数が利得)と考えるならば、ナッシュ均衡(零和ゲームなのでマキシミニ戦略と同じ)は「G,C,Pを2/5、2/5、1/5(2:2:1)で出す」ことが解になる。(求め方はいろいろなところに書いてある、例えばwikipedia) また右側と考えるならば「G,C,Pを1/4,1/2,1/4で出す」ことが解になる。
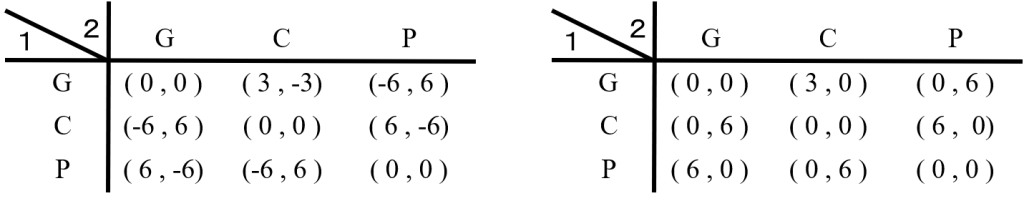 図1:誤った利得行列の例
図1:誤った利得行列の例
ちなみに右側は拙著「ゼミナールゲーム理論入門」に載っていて、求め方も(丁寧に)解説している。初心者にゲーム理論への興味を湧かせるために、このような例を用いたのだが、いつの間にかこの例が広まってしまった。中には「この解はおかしい」という人まで現れた。いやね、おかしいのは分かってて「このような利得だと考えると」と注意をしているのに…。失敗だった。いつか、これを正しておかなければ死ねないと、ずっと思っていた。本稿を仕上げることで、やっと死ねる。
図1のようなモデル化は間違っている。誤りの1つ目の点は、このゲームは元々「先にゴールしたほうが勝ち」というルールであり結果は「勝ち」「負け」しかなく、進んだ歩数が利得ではないからである。3とか6などの数値には正確な意味がなく、勝つか負けるかしかなく、勝ちは+1、負けは-1というゲームになるはずだ。
もう1つ上記のモデルが誤っている点、見落としている点は、このゲームは相手と自分が立っている位置によって、戦略が異なるということである。これを確認するには2人ともあと三歩以内でゴールできるという状態を想定すれば良い。このときは3歩でも6歩でもゴールできるので、G,C,Pは同じ効果を持つ(与える利得は同じ)。このときのナッシュ均衡は普通のじゃんけんと同じ「G,C,Pを1/3ずつ出す」となることは明らかだ。すなわち、このゲームにおける均衡戦略は「お互いが、あと何歩でゴールできるか」という状態に依存する。
ここではゲームを「先にゴールすれば勝ち、ゴールされれば負け」と考え、「勝てば利得が1、負ければ利得が-1」の2人零和ゲームと考える。そして2人のゴールまでの距離を状態変数としたゲーム(マルコフゲーム)と捉え、定式化して分析する。
問題のモデル化
このゲームを2人零和ゲームと考え、以下のようにモデル化する。
- 計算を単純にするため、3歩を1ステップと考える。
- 2人のプレイヤーが、ゴールのNステップ前の距離からじゃんけんをはじめ、Gで勝つと1ステップ、C,Pで勝つと2ステップ進む。あいこだと、どちらも進まない。
- 先にどちらかがゴールすればゲームが終了する。先にゴールした方は勝ちで利得1を獲得し、ゴールされた方は負けで利得-1とする。
- 「行き過ぎ」は考えない。ピッタリゴールしなくても勝ちとする。例えば1ステップ前からCで2ステップ進んでも、勝利とする。
- 時間経過による利得の割引は考えない。
プレイヤー1が、あと\(n\)ステップ、プレイヤー2があと\(m\)ステップでゴールする状態を\((n,m)\)( \(1 \leq n,m \leq N\))で表す。状態\((n,m)\)で、どちらかのプレイヤーが勝つと状態が遷移し、あいこだと同じ状態に留まる。たとえば状態\((10,9)\)のとき、プレイヤー1がパーで勝てば状態\((8,9)\)に遷移する。
状態\((n,m)\)でプレイヤーが直面するゲームのナッシュ均衡(マキシミニ戦略でもある)における、プレイヤー1の期待利得(ゲームの値)を\(v_{n,m}\)とする。
\(n=0,-1\)または\(m=0,-1\)の場合にはゲームが決着し値が定まっている。これが再帰的に問題を解く初期状態となる。すなわち
\( \begin{align}
v_{0,m}=v_{-1,m}=1 & v_{n,0}=v_{n,-1}=-1 \tag{1}
\end{align} \)
(\(1 \leq n,m \leq N\))とする。
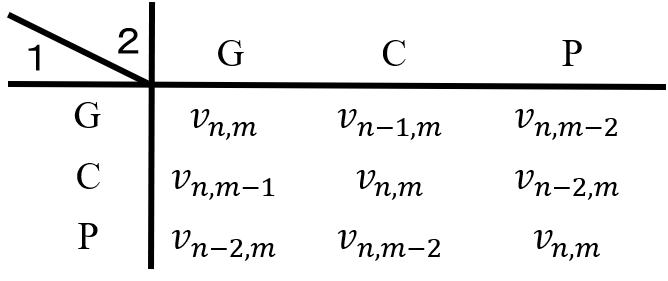
このとき状態\((n,m)\)におけるゲームのプレイヤー1の利得は、以下の表となることが分かる。
 状態(\(n,m\))におけるプレイヤー1の利得表
状態(\(n,m\))におけるプレイヤー1の利得表 零和ゲームであることから、プレイヤー2の利得は、上記行列に-1を乗じたものとなる。
問題の解法
ゲーム\((n,m)\)のプレイヤー1の均衡戦略とゲームの値\(v_{n,m}\)を求める。なお、ここでプレイヤー2の戦略は、状態\((m,n)\) でのプレイヤー1の戦略と同じになる。
プレイヤー1が均衡において、G,C,Pを出す確率(混合戦略)を\(q_G,q_C,q_P\)とする。このときプレイヤー2がG,C,Pを出したときのプレイヤー1の期待利得を\(E_G,E_C,E_P\)とすると、
\( \begin{align}
E_G=q_Gv_{n,m}+q_Cv_{n,m-1}+q_Pv_{n-2,m} \\
E_C=q_Gv_{n-1,m}+q_Cv_{n,m}+q_Pv_{n,m-2} \\
E_P=q_Gv_{n,m-2}+q_Cv_{n-2,m}+q_Pv_{n,m}
\end{align} \)
となる。
ここでナッシュ均衡では
\[
E_G=E_C=E_P=v_{n,m} \tag{2}
\]
が成立する。
上記の理由を正確に説明すると長くなるため端折って説明する。このゲームには、純粋戦略のナッシュ均衡はない。そして、これから1つの戦略に確率0を割り当てる(つまり2つの戦略のみに確率を割り当てる)ような混合戦略を用いたナッシュ均衡が存在しないことも分かる。ナッシュ均衡は必ず存在するので、このゲームにはすべての戦略に正の確率を割り振るような混合戦略(完全混合戦略と呼ぶ)のナッシュ均衡しかないことが分かる。
このゲームは零和ゲームであるたm、\(E_G,E_C,E_P\)はプレイヤー2がG,C,Pを出したときのプレイヤー1の期待利得であると同時に、プレイヤー2の期待利得に-1をかけたものとなる。もし均衡において\(E_G=E_C=E_P\)でなければ、プレイヤー2はこの値が最も高くなる戦略(G,C,Pのどれか)に確率0を割り当てることが最適反応戦略となる(最も高くなる戦略が2つある場合は、2つに0を割り振る)。これは上記の完全混合戦略しかナッシュ均衡がないことに矛盾する。これから\(E_G=E_C=E_P\)が得られて、期待利得\(v_{n,m}\)もこれと等しくなることが分かる。これより式(2)を得る。
ナッシュ均衡において、正の確率が割り振られる純粋戦略の期待利得はすべて等しくなる説明はこちら(混合戦略なッシュ均衡の求め方)も参照。
式(2)に対して、式(1)を初期条件として用いて、\(q_G,q_C,q_P\)と\(v_{n,m}\)を求めることで、再帰的に期待利得\(v_{n,m}\)と均衡戦略を求めることができる。しかしこの方程式は\(v_{n,m}\)に関ずる非線形方程式(3次方程式)になるため、数値的に解くこととする。
なお\(q_G,q_C,q_P\)はプレイヤー2の均衡戦略であるが(ナッシュ均衡は、プレイヤー1の期待利得を考えることで、プレイヤー2の戦略が求められる、こちらを参照)、\(n\)と\(m\)を入れ替えてプレイヤー1の戦略を求める。
計算結果
まずプレイヤー1の期待利得について、基本的な確認をしてみる。
図1は、プレイヤー2のゴールまでステップ数\(m\)を横軸に取り、プレイヤー1のゴールまでのステップ数\(n\)ごとにプレイヤー1の期待利得を示したものである(\(n=1\dots,10\))。
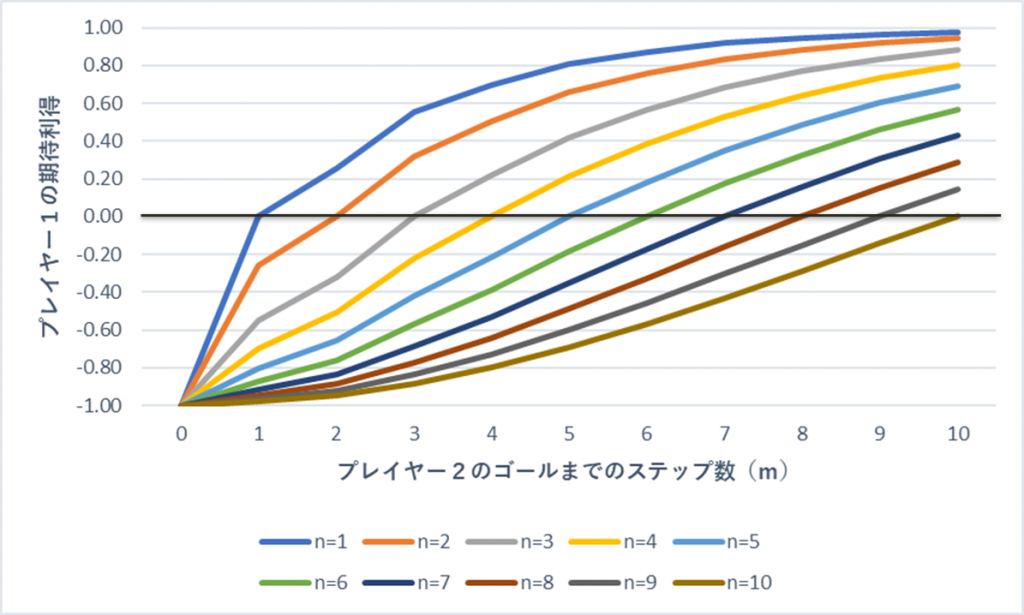 図1:プレイヤー1の期待利得(プレイヤー1の勝つ確率と同じ)
図1:プレイヤー1の期待利得(プレイヤー1の勝つ確率と同じ)
プレイヤー1の期待利得を\(v\)とするとき、プレイヤー1の勝利確率\(p\)は
\[ p=\frac{1}{2}\left(v+1\right) \]
で与えられるので、図1はプレイヤー1が勝利確率と考えることもできる。
表1はプレイヤー1の勝利確率である。例えば自分があと1ステップ(3歩)でゴールでき、相手が2ステップ(6歩)のとき((n=1,m=2))、相手はチョキかパーで勝てば逆転勝利できる位置にあるが、自分の勝利確率は63%(2/3)、相手は37%(1/3)である。
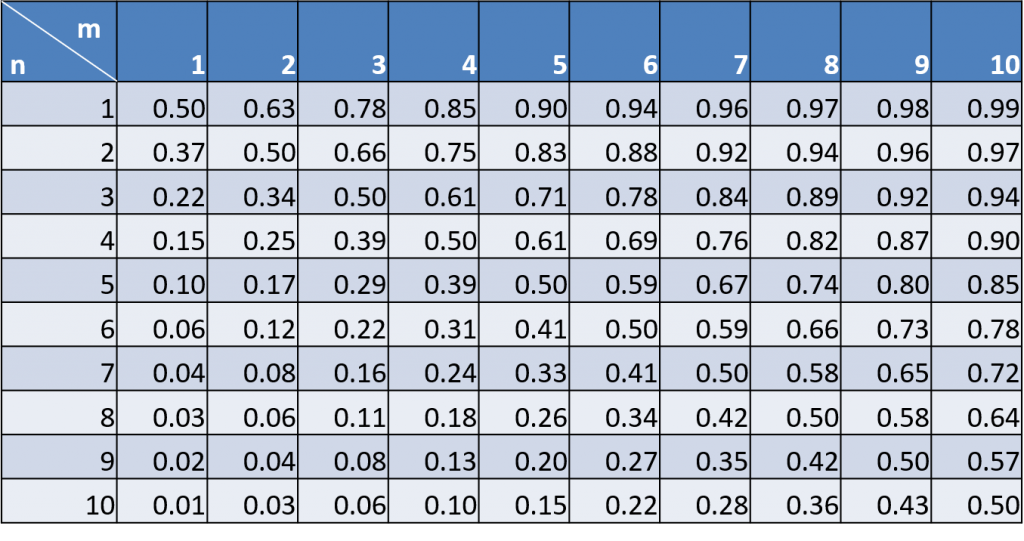 表1:プレイヤー1の勝利確率
表1:プレイヤー1の勝利確率
これらから、次のことが確認できる。
- プレイヤー1もプレイヤー2も同じ位置にいるとき(\(n=m\))、プレイヤーの勝つ確率は同じ(期待利得は0、 勝つ確率は0.5で等しい)。
- プレイヤー1の位置を固定すると(\(n\)のグラフを固定)、プレイヤー2の位置がゴールから遠くなればなるほど(\(m\)が増加するほど)、プレイヤー1の勝利確率は高くなり、
- プレイヤー2の位置を固定すると(\(m\)の値を固定)、プレイヤー1の位置がゴールから遠くなればなるほど(\(n\)が増加するほど)、プレイヤー1の勝利確率は低くなる。
次に戦略について見ていこう。計算から次のようなことが分かった。
- プレイヤー1の戦略に対し、グーとチョキを入れ替えるとプレイヤー2の戦略となる。パーの戦略は同じになる。
- パーを出す確率は、グーやチョキよりも低い。グーとチョキのどちらが高いかは、状態によって変化する
これらはたぶん均衡を求める式を丁寧に調べると証明できるのであろうが、やっていない。
さて、図2は\(m=1\)(プレイヤー2があと1ステップでゴールするとき) の両プレイヤーの戦略を、プレイヤー1の位置\(n\)を横軸としてグラフにしたものである。このゲームの特徴がよく現れている。
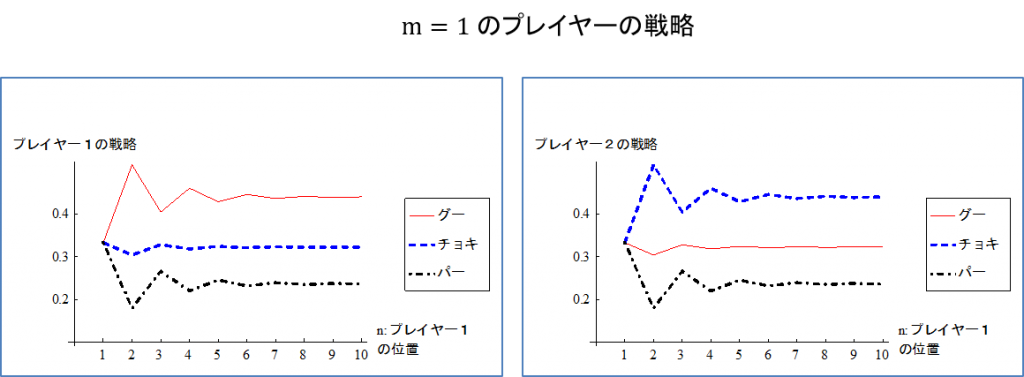 図2:あと1ステップ(3歩)でプレイヤー2がゴールするとき
図2:あと1ステップ(3歩)でプレイヤー2がゴールするとき
先に予想したとおり、2人ともあと1ステップでゴールできる場合( \(n=m=1\))では、G,C,Pを出す確率は\(1/3\)となり、普通のじゃんけんと同じになることが分かる。それ以外では、プレイヤー1はグーを出す確率が高く、プレイヤー2はチョキを出す確率が高い。プレイヤー2はあと1ステップでゴールできるので、グーよりもチョキやパーを出すことで有利にならないため、相手に2ステップ進ませることを何としても避けたい。そのためチョキを出してプレイヤー1がチョキやパーで進むことを阻止したいわけだ。プレイヤー1はそれを読み込むと、グーを出す確率を高くして、1ステップだけ進んでおこうとして、それが均衡となる。プレイヤー1の位置が2ステップのとき\(n=1,m=2\)では、それが最も顕著に現れ(プレイヤー2は1ステップでゴールできるにも関わらず、プレイヤー1に2ステップ進まれると逆転負けする)、プレイヤー1がグーを出す確率(=プレイヤー2がチョキを出す確率)は0.52にまで上昇する。
図3は\(m=5\)(プレイヤー2があと5ステップでゴールするとき) のグラフである。
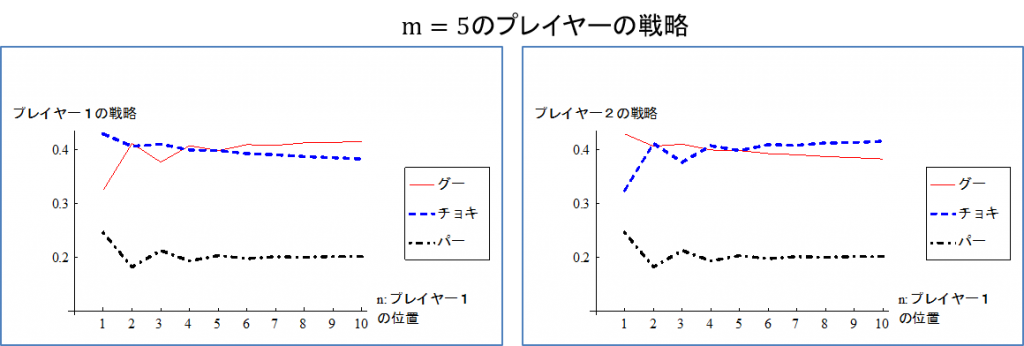 図2:あと5ステップ(15歩)でプレイヤー2がゴールするとき
図2:あと5ステップ(15歩)でプレイヤー2がゴールするとき
この例から分かるように、均衡戦略は次の2つの要因に影響される。
(1)ゴールまでの距離:プレイヤー1がゴールから離れるほど、グーを出す確率が増加しチョキを出す確率が減少する(プレイヤー2はチョキを出す確率が増加し、グーを出す確率が減少する)。 プレイヤー1がゴールから遠いとき、プレイヤー2はプレイヤー1が2ステップ進むことを避けるためチョキを出す確率を高め、それをプレイヤー1が読み込みグーを出す確率が高くなることを表している。相手がゴールより遠いときには逆転させないように1ステップづつ進ませる(自分がゴールから遠いときには1ステップづつ進む)戦略となる。同じ位置 \(n=m\) にいるときはグーとチョキを出す確率が同じになるので、基本的には勝っているときはチョキを出す確率が高く、負けているときはグーを出す確率が高くなる。
(2)奇数と偶数ステップの効果:プレイヤー1は偶数ステップではグーを出す確率が増加し、チョキを出す確率が減少する。先に見たようにプレイヤー1が残り2ステップでゴールする場合\(n=2\)、プレイヤー2はプレイヤー1が2ステップ進んで一気にゴールすることを阻止するためチョキを出す確率を高めるので、プレイヤー1はそれを読み込んでグーを出す確率を高める。これと同様の理由が再帰的に続くと考えられる。例えばプレイヤー1が残り3ステップと4ステップのときを考えると、どちらも1回ではゴールできず、少なくとも2回で勝たなければゴールできない。プレイヤー1が残り4ステップのとき、一気に2ステップ進まれると、残り1回で勝つチャンスがプレイヤー1に生まれるが、1ステップでは少なくともあと2回勝たなければダメなままである。これに対しプレイヤー1が残り3ステップのときは、1ステップ進んでも、2ステップ進んでも残り1回で勝つチャンスがプレイヤー1に生まれる。つまりプレイヤー2としては、プレイヤー1が偶数ステップのときに2ステップ進むことを阻止したいインセンティブが強くなる。それをプレイヤー1が読み込む結果だと思われる。
上記の2つの要因によって図3の戦略は解釈できると思われる。
- \(n=m=1\)ではG,C,Pを出す確率は\(1/3\)となる。
- \(n=m\)ではグーとチョキを出す確率が同じ。
- \(n=m\)として、\(n,m\)を大きくすると、均衡戦略は図1の左側の利得行列のナッシュ均衡である\(2/5,2/5,1/5\)に近づくことが分かる。すなわち両者がスタート地点にいるとき、スタート地点が遠いならば「グー・チョキ・パーを2:2:1で出す」ことが均衡戦略となる。
最後の結果から、巷で言われる(?)図1の左側の利得行列の計算も、あながち間違っているわけではないと言える。
まとめ
以上、グリコ、チョコレート、パイナップルの解をゲーム理論で解析した。なおこの確率はナッシュ均衡の確率を計算したものであり、相手がナッシュ均衡に従わない場合は必勝戦略とならないことに注意したい。例えば、チョキばかり出してくる馬鹿な相手に、上記の結果のナッシュ均衡戦略で勝負するよりは、グーを出したほうが良い。
この混合戦略のナッシュ均衡は、自分がナッシュ均衡に従っているならば、相手が何を出して来ようが、均衡における自分の期待確率を同じにしていることに注目したい。つまり自分が勝っているとき(相手よりも先に進んでいるとき)は均衡に従えば、相手が何を出そうが自分の有利さをそのまま保つことができる。これに対し、自分が負けているとき(相手が先に進んでいるとき)は均衡に従うと、相手が何を出しても自分の不利さをそのまま保つような戦略になってしまっている。そこで実践的な意味では、自分が先に進んでいるときは上記の確率に従い、負けているときは相手が均衡戦略から外れ、デタラメに出すことを期待して他の戦略を用いたほうが良いだろう。上記の偶数・奇数ステップでの知見を逆手に取り、自分が偶数ステップにいるときチョキの確率を高めて、2ステップ進む確率を高めたほうが良いかもしれない。
混合戦略のナッシュ均衡が何を意味しているのかは、混合戦略の項に少し記したが、私自身も理解していないことがいくつかある。これらは機会を見て、追加していきたい。
じゃんけん研究