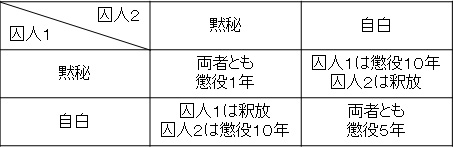
調整ゲームはコーディネーションゲーム(coordination game)の翻訳で、協調ゲームと訳されることもあります。ざっくり言うと「他人と同じ行動を選ぶことが良い」ようなゲームです。結果となるナッシュ均衡は「全員が同じ行動を選ぶ」となるので(確率を用いる混合戦略を除く)、結果の候補が複数あることになります(複数均衡)。
女と男の戦い
ゲーム理論で最初に習う2人調整ゲームは、 以下のストーリーで表される女と男の戦い(battle of sexes)です(変な名前!でも昔は「両性の戦い」と訳されていました。これだとさらに意味不明です)。
アリスと文太は、禅寺かショッピングセンターに行く。2人は相手の行動を知らずに、どちらに行くかを選ぶ。アリスと文太は、お互いが好意を抱いているので同じ場所を選べば利得1を獲得し、さらにそれが自分が好きな場所ならば利得にもう1点が加わり2になる。違う場所を選んでしまうと(たとえ好きな場所に行ったとしても)利得は0である。
「女と男がいて、お互い同じ場所に行きたい。できれば自分の行きたいところがいい!」というそれだけのゲームです。男女が武闘しているわけではありません。この状況を利得行列 にすると、以下のようになります。
女と男の戦い(battle of sexes) この状況では、各プレイヤー(アリスと文太)はそれぞれ
調整ゲームの例
どのSNSに参加するか、という問題。自分の友人が皆んなFaceBookを選んでいるならばFBを、インスタグラムを選んでいるならインスタを選ぶことが良い。このように商品に正の外部性(自分が購入する財から得る効用は、他の消費者がそれを多く選んでいるほど高くなる)があるときの消費者の選択は調整ゲームになります。 技術規格のデファクトスタンダード問題。かつてビデオデッキの開発において、各企業はVHS方式とベータ方式のどちらの規格を選ぶかという問題に直面しました。企業の選択は、多くの企業が選択するものと同じ規格を選択したほうが有利になります(wikipedia デファクトスタンダード ) 同窓会の参加。皆んなが参加するならば、自分も参加したほうが良いけど、皆んなが参加しないなら、自分も参加しないほうが良い。 右側通行か左側通行か。細い道を車ですれ違うとき、右に避けるか左に避けるか。お互いに右か左か同じルールを選ばないと衝突してしまう。 調整ゲームのバリエーション
先ほどの「女と男の戦い」では、相手と同じ行動を選ぶことが良いわけですが、各プレイヤーは、どの結果が最良であるかが異なっています。アリスにとっては2人が禅を選ぶことが、文太には2人がショッピングを選ぶことが良いわけです。このような調整ゲームは非対称(asymmetric)であると言われます。これに対して「どの結果でも、2人が会えさえすれば同じ(1点)」のように、結果に差がなく、行動が一致さえすれば良いゲームは対称(symmetric)な調整ゲーム、純粋調整ゲーム(pure coordination game)、またはマッチングゲーム(matching game)と呼ばれます(Camerar 2003)。
2人とも買い物が好きで、禅寺で会えれば1点、ショッピング・センターで会えれば2点、のようなゲームも考えられます。このゲームでは、行動が一致しないより一致したほうが良いのですが、一致したときに皆にとって利得が高い場合と低い場合があります。このようなゲームには、定着した呼び名はありません。ここではTremblay and Horton(2012)に従いパレート調整ゲーム(Pareto coordination game)と呼んでおきます。
調整ゲームのバリエーション 調整ゲームの解
調整ゲームでは、すべてのプレイヤーが同じ行動を選択すること がゲームの解であるナッシュ均衡 になります(他に確率を用いて選択を行う混合戦略のナッシュ均衡もあります)。例えば上述の女と男の戦いでは
(A)アリスも文太も禅寺に行く
という2つのナッシュ均衡があります(他に混合戦略のナッシュ均衡がある⇒最後の「注意点」を参照せよ)。実際にナッシュ均衡の求め方 にしたがって利得に下線を引くと以下の図となり、両プレイヤーの利得に下線が引いてある戦略の組は、上記の(A)と(B)であることが分かります。
女と男の戦いのナッシュ均衡 このように調整ゲームでは複数のナッシュ均衡 が存在し、その中でどれを起こりうる結果である「ゲームの解」とするのか、という問題が起きます。この問題は均衡選択の問題と呼ばれ、ゲーム理論の大きな研究テーマです。
このときその中の1つのナッシュ均衡が起きるとすべてのプレイヤーが共通な認識で予測できるような理由があるならば、それは解となりえます。このような皆が共通して結果として予測できるような点はフォーカルポイントと呼ばれます(Schelling (1960))。フォーカルポイントは、「社会慣習」や「これまで繰り返しプレイされてきて培われた経験」などによって形成されると言えます。
例えば上記の男と女の戦いでは、2人はいつも禅に行くことになっている(という慣習や経験があれば、2人は迷うことなく禅を選ぶでしょう。また、そのような経験がなくても「レディファースト」 (アリスに文太が譲る)という慣習があれば、やはり2人は禅を選ぶことになります。文太は、本当は2人でショッピングに行ったほうが良いのですが、アリスが禅に行くと予測するなら、ショッピングよりは禅が良い選択であり、アリスも文太が禅に行くと予測できるなら禅に行くことが良い選択です。つまりナッシュ均衡の定義である 「相手がそのナッシュ均衡の行動を選ぶなら、自分もそのナッシュ均衡の行動を選ぶことが一番良い」という条件を満たすことになります。
これに対して、上記のように2人が共通して予測できるフォーカルポイントがなければ、ナッシュ均衡は実現できるとは限りません。上記のようなゲームを実験室でやらせるとお互いが異なる行動を選び0点を食らってしまう結果も多く見られます。私も講義中にこの実験をやらせてみますが、うまくコーディネイトできるときもあれば、そうでない場合も多いです。うまくコーディネイトできない場合には、(当然ですが) 次の2つのパターンがあります:賢者の贈り物 」パターンと呼んでいます。)
パレート調整ゲームでは、一般的にはプレイヤーにとって利得が高い<良い>ナッシュ均衡(パレート優位な均衡と呼ばれる) が望ましく、単純に考えるとそれが実現されると予想されますが、何らかの理由で両者にとって利得が低い<悪い>ナッシュ均衡が実現することも、十分あり得ます。先ほどの例2だと、2人ともショッピングに行くことで利得2が達成できるためこれが<良い>ナッシュ均衡ですが、例えば2人とも毎週毎週ずーっと禅寺に行っていることが定着していて、「相手は禅寺に行く」「相手は自分も禅寺に行くと予想するだろう」と考えれば(2人ともショッピングに行くほうが楽しいと分かっていても)禅寺に行くと考えられます。
調整ゲームにおいて、ナッシュ均衡が実現しない問題、ナッシュ均衡が実現してもパレート優位なナッシュ均衡が実現しない問題は、調整の失敗(coordination failure)と呼ばれます。
フォーカルポイントの例
単純なマッチングゲームでは、さまざまなフォーカルポイントがあると予想されますSchelling(1960)は、以下のようなゲームを(インフォーマルに)実験したようです。
表(head)か裏(tail)のどちらかを選べ。2人が同じものを選んだら賞金をあげよう。 好きな正の番号を選べ。2人が同じものを選んだら賞金をあげよう。 ニューヨークのどこかで待ち合わせをする。どこで待ち合わせをするか選べ。 何を選んでも良いのですが、お互いに同じものを選ぶと良いので「調整ゲーム」であることが分かります。賞金に差もなく個人で選ぶと良いものに違いもないので、マッチングゲームですね。
Schelling(1960)によると最初のゲームでは42人中36人がheadを、2番めのゲームでは40%が「1」を選んだといいいます。3番めの質問では多数がGrand Central StationのInformation boothだとされています。
Mehta, Starmer and Sugden (1994)は、このような実験を精緻に行っています。この研究では被験者は2つのグループに分けられ、1つのグループC (Coordination)では「(ランダムに選ばれた)相手と同じものを選んだら賞金を与える」とされ、もう1つのグループP(Picking)では「何を選んでも賞金を与えるので、好きなものを選べ」としています。上記の最初の質問では、グループCでは87%、グループPでは76%がheadを選びそれほど差がないのに対して、2番めの質問では、グループCで選ばれたのは「1」が40%に選ばれて一番多く(「7」が2番めで14%)、グループPでは「7」が一番多く11%になっています。このことからある種の質問に対して、「自分が好きなもの」を選ぶのではなく「相手と同じものを選ぶためには何が良いか」を考えてそれを選ぶというフォーカルポイントが存在するということが分かります。
SchellingやMehta達は言及していないのですが、実験結果のデータを見て私が感じたのは「皆が同じものを選ぶと賞金をあげる」と言っているのに、自分が好きな数や場所を選ぶ被験者は、少数ながら必ずいるんだな…ということです。ルールが理解できていないのか、それとも何か意図があるのか.「フォーカルポイントに従う」という行動は、「大勢」や「傾向」ではありますが、それに逆らう(理解できない?従わない?)個の存在も無視できず、それはやはり「少数」や「個性」や「多様性」と言う社会科学の重要なテーマに繋がるのだな、と思いました。
注意点
ここでは2人ゲームと多人数のゲームを曖昧に扱ってきましたが、厳密には分けて考えることが必要です。 ここでは確率を使わない行動の選択(純粋戦略)のみを考えましたが、調整ゲームには各プレイヤーが確率を使って行動を選択する混合戦略を用いたナッシュ均衡もあります。例えば女と男の戦いの例だと「アリスは禅を2/3、ショッピングを1/3で選び、文太は禅を1/3、ショッピングを2/3で選ぶ」というナッシュ均衡があります。例1のマッチングゲームだと「アリスも文太も、禅とショッピングを1/2ずつ選ぶ」というナッシュ均衡があります。 相手と異なる行動を選ぶことが良いゲーム(チキンゲーム・混雑ゲーム)も広義の調整ゲームとみなされる場合があります。これはゲームの文脈を1回限りの2人のゲームと見做すか、多人数で長期間に渡って行われるゲームと考えるかで異なってきます。 調整ゲームにおいて「複数の均衡の中でどれが起きるか」という問題は、ゲーム理論における均衡選択という理論によって分析されており、リスク支配という概念によって起きる結果が選ばれます。 参考文献
Camerar (2003), Behavioral Game Theory: Experiments in Strategic Interaction, Princeton Univercity Press. Mehta, Starmer, Sugden (1994), The nature of salience: An experimental investigation of pure coordination games, The American Economic Review, Vol.84, No.3, pp.658-673. Schelling(1960), The strategy of conflict, Harvard Univercity Press. Tremblay and Tremblay (2012), New Perspectives on Industrial Organization: With Contributions from Behavioral Economics and Game Theory, Springer. 以下も参考にしてください。
東京都立大学 2020ゲーム理論1 オンライン講義(2020:コロナ対応)