昨年(2021年）の10月に東京都立大学のオープンユニバーシティで講義した「高校生のためのゲーム理論入門」（高校生のための大学授業体験シリーズ）の動画が、東京都立大学のホームページ内でOCWとして公開されることになりました！
2021年度東京都立大学オープンユニバーシティ・高校生のための大学授業体験シリーズ 高校生のためのゲーム理論入門
他のゲーム理論講義動画とともにどうぞ
ナッシュ均衡を計算するwebアプリ
2022年のお正月！ナッシュ均衡を計算するプログラム（webアプリ）を作成しました。2人戦略形ゲームのナッシュ均衡を（混合戦略まで含め）すべて計算するプログラムです（ただし戦略は10以下）。日本には、ありそうでないんじゃないか、と思います。ぜひ、使ってみてください。
NABENAVI.net 計算プロジェクト
戦略10以下の2人戦略形ゲームのナッシュ均衡を（混合戦略まで含めて）すべて計算するプログラムなど、趣味で作ったweb上の計算アプリケーションを提供しています。
- ナッシュ均衡計算プログラム
- 2人戦略形ゲームのナッシュ均衡を全列挙する計算アプリです（戦略は10以下）。
- 逆行列計算
- ナッシュ均衡の計算プログラムを作るときに、練習として作ったものです。
混合戦略ナッシュ均衡の求め方
ここでは２☓２ゲーム（プレイヤーが２人で戦略が２つ）の混合戦略のナッシュ均衡の求め方について記します。通常は最適反応戦略のグラフを書いて求めますが、ここではグラフを書かずに簡便な方法を考えていこうと思います。以下の関連投稿も参照して下さい。
- ナッシュ均衡の求め方：2人ゲームの利得行列の場合
- ２人ゲームでの（混合戦略ではない）純粋戦略のナッシュ均衡の求め方について記しています。
- ナッシュ均衡を計算するプログラム（webアプリ）
- 混合戦略まで含めてすべてのナッシュ均衡を計算するweb上のアプリケーションです。戦略が10以下までです。
- 混合戦略
- 混合戦略と混合戦略のナッシュ均衡とは何かについて書いています。
- ナッシュ均衡（ざっくりした説明）
- ナッシュ均衡とは何かについて、ざっくり記しています。
- グリコ・チョコレート・パイナップルの正しい解
- 混合戦略の真骨頂！
- 普通、講義で学ぶ「最適反応戦略のグラフ」を書く方法は、以下のオンライン講義を参考にすると良いでしょう。
２☓２ゲームの混合戦略ナッシュ均衡を求める
以下の２☓２ゲームの混合戦略のナッシュ均衡を求めてみます。
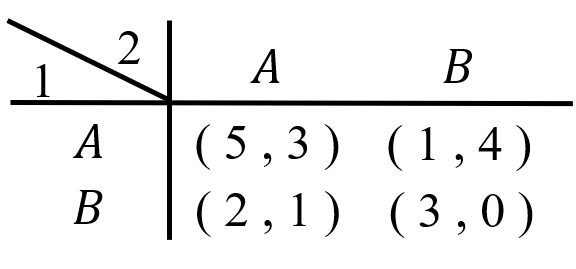
まず、プレイヤー１がAを選ぶ確率を\(p\)とします（Bを選ぶ確率は\(1-p\)となります）。次に、プレイヤー２がAを選ぶ確率を\(q\)とします（Bを選ぶ確率は\(1-q\)となります）。
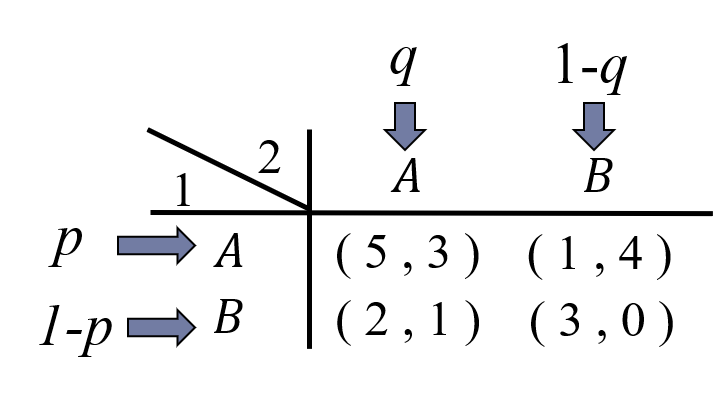
さて、プレイヤー１の戦略で\(p=1\)と\(p=0\)の混合戦略は、「Aを選ぶ」「Bを選ぶ」という純粋戦略と同等なので、ここでは求めるべきものから除外します。すなわちここでは「純粋戦略ではない混合戦略のナッシュ均衡」＝「すべての戦略を選ぶ確率が正である混合戦略のナッシュ均衡」を求めることとします。したがって\(0<p<1\)とします。同様にプレイヤー２に対しても\(0<q<1\)とします。
\(0<p<1\)、\(0<q<1\) のように「すべての戦略を選ぶ確率が正である混合戦略」は完全混合戦略(completely mixed strategy) と呼ばれます。
ここでプレイヤー１が戦略Aを選んだときの期待利得（利得の期待値）は
\[ q \times 5+(1-q) \times 1=4q+1 \tag{1} \]
であり、戦略Bを選んだときの期待利得（利得の期待値）は
\[ q \times 2 +(1-q) \times 3=-q+3 \tag{2} \]
です。 完全混合戦略であるためには、期待利得が等しくなければならないので（理由は後述）
\[4q+1=-q+3\]
でなければなりません。これを解いて\(q=2/5\)を得ます。
利得の期待値の計算については後ほど詳しく説明しています。
同様にプレイヤー２を考えます。 プレイヤー２が戦略Aを選んだときの期待利得（利得の期待値）は\( p \times 3+(1-p) \times 1=2p+1 \)であり、戦略Bを選んだときの期待利得（利得の期待値）は\( p \times 4 +(1-p) \times 0=4p \)です。やはり期待利得が等しくなければならないので、\(2p+1=4p\)でなければならず、これを解いて\(p=1/2\)を得ます。
以上のことより、混合戦略のナッシュ均衡は
プレイヤー１はAを\(1/2\)、Bを\(1/2\)で選び、プレイヤー２はAを\(2/5\)、Bを\(3/5\)で選ぶ (*)
となります。
このように２☓２ゲームで混合戦略のナッシュ均衡を求めるには、各プレイヤーの２つの戦略を選んだときの期待利得が等しくなるようにすれば良いです。「なぜそうなるのか？」「ナッシュ均衡における期待利得は？」「そもそも期待利得の計算って、どうするの？」について、次に考えてみます。
均衡で期待利得が等しい理由
そもそも「期待利得（利得の期待値）」からつまずいていることも多いので、プレイヤー１の期待利得について、少し詳しく説明します。各プレイヤーが\(p,q\)に従って戦略を選んだときに、戦略の組\((A,A),(A,B),(B,A),(B,B)\)が実現する確率は\(pq,p(1-q),(1-p)q,(1-p)(1-q)\)で、そのときに実現する利得は\(5,1,2,3\)です。これより混合戦略を用いたときのプレイヤー１の期待利得は
\[ pq \times 5+p(1-q) \times 1+(1-p)q \times 2+(1-p)(1-q) \times 3 \]
となります。なお前の２項を\(p\)で、後の２項を\(q\)でくくると期待利得は
\[p(-4q+1)+(1-p)(-q+3) \tag{3} \]
と書くこともできます（この式は後で使います）。
次に「プレイヤー１がAを選んだときの期待利得」です。プレイヤー１がAを選ぶ（確率ではなく確実に選ぶ）と、プレイヤー２がAを選ぶ確率は\(q\)、Bを選ぶ確率は\(1-q\)で、そのときの利得はそれぞれ1と5ですから、期待利得は式(1)のように計算できて\(4q+1\)となります。同様にプレイヤー１がBを選ぶと期待利得は式(2)のように計算できて\(-q+3\)となるわけです。
さてこれと式(3)を見比べると、式(3)は
\[ p \times（Aを選んだときの期待利得）+ (1-p) \times
（Bを選んだときの期待利得）\]
となっていることが分かります。つまり自分がA、Bを選ぶときの確率を\(p,1-p\)としたときの期待値は「期待利得の期待値」になっている訳です。
「期待利得の期待値」が、もともとの「期待値」と同じになることは「複合くじに関する公理」と呼ばれる仮定です。ここが成立しないと考える研究も存在します。
ナッシュ均衡では、与えられた\(q\)に対して、プレイヤー１は期待利得（＝式(3)）を最大にする確率\(p\)を選びます（最適反応戦略）。このとき\(4q+1>-q+3\)だと\(p=1\) 、\(4q+1<-q+3\)だと\(p=0\)が式(3)を最大にすることが分かります。高い期待値を与える戦略を確率１で選ぶことが自分にとっては良く、低い期待値を与える戦略にの戦略に少しでも確率を割り当てると利得は低くなってしまうのです。
しかし\(0<p<1\)でなければなりませんので、\(p=0,p=1\)ではいけません。このことから完全混合戦略であるためには、Aを選んだときの期待利得とBを選んだときの期待利得は等しくなければならず、\(4q+1=-q+3\)でなければならないのです。プレイヤー２についても同様です。
ナッシュ均衡における期待利得を求める
以上でナッシュ均衡が\(p=1/2\)、\(q=2/5\)と計算できることが分かりました。ここで\(4q+1=-q+3=A\)と置いてみると、式(3)は
\[pA+(1-p)A=A \tag{4} \]
となります。これからナッシュ均衡における期待利得は\(A\)であることが分かります。つまり混合戦略を用いたときの期待利得は、本来は式(3)に\(p,q\)の値を代入して求めなければならないのですが、ここでは\(p\)は必要なく、\(-4q+1\)か\(-q+3\)のどちらか（簡単な方）に\(q=2/5\)を代入するだけで良いことが分かります。これよりナッシュ均衡におけるプレイヤー１の期待利得は\(-q+3=13/5\)となることが分かります。同様にプレイヤー２のナッシュ均衡における期待利得は\(4p=2\)となります。
相手の利得が自分の戦略を決める
この計算方法は、解法を鵜呑みにするのではなく、その意味を考えると「本当にこれで良いのか？」と考えこんでしまいます（よね？？）。この計算方法では「相手が２つの戦略を選ぶ期待利得が等しくなるように、自分の戦略が決まる」からです。つまり端的には「相手の利得が自分の戦略を決める」「自分の利得は自分の混合戦略均衡を決めるために関係ない」ように見えるからです。
図３はここまでの例題とプレイヤー２の利得は同じであり、プレイヤー１の利得が定まっていないようなゲームです。この場合でも完全混合戦略があるとすれば、それは\(p=1/2\)となります。
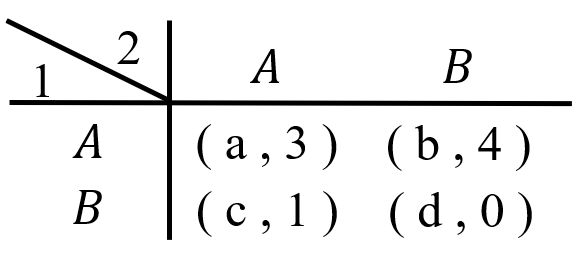
ただそれは「ナッシュ均衡でプレイヤー１が選ぶ戦略に、プレイヤー１の利得が全く関係ない」と言うわけではありません。例えば\(a=b=1,c=d=0\)では、プレイヤー１の支配戦略はAとなり、ナッシュ均衡も(A,B)となります（\(p=1,q=0\)）。つまり\(a,b,c,d\)が「完全混合戦略がナッシュ均衡となるような条件」(\((a-c)(b-d)<0\)) を満たさなければなりません 。
２☓２ゲームのナッシュ均衡をすべて求める
上記の方法は２☓２ゲーム（プレイヤーが２人で戦略が２つのゲーム）の完全混合戦略のナッシュ均衡を計算する方法です。しかし、この方法ではそれ以外＝「完全混合戦略ではないナッシュ均衡」は求められないため改めて注意が必要です。以下の図４の２つのゲームを見てみましょう。
図４の左側の例は図１の例題のゲームに、純粋戦略でのナッシュ均衡の求め方に従って最適反応戦略となる利得に下線を引いた図です。これから分かるように、このゲームには両プレイヤーの利得に下線が引かれる戦略の組はありません。すなわち、このゲームには、純粋戦略のナッシュ均衡がないのです。したがってこのゲームのナッシュ均衡は既に求めた完全混合戦略のナッシュ均衡が１つあるだけになります。
これに対して、図４の右側のゲームでは（A,A)（B,B)の両プレイヤーの利得に下線が引かれています。すなわちこのゲームでは（A,A)（B,B) という２つのナッシュ均衡があります。そして、さらに完全混合戦略のナッシュ均衡が１つあるのです。ここまでの方法に従って、その均衡を求めてみましょう。プレイヤー１がAを選ぶ確率を\(p\)（Bを選ぶ確率は\(1-p\)）、プレイヤー２がAを選ぶ確率を\(q\)（Bを選ぶ確率は\(1-q\)）とします。
プレイヤー１が戦略Aを選んだときの期待利得は\( q \times 2+(1-q) \times 0=2q\)
、戦略Bを選んだときの期待利得は\( q \times 0 +(1-q) \times 4=-4q+4\)
です。 期待利得が等しくなければならないので\(2q=-4q+4\)であることから、\(q=2/3\)を得ます。
同様にプレイヤー２を考えます。 プレイヤー２が戦略Aを選んだときの期待利得は\( p \times 3+(1-p) \times 0=3p\)で、戦略Bでは\( p \times 0 +(1-p) \times 1=1-p \)です。やはり期待利得が等しくなければならないので、\(3p=1-p\)でなければならず、これを解いて\(p=1/4\)を得ます。
これらを総合すると図４の右側のゲームのナッシュ均衡は
(1)プレイヤー１がA、プレイヤー２がAを選ぶ。（\(p=1,q=1\)に相当する ）
(2)プレイヤー１がAを1/4、Bを3/4で選び、プレイヤー２がAを2/3、Bを1/3で選ぶ。
（\(p=1/4,q=2/3\)に相当する ）
(3)プレイヤー１がB,プレイヤー２がBを選ぶ。（\(p=1,q=1\)に相当する ）
と３つあることになります。
2☓2ゲームのほとんどのゲーム（特殊な場合を除く）は、以下の4タイプに分けることができます。
(1)2人のプレイヤーとも、支配戦略がある（囚人のジレンマなど）
(2)1人のプレイヤーだけに支配戦略がある（合理的な豚など）
(3)プレイヤーに支配戦略がなく、純粋戦略のナッシュ均衡がある（調整ゲーム、チキンゲームなど。図４の右側のゲームがこれ）
(4) プレイヤーに支配戦略がなく、純粋戦略のナッシュ均衡もない（マッチングペニー、サッカーのPKのゲームなど。図１（図４左側）のゲームがこれ）
(1)と(2)には完全混合戦略のナッシュ均衡はなく、プレイヤーが支配戦略を使う純粋戦略のナッシュ均衡が１つあるだけです。ちなみにこれに対して上記の混合戦略のナッシュ均衡の求め方を用いると\(p\)や\(q\)が負になったり、１を超えたりします。上記の求め方で0や1を超える値が出たときは、支配戦略がないかもう一度チェックする必要があります。既に見たように(3)では3個、(4)では1個のナッシュ均衡があります。
したがってナッシュ均衡をすべて求めるためには(1)-(4)に留意して求める必要があります。２☓２のナッシュ均衡の解を求める、ここで述べた方法ではなく、最適反応戦略のグラフを書く方法が一般的で、その方法を使うと(1)-(4)まで包括的(?)に求めることができます。拙著ゼミナールゲーム理論入門などを参照して下さい。
すでに話したように「混合戦略まで含めると、ナッシュ均衡は必ず存在する」という定理がありますが、さらに加えて、ほとんどの場合にナッシュ均衡は奇数個であることも証明されています。「ほとんどの場合」というのは、例えば利得が全部同じ数だったりすると、あらゆる混合戦略がナッシュ均衡になったりするわけで、そういう特殊な場合を除く、ということです。「２次方程式の解は、ほとんどの場合２個である」というのと同じような意味です（重根の場合を除いている）。
まとめ
まとめると２☓２のナッシュ均衡を求めるには
STEP.1 まず純粋戦略のナッシュ均衡を求める。
STEP.2 (1)か(2)のタイプ、すなわち支配戦略がある場合は、それで終わり。完全混合戦略のナッシュ均衡はない。
STEP.3 (3)か(4)のタイプの場合は完全混合戦略のナッシュ均衡があるので、各プレイヤーが一方の戦略を選ぶ確率を\(p,q\)とそれぞれ置き、各プレイヤーが２つの純粋戦略を選んだときの期待利得を求める。
STEP.4 上記で求めた、各プレイヤーが２つの純粋戦略を選んだときの期待利得が等しくなるように\(p,q\)を定める。相手の期待利得が等しくなるように自分の混合戦略が決まることに注意する。
となります。以上、２☓２ゲームの混合戦略のナッシュ均衡の求め方について記してみました。こうしてみると、混合戦略のナッシュ均衡とは何なのか？と考える方も多いと思います。混合戦略のページに少しそれについて書きました。
注意点
- 式(4)から分かることをもう１つ。ナッシュ均衡では、プレイヤー１はどんなpを選んでも期待利得はAになります。これはナッシュ均衡では、プレイヤー１は何を選んでも最適反応戦略（利得を最大にする戦略）になるので、果たしてナッシュ均衡戦略\((p=1/2)\)を選ぶインセンティブがあるのか？という問題が起こります。これを論じたハルサニのpurification theoremという定理があります。これは完備情報の混合戦略ナッシュ均衡は、不完備情報の純粋戦略ナッシュ均衡の極限として表現できるという定理ですが、ここでは触れていません。
参考文献
- Harsanyi, J.C. Games with randomly disturbed payoffs: A new rationale for mixed-strategy equilibrium points. Int J Game Theory 2, 1–23 (1973). https://doi.org/10.1007/BF01737554
東京都立大学 2020ゲーム理論１ オンライン講義（2020：コロナ対応）
ゲーム理論における混合戦略
ここでは混合戦略とは何か、混合戦略のナッシュ均衡とは何かについて記していきます。計算方法は、ここではありません。必要ならば、以下も参照してみて下さい。
- 混合戦略ナッシュ均衡の求め方（簡略版）
- ２☓２ゲームの混合戦略のナッシュ均衡の計算方法について記しています。
- ナッシュ均衡の求め方：2人ゲームの利得行列の場合
- ２人ゲームでの混合戦略ではない純粋戦略のナッシュ均衡の求め方について記しています。略
- ナッシュ均衡（ざっくりした説明）
- ナッシュ均衡とは何かについて、ざっくり記しています。
- グリコ・チョコレート・パイナップルゲームの解
ナッシュ均衡のないゲーム？
戦略形ゲームの解であるナッシュ均衡について、その考え方と2人ゲームでの求め方について書きました。しかし2人の「じゃんけん」に対してナッシュ均衡を求めると、ナッシュ均衡が存在しないように見えます。
ナッシュ均衡は「お互いが利得を最大にしている戦略の組」です。じゃんけんでは「相手がグーなら自分はパーが良い（利得を最大にする）」「自分がパーなら、相手はチョキが良い」「相手がチョキなら自分はグーが…」と循環してしまい、お互いが利得を最大にしている戦略の組はないことが分かります。（循環するからダメなわけではないんですけど、正確には…）
確認するために、ナッシュ均衡の求め方にしたがい最適反応戦略（利得を最大にする戦略）となる利得に下線を引くと以下の図になり、両プレイヤーの利得に共に下線が引かれている戦略の組はないことが分かります。
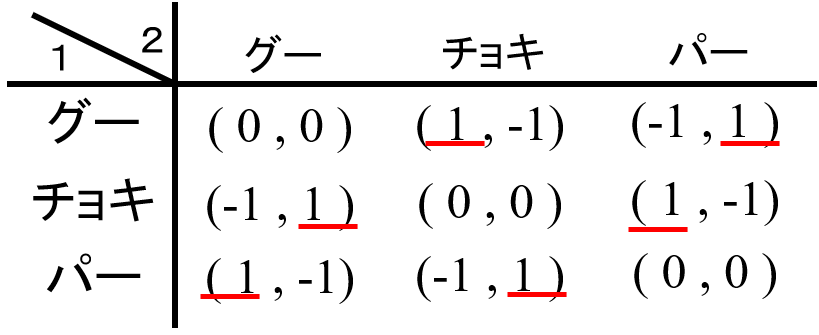
じゃんけんには戦略が３つありますが、戦略が２つであってもこのような（一見すると）ナッシュ均衡がないゲームはあります。以下のゲームは、その典型例として、よく用いられます。
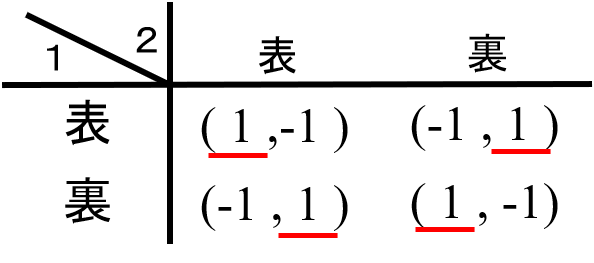
（マッチングペニー）2人のプレイヤーAとBが、それぞれ表(Head)か裏（Tail）を選ぶ。2人が同じものを選べばAの勝ち、違うものを選べばBの勝ち。
このゲームは「1セント硬貨（ペニー）をお互いに持ち、同時に表か裏かを出す」というゲームから由来していることから、マッチングペニー（matching pennies。 penniesって複数形なんだ…)と呼ばれています。
脱線しますが、日本人だと2人で順番を決めたり、勝ち負けを決めたりするときはじゃんけんをします。あっち（欧米）だとじゃんけんがなく、そのような状況では「表か裏を選ぶ」という方法を考えるのが定番のようで、ゲーム理論をやっていると頻繁に「表」「裏」を選ぶという状況が登場します。マッチングペニーが実際に行われているかどうか、私は知らないのですが（誰か教えて下さい）、テニスの試合なんかだと最初にサーブを取るかコートを選ぶかを決めるときに、一方の選手がラケットを地面に立ててぐるぐる回して放し、もう一方が落ちるラケットの上面が表か裏かを言い当てるという方法を使います（私のようなド素人だと、ラケットの表と裏が分からなくて、そこでつまづきます）。マッチングペニーに近いですが、ラケットを回すほうは自分の意志で表か裏を選択しているわけではないので「ゲーム」ではないですね。ちなみにテニスの大きな試合（ サッカー・アメフトなんかもそう）では審判がコイントスをして決めますが、これも第3者が決めているので「ゲーム」ではありません。くじと一緒です。
マッチングペニーでは、出したコインの表と裏が一致したときに、勝つプレイヤーと負けるプレイヤーをあらかじめ決めておく必要があります。これはマッチングペニーのルールがプレイヤーに対して非対称であることによります。ワタナベじゃんけんも同じで、どのような場合に誰が勝つかという、結果とプレイヤーを予め結びつけておく必要があります。戦略が２つだと対称で等確率に勝負がつくゲームは作れないのです。じゃんけんは、どのプレイヤーも勝ちの場合と負ける場合のルールが対称になっているゲーム（対称ゲーム）で、あらかじめ結果と勝者とを結びつけておく必要がありません。しかし戦略が３つ必要になります。どちらが好みでしょうか。日本人の私はじゃんけんのほうが好きですが（ラケットやペニーのような「道具」も必要なく、最初にどのようなときに誰が勝つかというプレイヤーを特定する必要もない）。じゃんけんは「あいこ」があるため勝負に時間がかかることがあります。戦略の数、必要とする道具、対称性、あいこと勝負の決定性、などを考慮するとどちらが良いかは好みで分かれるでしょう。
混合戦略
脱線してしまいましたが話を元に戻すと、マッチングペニーもじゃんけんと同様にナッシュ均衡がないように見えます。このような一見すると均衡がないゲームも、プレイヤーが確率を使って戦略や行動を選択すると考えるとナッシュ均衡が存在します。これはゲーム理論の出発点とも言える部分で、歴史的にはゲーム理論のキモと言うか核と言うか、そんな考え方なんです。
ゲーム理論では、プレイヤーが確率を用いて行動や戦略を選択することを１つの戦略とみなし、それを混合戦略(mixed strategy)と呼びます。もともと考えていた戦略を混合戦略と区別したいときは純粋戦略（pure strategy)と呼びます。純粋戦略は、確率１でそれを選ぶ混合戦略と同じと考えられるため、混合戦略は純粋戦略を含んだ考え方であると言えます（混合戦略は純粋戦略の拡張と言う方が数学的には正しいかな）。
「確率で戦略や行動を選ぶ」と言うと、「難しそうだ」「実際にそんなことあるのか」と言われそうですが、じゃんけんだと各プレイヤーが「グー・チョキ・パーを1/3ずつで選ぶ」というのが混合戦略のナッシュ均衡になります。マッチングペニーだと各プレイヤーが「表と裏を1/2ずつ選ぶ」というのがナッシュ均衡となります。そう考えると「確かに確率的に戦略を選ぶという考え方は分からないでもないな…」と思いませんか？
しかし、この混合戦略とナッシュ均衡の考え方は、なかなかの曲者で、正しく理解しにくいのです。以下では、これについて話していきます。
等確率でない場合
「確率で選ぶ」ということは「等確率で選ぶ」ことと同じではありません。以下の例を考えてみましょう。
（サッカーのPK戦のゲーム）サッカーのPK戦を簡便にしたモデルを考える。 キッカーは（キーパーから見て）ボールを左か右かのどちらかに蹴り、 キーパーは（自分から見て）左か右に飛んでゴールを阻止するとする（以下の図）。
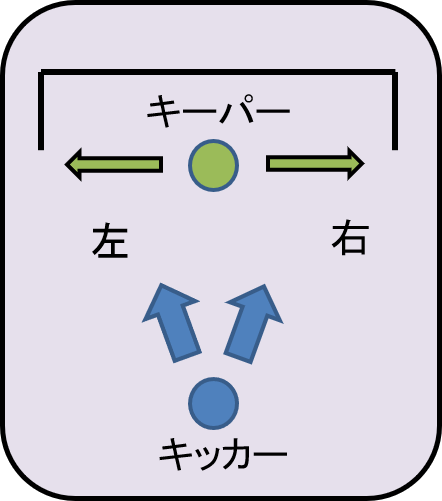
これをお互いが同時に右か左かを選ぶ戦略形ゲームと考える。 キッカーとキーパーは、違う方向に飛べばゴールの成功率は高く、同じ方向に飛べば低くなる。またキッカーは左に蹴る方が得意であり、 左のほうが成功率が高い。キッカーの利得は、ゴールの成功率、キーパーの利得は失敗率（１からゴールの成功率を引いたもの）とし、各成功率は以下のような利得行列で与えられているとする。
このようなゲームの解はどうなるだろう？
このゲームもナッシュ均衡を求めてみると、やはり（純粋戦略の）ナッシュ均衡はないことが分かります。そこで混合戦略のナッシュ均衡を求めると、
キッカーは右を5/8、左を3/8で選び、キーパーは右を7/8、左を1/8で選ぶ
となります。キッカーもキーパーも右と左を等確率で選ぶわけではありません。
どうやってこれを求めるのか？混合戦略のナッシュ均衡を求めることは、ゲーム理論の試験問題の定番です。いろんな大学のゲーム理論の講義の宿題や試験、さらには公務員試験などで出題されていて、ここを訪れた皆さんならやったことがあるか、もしくはそれを知りたくてここに来たのかもしれません。求め方は大切ですし、面白いのですけど、それは別に記すことにしましょう。
このページでは求め方ではなく、考え方について記していきますが、その前に、まず１つ重要な事実をお伝えします。上記のように一見するとナッシュ均衡がないように見えるじゃんけん、マッチングペニー、サッカーのPK問題でも混合戦略というものを考えるとナッシュ均衡がありました。実は
プレイヤーが何人いても、戦略がいくつあっても、混合戦略まで考えれば必ずナッシュ均衡は存在する
という数学の定理があるのです。凄い！凄すぎる！ナッシュ均衡は必ずあるんです（←ジョン・カビラさん風に読んで下さい、川平慈英さんでも可！）。これはゲーム理論において、たぶんいちばん重要な定理です。
この定理を証明した人は誰でしょう？賢明なあなたなら、それはもうお分かりだと思います。その人は、その功績を認められて1994年にノーベル経済学賞を取りました。
混合戦略のナッシュ均衡とは何なのか？
さてここでは求め方ではなく、上で求めた確率は「いったい何なんなのか？何の意味があるのか？」ということについて述べてみます。
専門家は、これについてハルサニーのpurification theorem(Harsanyi(1973))を考えると思いますが、ここではもう少し初心者向けの話をしてみます。
「何なんだと言われても、ナッシュ均衡でしょ？としか言いようがない！」というかもしれません。それでは以下の考え方は正しいでしょうか？
- （疑問１）キッカーは右を5/8、左を3/8で選ぶことが最適で、これに従うことが一番良いのだろうか？もし実際に自分が上のようなゲームに直面し、キッカーだったら、右を5/8で蹴ると一番良いのだろうか？
この「混合戦略のナッシュ均衡の戦略はゲームの必勝戦略で、それを出すことがプレイヤーにとっては一番いいんだ！」という考え方は正しいのでしょうか？
また、必勝戦略であるかどうかの前に、
- （疑問２）もしあなたがキッカーで5/8の確率で右に3/8の確率で蹴ろうとすると、どうやってボールを蹴るのだろうか？
という疑問もあります。疑問２は専門家には簡単なことなのでしょうが、学生に投げかけてみると、ほとんど答えられないようです。疑問１くらいだとさっぱり分かりません。
混合戦略のナッシュ均衡は求められるのに、それが何なのか分かっていないことが多い人が何と多いことか。私も成績をつける都合で宿題や試験に出しているんだということを正直に告白しなければなりません。 教員は、それに何の意味があるのか分かっていないものを、学生に求めさせていることを大いに反省しなければなりません。はい、いつか話そうと思っていました。なので、今回のこの記事は、スゴーク長くなっているのです。
まず疑問２について答えてみます。混合戦略は「確率で戦略を決定する」のですから、忠実に再現するには、何らかの「くじ」や「サイコロ」のような確率を発生させる仕組みが必要です。ゲーム理論の専門家は、これをランダムデバイス（random device）と呼びます。もし「右を5/6、左を1/6で選べ」と言われたら、「サイコロを振って1の目が出たら左、それ以外は右」を選びます。では「右を5/8、左を3/8で選べ」だと、どうすれば良いのでしょうか？このページの最後に答を記すので、皆さんで考えてみて下さい。
混合戦略のナッシュ均衡は必勝法か？
さていよいよ疑問１の「現実にゲームに直面したときに、混合戦略のナッシュ均衡に従うことは自分にとって最適なのか」ということについて考えてみます。実はこれはよく分からないんです。状況は零和ゲームか、非零和ゲームかで変わってきます。しかし私は「ざっくり言うと、必ずしもそうではない」と考えています。
それはまずじゃんけんについて考えると、分かりやすくなります。
２人じゃんけんのナッシュ均衡の戦略は「グー・チョキ・パーを1/3ずつ出す」という戦略になります。お互いに、この戦略を選んでいると、勝ち・負け・引き分けの確率は共にに1/3となります。
では仮に相手が「グーしか出さないやつ」で、そしてそれをあなたが知っていたら、あなたはどうします？このときはパーを出すことが最適です。当たり前です。そして、そうすれば、あなたは100％勝つことができます。しかし、もしあなたがナッシュ均衡の戦略である「グー・チョキ・パーを1/3ずつ出す」という戦略を選ぶとどうなるでしょう。このとき、あなたの勝つ確率は1/3になってしまいます。相手がグーしか出さないやつなのに、 あなたと相手の勝つ確率は、同じになってしまいます！
じゃんけんにおいて「グー・チョキ・パーを1/3ずつ出す」ということは最適戦略ではありません。これはナッシュ均衡の戦略でしかないのです。よくナッシュ均衡の戦略を「最適戦略」と書いている文章を見かけますが（学会発表などでもよく見られます…実は自分もそう書いてしまうことがあるのですが）、「最適」という言葉は相手の戦略が所与の場合でしか使えません。最適戦略と書かないで下さい、均衡の戦略と書いて下さい。
で？結局のところ「何なんだと言われても、ナッシュ均衡でしょ？としか言いようがない」っという所に戻って来てしまいます。つまり「混合戦略のナッシュ均衡は何を意味しているか」という問題は、そもそもの「ナッシュ均衡とは何か」という問題に立ち返ることになります。
ゲーム理論のナッシュ均衡には、いくつかの解釈があります。１つ目は「合理的なプレイヤーが、お互いがよく考えて行動を選択するとナッシュ均衡になるだろう」という考え方（伝統的なゲーム理論、合理的プレイヤーのゲーム理論）、2つ目は「プレイヤーの中で高い利得を獲得したプレイヤーだけが生き残り、そうでないプレイヤーが淘汰されるような環境で生き残っていく戦略はナッシュ均衡になるだろう」という考え方（進化ゲーム的解釈）。他に「第3者がプレイヤーにそれを推薦すると、プレイヤーはそれを選ぶだろう。それによって第3者は、自分やプレイヤー達を良い結果に導くことができる、と言う考え方もあると思いますが（メカニズムデザインなど）、あまり中心的ではないので、ここでは1つ目と2つ目の考え方に立ってみます。
１つ目と２つ目の の立場に立っても、ナッシュ均衡の戦略とは「あなたはそうすると良い、これが必勝法だ」というよりは、むしろ「プレイヤーは達はそう行動するだろうという予測」を述べているのに近いはずです。
混合戦略は確率的に行動を選択する戦略なので「プレイヤーは達はそう行動するだろうという予測」 と言っても、 1回のゲームの結果では当たっているかどうかは分かりません。サイコロで1の目が出る確率は1/6ですが、１回だけサイコロを振って出た目を見ても、その予測が正しいかどうか分からないのと同じことですよね。しかし何回も同じようなゲームが試行された場合、ナッシュ均衡の予測が当たっているかどうかを検証することができます。これについては
- 実験経済学における混合戦略の実験
- テニスやサッカーなどのスポーツの試合における実証
などがあり、いずれも混合戦略による予測は、それほど悪くはないという結果が導かれています。
まとめ
うーんかなり疲れてきたので、このへんで終わりにします。まとめると
- ナッシュ均衡がないように見えるゲームも、混合戦略のナッシュ均衡がある。必ずある。それを証明したすごい人がいる。
- 混合戦略のナッシュ均衡は最適戦略ではない。あくまでも均衡である。
- ナッシュ均衡は「そのようにプレイすることが良い」とは必ずしも言っておらず（注）、「人々はナッシュ均衡のようにプレイするだろう」と言っている。
そうは言ってもゲームにおいて「勝つために混合戦略のナッシュ均衡をうまく活用」する方法はあるはずです。 これについては、また別の機会に考えてみます。
混合戦略については、どのゲーム理論のテキストにも載っていますが、それが一体何なんだということについて書いてある本は、ほとんどないように見えます。この混合戦略のナッシュ均衡の解釈はかなり難しいからです。しかし東大の神取道宏先生は、一般向けの本などで（例えば神取（2014））このことについて言及されていて、さすがだなーと思います。
なお3/8で右、5/8で左に蹴るには、コインを3枚投げて、1枚だけ表が出たら右、それ以外（2枚表が出るか、全部表が出るか、全部裏が出る）だったら左に蹴るというのが正解です。「8本のあみだくじを引く」「八面体のサイコロを使う」なども正解でしょう。
注意点
ゲーム理論の研究者間だと混合戦略のナッシュ均衡は「ゲームの情報に僅かに不完備性があるゲームの純粋戦略均衡を考え、その不完備性がゼロに近づいたときの極限における均衡」と考えることもあります(Harsanyi (1973))。初心者向けのここではそれについては触れませんでした。
参考文献
- 神取道宏 (2014)、ミクロ経済学の力、日本評論社。
- Harsanyi, J. C.(1973) Games with randomly disturbed payoffs: A new rationale for mixed-strategy equilibrium points. Int J Game Theory 2, 1–23 . https://doi.org/10.1007/BF01737554
東京都立大学 2020ゲーム理論１ オンライン講義（2020：コロナ対応）
チキンゲーム
チキンゲーム(chicken game)は、2人のプレイヤーがそれぞれ「強気(Bull)」と「弱気(chicken)」のどちらかを選び
(1)相手が「弱気」なら、自分は「強気」の方が「弱気」より良い
(2)しかし両方が「強気」を選ぶと、2人にとって最悪な結果となる
というゲームです。
チキンゲームの例
以下の例を考えてみます。
（チキンゲームの例）2人のプレイヤー１と２はこれから共同でプロジェクトを行う予定であり、契約の前に獲得予定の利益100万円の分配について交渉をしている。2人はそれぞれ「強硬」か「妥協」のどちらかを選ぶ。両方が妥協すれば50万円ずつ折半となるが、一方が「強硬」に出て一方が「妥協」すると、強硬に出た方は75万、妥協した方は25万と利益を分ける。両方が強硬に出ると交渉は決裂してプロジェクトは行われず、双方の利益は0になる。
この状況を利得行列にすると、以下のようになります。
この状況では、各プレイヤー（１と２）はそれぞれ
(1)相手が妥協を選ぶなら、自分は妥協より強硬が良い
(2)両方が強硬を選ぶなら二人にとって最悪な結果となる
ことが分かります。これがチキンゲームです。
チキンゲームの解
チキンゲームの条件(2)は以下の(2*)と(3)ように書き直せるため、チキンゲームは以下の3条件に書き直すことができます。
(1)相手が「弱気」なら、自分は「強気」のほうが「弱気」より良い
(2*)相手が「強気」なら、自分は「弱気」のほうが「強気」より良い
(3)両方が「強気」より、両方が「弱気」のほうが２人にとって良い
(1)と(2*)からこのゲームの解（ナッシュ均衡）は、
一方のプレイヤーが「強気」を選び、一方のプレイヤーが「弱気」を選ぶ
であることが分かります。上述の100万円を分ける交渉の例だと
（A)プレイヤー１が「強気」、プレイヤー２が「弱気」を選ぶ
（B)プレイヤー１が「弱気」、プレイヤー２が「強気」を選ぶ
という２つの解が存在します（実は他に確率で選択を行う混合戦略のナッシュ均衡が１つある）。実際にナッシュ均衡の求め方に従って、利得に下線を引くと以下の図となり、両プレイヤーの利得に下線が引いてある戦略の組は、上記の(A)と(B)であることが分かります。
この（A)と（B)のナッシュ均衡のどちらが解になるのか、という問題は調整ゲームと同じで難しい問題です。調整ゲームと同じように、それまでの慣習などで「フォーカルポイント」が存在すればそれが解になりえますが、そのようなものがない場合はナッシュ均衡が実現するかどうかも難しい可能性があります。（調整ゲームとの関連は後述）
囚人のジレンマと間違えないで！
よくチキンゲームと囚人ジレンマは混同されます。上記の条件(1)(2*)(3)を見ると、(1)と(3)は囚人のジレンマと同じです。囚人のジレンマを
相手が協力するならば、自分は協力しない方が良い。しかし2人が共に協力しないよりは、2人が共に協力したほうが良い。
とだけ説明すると、これは囚人のジレンマか、チキンゲームか分かりません（相手が協力しないときに、自分は協力したほうが良いのか、協力しないほうが良いのかが分からないですよ）。囚人のジレンマと混同しないように注意しましょう。
調整ゲームとの関連は？
既に見たようにチキンゲームは調整ゲームと同じ構造を持っているようにも見えます。上述の100万円を分ける交渉において、各プレイヤーはAかBの「ラベル」を選ぶこととし、プレイヤー１はAならば「強気」をBならば「弱気」を選ぶことを意味しているとし、プレイヤー2はAならば「弱気」をBならば「強気」を選ぶことを意味しているとし、ゲームを置き換えるとしましょう。このゲームは以下のような利得行列に書き換えることができます。
このゲームは、相手と同じものを選んだほうが良い「調整ゲーム」であることが分かります。チキンゲームはこのように「2人だけの」「1回だけの」ゲームだと考えれば広義の調整ゲームであるとみなすことができ、分析上は区別する必要はありません。
しかしゲーム理論においては、
＊多人数のプレイヤーがいて、各プレイヤーは「強気」か「弱気」のどちらかを選ぶようなプレイヤーであるとする（戦略がある程度「固定」されている）。
＊それらのプレイヤーが、2人ずつ出会ってゲームを行う
＊プレイヤーの戦略は「進化」や「学習」によって更新される
と考える文脈（進化と学習のゲーム理論）もあります。この枠組みでは、上記のラベルの入れ替えはできません。この文脈では、チキンゲームと調整ゲームは異なるものと考えられます。実際に多くの進化や学習のゲームでは、調整ゲームはすべてのプレイヤーが同じ行動を選ぶ(上述のAとBを選ぶゲームでは全員がAを選ぶか、全員がBを選ぶかという結果になる）ことが解になるのに対し、チキンゲームはプレイヤーが棲み分けを行う（上述のチキンゲームでは、強気と弱気を選ぶプレイヤーが50%ずつに分かれる）ことが解になります。
このような進化や学習のようなモデルでは、チキンゲームは調整ゲームよりはむしろ混雑ゲームと似た構造になっていると考えられます。
東京都立大学 2020ゲーム理論１ オンライン講義（2020：コロナ対応）
調整ゲーム
調整ゲームはコーディネーションゲーム（coordination game）の翻訳で、協調ゲームと訳されることもあります。ざっくり言うと「他人と同じ行動を選ぶことが良い」ようなゲームです。結果となるナッシュ均衡は「全員が同じ行動を選ぶ」となるので（確率を用いる混合戦略を除く）、結果の候補が複数あることになります（複数均衡）。
女と男の戦い
ゲーム理論で最初に習う2人調整ゲームは、 以下のストーリーで表される女と男の戦い（battle of sexes）です（変な名前！でも昔は「両性の戦い」と訳されていました。これだとさらに意味不明です）。
アリスと文太は、禅寺かショッピングセンターに行く。2人は相手の行動を知らずに、どちらに行くかを選ぶ。アリスと文太は、お互いが好意を抱いているので同じ場所を選べば利得1を獲得し、さらにそれが自分が好きな場所ならば利得にもう1点が加わり2になる。違う場所を選んでしまうと（たとえ好きな場所に行ったとしても）利得は0である。
「女と男がいて、お互い同じ場所に行きたい。できれば自分の行きたいところがいい！」というそれだけのゲームです。男女が武闘しているわけではありません。この状況を利得行列にすると、以下のようになります。
この状況では、各プレイヤー（アリスと文太）はそれぞれ
(1)相手が禅を選ぶなら自分も禅を選ぶほうが良く
(2)相手がショッピングを選ぶなら、自分もショッピングを選んだほうが良い
となり、「相手と同じ行動を選ぶことが良い」となります。これが調整ゲームです。
調整ゲームの例
- どのSNSに参加するか、という問題。自分の友人が皆んなFaceBookを選んでいるならばFBを、インスタグラムを選んでいるならインスタを選ぶことが良い。このように商品に正の外部性（自分が購入する財から得る効用は、他の消費者がそれを多く選んでいるほど高くなる）があるときの消費者の選択は調整ゲームになります。
- 技術規格のデファクトスタンダード問題。かつてビデオデッキの開発において、各企業はVHS方式とベータ方式のどちらの規格を選ぶかという問題に直面しました。企業の選択は、多くの企業が選択するものと同じ規格を選択したほうが有利になります（wikipedia デファクトスタンダード）
- 同窓会の参加。皆んなが参加するならば、自分も参加したほうが良いけど、皆んなが参加しないなら、自分も参加しないほうが良い。
- 右側通行か左側通行か。細い道を車ですれ違うとき、右に避けるか左に避けるか。お互いに右か左か同じルールを選ばないと衝突してしまう。
調整ゲームのバリエーション
先ほどの「女と男の戦い」では、相手と同じ行動を選ぶことが良いわけですが、各プレイヤーは、どの結果が最良であるかが異なっています。アリスにとっては2人が禅を選ぶことが、文太には2人がショッピングを選ぶことが良いわけです。このような調整ゲームは非対称(asymmetric）であると言われます。これに対して「どの結果でも、2人が会えさえすれば同じ（1点）」のように、結果に差がなく、行動が一致さえすれば良いゲームは対称(symmetric)な調整ゲーム、純粋調整ゲーム(pure coordination game)、またはマッチングゲーム(matching game)と呼ばれます(Camerar 2003)。
2人とも買い物が好きで、禅寺で会えれば１点、ショッピング・センターで会えれば２点、のようなゲームも考えられます。このゲームでは、行動が一致しないより一致したほうが良いのですが、一致したときに皆にとって利得が高い場合と低い場合があります。このようなゲームには、定着した呼び名はありません。ここではTremblay and Horton(2012)に従いパレート調整ゲーム(Pareto coordination game)と呼んでおきます。
調整ゲームの解
調整ゲームでは、すべてのプレイヤーが同じ行動を選択することがゲームの解であるナッシュ均衡になります（他に確率を用いて選択を行う混合戦略のナッシュ均衡もあります）。例えば上述の女と男の戦いでは
(A)アリスも文太も禅寺に行く
(B)アリスも文太もショッピングに行く
という２つのナッシュ均衡があります（他に混合戦略のナッシュ均衡がある⇒最後の「注意点」を参照せよ）。実際にナッシュ均衡の求め方にしたがって利得に下線を引くと以下の図となり、両プレイヤーの利得に下線が引いてある戦略の組は、上記の(A)と(B)であることが分かります。
このように調整ゲームでは複数のナッシュ均衡が存在し、その中でどれを起こりうる結果である「ゲームの解」とするのか、という問題が起きます。この問題は均衡選択の問題と呼ばれ、ゲーム理論の大きな研究テーマです。
このときその中の１つのナッシュ均衡が起きるとすべてのプレイヤーが共通な認識で予測できるような理由があるならば、それは解となりえます。このような皆が共通して結果として予測できるような点はフォーカルポイントと呼ばれます（Schelling (1960)）。フォーカルポイントは、「社会慣習」や「これまで繰り返しプレイされてきて培われた経験」などによって形成されると言えます。
例えば上記の男と女の戦いでは、２人はいつも禅に行くことになっている（という慣習や経験があれば、２人は迷うことなく禅を選ぶでしょう。また、そのような経験がなくても「レディファースト」 （アリスに文太が譲る）という慣習があれば、やはり２人は禅を選ぶことになります。文太は、本当は２人でショッピングに行ったほうが良いのですが、アリスが禅に行くと予測するなら、ショッピングよりは禅が良い選択であり、アリスも文太が禅に行くと予測できるなら禅に行くことが良い選択です。つまりナッシュ均衡の定義である 「相手がそのナッシュ均衡の行動を選ぶなら、自分もそのナッシュ均衡の行動を選ぶことが一番良い」という条件を満たすことになります。
これに対して、上記のように２人が共通して予測できるフォーカルポイントがなければ、ナッシュ均衡は実現できるとは限りません。上記のようなゲームを実験室でやらせるとお互いが異なる行動を選び0点を食らってしまう結果も多く見られます。私も講義中にこの実験をやらせてみますが、うまくコーディネイトできるときもあれば、そうでない場合も多いです。うまくコーディネイトできない場合には、（当然ですが） 次の２つのパターンがあります：
・お互いに、自分が高い得点（2点）を選び合ってしまう。アリスが禅を、文太がショッピングを選び、お互いに0点を食らってしまう。
・お互いに、相手に高い得点を取らせようと譲ってしまう。アリスがショッピングを、文太が禅を選び、お互いに0点を食らってしまう。（私は「賢者の贈り物」パターンと呼んでいます。）
パレート調整ゲームでは、一般的にはプレイヤーにとって利得が高い<良い>ナッシュ均衡（パレート優位な均衡と呼ばれる） が望ましく、単純に考えるとそれが実現されると予想されますが、何らかの理由で両者にとって利得が低い＜悪い＞ナッシュ均衡が実現することも、十分あり得ます。先ほどの例２だと、２人ともショッピングに行くことで利得2が達成できるためこれが＜良い＞ナッシュ均衡ですが、例えば２人とも毎週毎週ずーっと禅寺に行っていることが定着していて、「相手は禅寺に行く」「相手は自分も禅寺に行くと予想するだろう」と考えれば(２人ともショッピングに行くほうが楽しいと分かっていても）禅寺に行くと考えられます。
調整ゲームにおいて、ナッシュ均衡が実現しない問題、ナッシュ均衡が実現してもパレート優位なナッシュ均衡が実現しない問題は、調整の失敗(coordination failure)と呼ばれます。
フォーカルポイントの例
単純なマッチングゲームでは、さまざまなフォーカルポイントがあると予想されますSchelling(1960)は、以下のようなゲームを（インフォーマルに）実験したようです。
- 表(head)か裏(tail)のどちらかを選べ。2人が同じものを選んだら賞金をあげよう。
- 好きな正の番号を選べ。2人が同じものを選んだら賞金をあげよう。
- ニューヨークのどこかで待ち合わせをする。どこで待ち合わせをするか選べ。
何を選んでも良いのですが、お互いに同じものを選ぶと良いので「調整ゲーム」であることが分かります。賞金に差もなく個人で選ぶと良いものに違いもないので、マッチングゲームですね。
Schelling(1960)によると最初のゲームでは42人中36人がheadを、2番めのゲームでは40%が「１」を選んだといいいます。3番めの質問では多数がGrand Central StationのInformation boothだとされています。
Mehta, Starmer and Sugden (1994)は、このような実験を精緻に行っています。この研究では被験者は２つのグループに分けられ、１つのグループC (Coordination)では「（ランダムに選ばれた）相手と同じものを選んだら賞金を与える」とされ、もう１つのグループP(Picking)では「何を選んでも賞金を与えるので、好きなものを選べ」としています。上記の最初の質問では、グループCでは87%、グループPでは76%がheadを選びそれほど差がないのに対して、2番めの質問では、グループCで選ばれたのは「１」が40%に選ばれて一番多く（「7」が2番めで14%）、グループPでは「７」が一番多く11%になっています。このことからある種の質問に対して、「自分が好きなもの」を選ぶのではなく「相手と同じものを選ぶためには何が良いか」を考えてそれを選ぶというフォーカルポイントが存在するということが分かります。
SchellingやMehta達は言及していないのですが、実験結果のデータを見て私が感じたのは「皆が同じものを選ぶと賞金をあげる」と言っているのに、自分が好きな数や場所を選ぶ被験者は、少数ながら必ずいるんだな…ということです。ルールが理解できていないのか、それとも何か意図があるのか.「フォーカルポイントに従う」という行動は、「大勢」や「傾向」ではありますが、それに逆らう（理解できない？従わない？）個の存在も無視できず、それはやはり「少数」や「個性」や「多様性」と言う社会科学の重要なテーマに繋がるのだな、と思いました。
注意点
- ここでは２人ゲームと多人数のゲームを曖昧に扱ってきましたが、厳密には分けて考えることが必要です。
- ここでは確率を使わない行動の選択（純粋戦略）のみを考えましたが、調整ゲームには各プレイヤーが確率を使って行動を選択する混合戦略を用いたナッシュ均衡もあります。例えば女と男の戦いの例だと「アリスは禅を2/3、ショッピングを1/3で選び、文太は禅を1/3、ショッピングを2/3で選ぶ」というナッシュ均衡があります。例１のマッチングゲームだと「アリスも文太も、禅とショッピングを1/2ずつ選ぶ」というナッシュ均衡があります。
- 相手と異なる行動を選ぶことが良いゲーム（チキンゲーム・混雑ゲーム）も広義の調整ゲームとみなされる場合があります。これはゲームの文脈を１回限りの２人のゲームと見做すか、多人数で長期間に渡って行われるゲームと考えるかで異なってきます。
- 調整ゲームにおいて「複数の均衡の中でどれが起きるか」という問題は、ゲーム理論における均衡選択という理論によって分析されており、リスク支配という概念によって起きる結果が選ばれます。
参考文献
- Camerar (2003), Behavioral Game Theory: Experiments in Strategic Interaction, Princeton Univercity Press.
- Mehta, Starmer, Sugden (1994), The nature of salience: An experimental investigation of pure coordination games, The American Economic Review, Vol.84, No.3, pp.658-673.
- Schelling(1960), The strategy of conflict, Harvard Univercity Press.
- Tremblay and Tremblay (2012), New Perspectives on Industrial Organization: With Contributions from Behavioral Economics and Game Theory, Springer.
以下も参考にしてください。
東京都立大学 2020ゲーム理論１ オンライン講義（2020：コロナ対応）
ナッシュ均衡の求め方：2人ゲームの利得行列の場合
ここではゲーム理論におけるナッシュ均衡を求める方法について。「プレイヤーが2人で混合戦略（確率を用いる戦略）を考えない場合」について説明します。ゲーム理論の基本中の基本と言えます。
ナッシュ均衡の求め方
ナッシュ均衡は「すべてのプレイヤーが最適反応戦略（利得が最も高くなる戦略）を選び合う戦略の組み合わせ」ですから、以下の方法で求めることができます。
- STEP1 プレイヤー１の立場で考える。
- 相手（プレイヤー２）のすべての戦略に対して、プレイヤー１がもっとも利得が高くなる戦略をチェックする（プレイヤー１の最適反応戦略）。ここでは利得に下線を引く。
- STEP2 プレイヤー１の立場でチェックが終わったら、プレイヤー２の立場で考える。
- 相手（プレイヤー１）のすべての戦略に対して、プレイヤー２がもっとも利得が高くなる戦略をチェックする（プレイヤー２の最適反応戦略）。ここでは利得に下線を引く。
- STEP3 すべてのチェックが終わったら、両プレイヤーの利得に下線が引かれているのがナッシュ均衡。（利得ではなく、戦略の組であることに注意！）
例題
以下の利得行列でナッシュ均衡を求めてみましょう。
今回は、ナッシュ均衡を求める手順を習得することが目的なので、ストーリーは特につけずに、単なる記号で利得行列を考えます。利得行列の読み方が不安、分からないって方は、こちらをご覧ください。
STEP1 まず、プレイヤー１の立場で考えます。相手（プレイヤー２）のすべての戦略に対して、プレイヤー１がもっとも利得が高くなる戦略（最適反応戦略）をチェックし、利得の下に下線を引いて行きます。
1.1 プレイヤー２がLという戦略を選んだ場合を考えます。プレイヤー１はTを選べば利得３、Bを選べば利得２です。したがってプレイヤー１はTを選びます（TがLに対する最適反応戦略）。そこでTを選んだ時の利得３に下線を引きます。
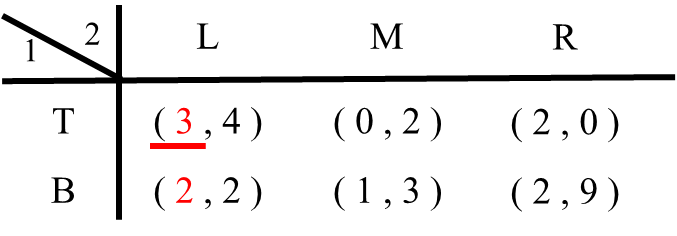
1.2 プレイヤー２がMという戦略を選んだら？プレイヤー１はTを選べば利得0、Bを選べば利得1です。したがってプレイヤー１はBを選びます（BがMに対する最適反応戦略）。そこでBの利得１に下線を引きます。
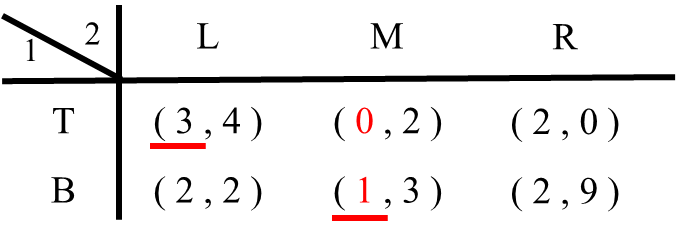
1.3 最後にプレイヤー２がRという戦略を選んだ場合を考えます。プレイヤー１はTを選んでも、Bを選んでも利得は２で同じです。この場合はTとBの利得２の両方に下線を引きます（ TもBもRに対する最適反応戦略）。
STEP2 プレイヤー１に対する検討が終わったので、次にプレイヤー２の立場で考えます。相手（プレイヤー１）のすべての戦略に対して、プレイヤー２の利得がもっとも高くなる戦略（最適反応戦略）をチェックし、利得に下線を引いて行きます。
2.1 プレイヤー１がTという戦略を選んだ場合を考えます。プレイヤー２はLを選べば利得４、Mを選べば利得２、Rを選べば利得０です。したがってプレイヤー２はLを選びます（LがTに対する最適反応戦略）。そこでLの利得４に下線を引きます。
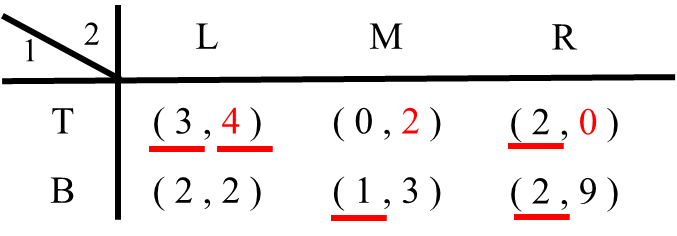
2.2 最後にプレイヤー１がBという戦略を選んだ場合を考えます。プレイヤー２はLを選べば利得２、Mを選べば利得３、Rを選べば利得９です。したがってプレイヤー２はRを選びます（RがBに対する最適反応戦略）。そこでRの利得９の下に線を引きます。
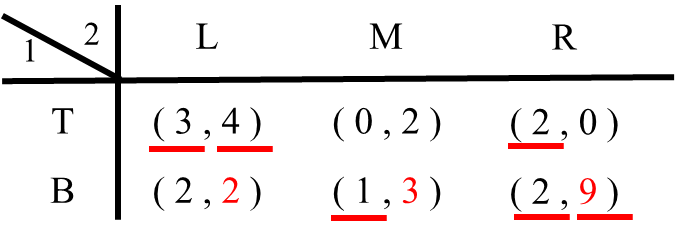
STEP３これでプレイヤー１とプレイヤー2のすべてのチェックが終わりました。プレイヤーの両方の利得に下線が引かれている戦略の組がナッシュ均衡です！「
ナッシュ均衡は「プレイヤー１はTを選び、プレイヤー２はLを選ぶ」「プレイヤー１はBを選び、プレイヤー２はRを選ぶ」の２つです。このようにナッシュ均衡は複数出てくる場合があります（これが悩みの種）。これを(T,L)と(B,R)のように、ベクトルのように書く場合もあります。
ナッシュ均衡は「戦略の組 (profile of strategies)」なので、戦略の組として答えます。「ナッシュ均衡は(3,4)と(2,9)です」などと答えては間違いです。それは利得の組ですから。「Tがナッシュ均衡」などと答えても間違いです。Tはプレイヤー１の戦略(a strategy of player 1）です。戦略の組み合わせではありません。
東京都立大学 2020ゲーム理論１ オンライン講義（2020：コロナ対応）
ナッシュ均衡（ざっくりした説明）
ここではまずナッシュ均衡について、ざっくり説明します。
ナッシュ均衡とは
ゲーム理論におけるナッシュ均衡とは、ざっくりいうと
どのプレイヤーも、自分だけでは、それ以上利得が大きくできない状態
です。「状態」って言い方は不正確過ぎるか。もう少し正確に言うと、ナッシュ均衡とは
どのプレイヤーも、他のプレイヤーがそのナッシュ均衡の戦略を選んでいるもとでは、その戦略が一番利得が高くなる（他の戦略では利得が同じか低くなる）
ような戦略の組です。あんまり変わんないか。
ナッシュ均衡の例
例を挙げましょう（これは支配戦略を説明するときに用いた例の「客数」を変えたものです）。
２つのコンビニ、セレブ（セレブイレブン）とファミモ（ファミリーモール）が、まだコンビニがないA駅とB駅のどちらか一方に出店しようと考えている。コンビニを１日に利用する客はA駅が600人、B駅が750人である。セレブとファミモがもし違う駅を選べば、利用客を独占できる。しかし同じ駅に出店すると、ファミモが人気で、ファミモはセレブの2倍の客数を獲得できる。すなわち両方がA駅に出店すると、セレブ200人、ファミモ400人。B駅に出店すると、セレブ250人、ファミモ500人である。ここで客数を利得と考える。セレブとファミモはどちらの駅に出店するだろうか？
このゲームを利得行列で書くと下のようになります
例えば「セレブとファミモが共にA駅を選ぶこと」はナッシュ均衡ではありません。なぜならセレブは、ファミモがA駅を選んでいるなら、B駅に変えたほうが利得が高くなるからです。このように、他のプレイヤーの戦略が変わらないもとで、あるプレイヤーが選択を変えると利得が高くなるならば、その戦略の組はナッシュ均衡ではありません。
これに対し、例えば「セレブがA駅、ファミモがB駅を選ぶこと」はナッシュ均衡です。なぜならセレブもファミモも、相手がそれを選んでいる限り、自分の利得をもっとも高くしているからです。つまりナッシュ均衡では、
どのプレイヤーも（相手がその戦略を選んでいるならば）、それ以上利得を高くできない （他の戦略では利得が同じか低くなる）
と言うことになります。
ナッシュ均衡は2つ以上あるときもある
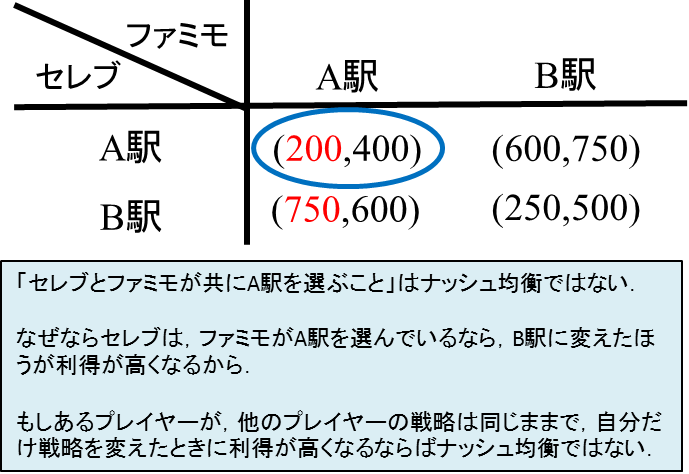
しかしこの例では「セレブがA駅、ファミモがB駅を選ぶこと」だけではなく、「セレブがB駅、ファミモがA駅を選ぶこと」 もナッシュ均衡になることが分かります。つまりナッシュ均衡は1つとは限らず、2つ以上ある場合もあります。このときどちらをゲーム理論の解とすべきかは難しい問題で、これは「均衡選択」と呼ばれる理論と「均衡精緻化」と呼ばれる理論で考えられています（2つの違いを説明するのはちょっと難しい）これはまた別の機会に。
ナッシュ均衡が複数あるゲームの代表例は、調整ゲームとチキンゲームです。調整ゲームの記事では、どういうときにナッシュ均衡が実現しやすいかについても述べています。
ナッシュ均衡がなぜ解なのか
ナッシュ均衡以外が結果として予測されたとします。このとき、もしすべてのプレイヤーがその予測を知ったならば、少なくとも1人はその予測から違う行動を取ることで利得を高くすることができるはずです。そのプレイヤーは、ナッシュ均衡と違う行動を取るでしょうから、もはやその予測は当たりません。このことから、ゲームの結果の予測をプレイヤーが知っても結果が成り立つためには、その予測はナッシュ均衡でなければならないはずです。（「じゃんけんの必勝法と行動ファイナンス・行動経済学」も参考にしてください）
注意点と補足
- すべてのプレイヤーが支配戦略を選んでいるときはナッシュ均衡になります。これはナッシュ均衡の特殊ケースと考えられます。したがって囚人のジレンマの結果もナッシュ均衡であると言えます。
- 上記の点から考えると、じゃんけんにはナッシュ均衡がありませんが、確率を用いる「混合戦略」を考えるとナッシュ均衡が存在します。このような混合戦略まで考えると、すべてのn人有限ゲームにナッシュ均衡が存在します。この素晴らしい定理を誰が証明したかは、よく考えれば分かるはずである。これによって、その人はノーベル経済学賞を受賞しています。私ではありません。
- ナッシュ均衡が分かったような気がしない？もう少し理解を深めたい？ではナッシュ均衡のおけいこ(1)で練習しましょう
- 2人ゲームの利得行列でのナッシュ均衡の求め方はこちら
- 混合戦略のナッシュ均衡の求め方
- クールノー均衡はこっち
東京都立大学 2020ゲーム理論１ オンライン講義（2020：コロナ対応）
囚人のジレンマ
囚人のジレンマとは
囚人のジレンマは、ゲーム理論の中で、もっとも有名な例・モデルと言えるでしょう。
２人のプレイヤーが「協力するか」「協力しないか」を選ぶ問題で、以下の3つの条件が成立するときに、それは囚人のジレンマと呼ばれます。
(1)各プレイヤーは、相手が協力するならば、自分は協力しないほうが良い。
(2)各プレイヤーは、相手が協力しなくても、自分は協力しないほうが良い。
(3)しかし各プレイヤーは、２人が協力しないよりは、２人が協力したほうが良い。
(1)と(2)から、相手が何を選んでも自分は「協力する」より「協力しない」ほうが良いので、2人は協力しないことを選択します。しかしその結果が2人が協力することよりも悪くなっているために問題となるわけです。
ここで 「協力する」ことはゲーム理論では支配戦略と呼ばれます。支配戦略は、相手が何を選んでも、自分にとって他の選択より良い選択です。このことから支配戦略を選ぶことは自明のように思えるのですが、 囚人のジレンマを考えると支配戦略を選ぶことが必ずしも自明では思えなくなります。
囚人のジレンマの由来
この問題が囚人のジレンマと呼ばれるのは、タッカー(A. Tucker。カルーッシュ・クーン・タッカー条件(Karush-Kuhn-Tucker condition)のタッカーです）という数学者が上の状況を以下のようなストーリーで表現したことが由来であると言われています（以下はタッカーのオリジナルのストーリーとは違います）。
（囚人ジレンマ ストーリー）重罪を犯しているが、証拠が不十分なため軽微な罪で逮捕されている２人の囚人がいる。彼らは別々な部屋で取引を持ちかけられる「お前だけが重罪について自白すれば無罪にしてやる」。
もし２人が黙秘を続けると、軽微な罪で懲役１年である。しかし１人が自白し、１人が黙秘をすると、自白した方は釈放、黙秘した方は（捜査に協力しないことで罪が重くなり）懲役10年。しかし両方が自白すると（重罪で）懲役5年になる。
さて、あなたが囚人ならば自白したほうが良いか、黙秘したほうが良いか？
この状況を表にすると、以下のようになります。
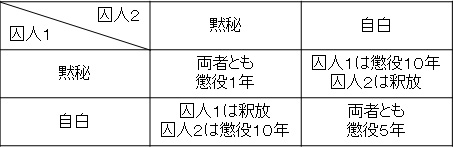
先に述べた「協力すること」を「黙秘」に、「協力しないこと」を「自白」に置き換えると、囚人のジレンマの３条件に当てはまることが分かります。すなわち、
(1)各囚人は、相手が黙秘するなら、自分は自白するほうが良い。
(2)各囚人は、相手が自白するとしても、自分は自白するほうが良い。
(3)しかし各囚人は、２人が自白するよりは、２人が黙秘したほうが良い。
相手が黙秘しても自白しても、自分は黙秘するより自白するほうが良いので、2人は自白を選びます。しかし、その結果は2人が黙秘するよりも悪くなります。
囚人のジレンマの例
この問題が興味を持たれるのは、社会や経済や政治の問題にこのジレンマが多く現れるからです。例えば
- 2国間の軍備拡張の問題。相手国が軍備拡張しない場合、自国だけが軍備拡張をすれば相手に外交上優位な立場に立てる。相手国が軍備拡張しない場合は、自分も拡張して追いつかなければ、相手に優位に立たれてしまう。しかし、両国とも拡張すると、拡張前と力のバランスは変わらず、ただ軍事費だけが増えてしまう（核兵器の問題にも同様な文脈が使われます）。
- 安売りの問題。競争関係にある2店舗が、顧客を取り合うために、商品の価格を現状維持とするか、安売りをするかの問題。相手が現状維持の場合、自分だけが安売りをすれば顧客を奪い売上が増えるので、安売りをしたほうが良い。相手が安売りをしている場合、自分だけが現状維持をすると顧客を奪われ売上が減少するので、こちらも安売りをしたほうが良い。しかし両者が安売りをすると、顧客を奪うことはできず、価格の低下で売上だけが減ってしまう。
と言った現象です。なお安売りの問題は、安売りをしている企業にとっては問題ですが、消費者にとってはそれ以上に恩恵があります。市場の価格競争は、囚人のジレンマという構造を利用して消費者の厚生を高める仕組みだと言うこともできます。
囚人のジレンマの繰り返し
囚人のジレンマは、本来なら協力することが望ましい2人が協力しない方が良いという結果になってしまうジレンマです。これは、協力することをコミットするような契約（協力しなければ罰金を払うなど）を結ぶことで解決できる可能性がありますが、国家間の関係のように、このような契約を結ぶことが難しい場合もあります。このような場合、囚人のジレンマの状況は1回きりではなく、長期間に継続する問題でもあります。このような長期間に続く囚人のジレンマは、囚人のジレンマを何度も繰り返すようなゲームだと考え、繰り返しゲームという枠組みで分析されます。
注意点
囚人のジレンマを語るには、以下のことに注意する必要があります。
- 2人ではなく3人以上の多人数版の囚人のジレンマは共有地の悲劇と呼ばれます。（3人以上でも、「囚人のジレンマ」と呼ばれることもありますが）。
- 「2人が協力しない」というゲームの解を支配戦略ではなく、ナッシュ均衡であるとしている解説もあります。全員が支配戦略を選ぶことは、ナッシュ均衡の特殊ケースなので、そうしても間違いではありません。しかしナッシュ均衡より強い支配戦略として理解するほうが適切です。
- 囚人のジレンマと言われている状況でも、3つの条件のうち、(2)について抜けている場合があります。例えば
X先生と2人で教授会で口論になり、教授会の時間がどんどん長引いている。(1′)X先生が折れるなら、自分は折れるより折れないほうがいい。(2′)自分が折れるなら、X先生は折れるより折れないほうがいい。(3′)でも２人が折れないなら、教授会は長引くばかりで、それなら2人とも折れたほうがいい（まったくの、まったくのフィクションです）。
一見すると条件が３つ揃ってるように見えますが、(1′)も(2′)も「相手が協力するなら、自分は協力しないほうが良い」という囚人のジレンマの条件(1)を２人のプレイヤーに分解して言い換えただけで、条件(2)（相手が折れないなら、自分は折れたほうが良いのか、折れないほうが良いのか）が特定されていません。もし「相手が折れないなら、自分は折れたほうがいい」ならば、これはチキンゲームです。
囚人のジレンマのブックガイド
- 囚人のジレンマ－－フォンノイマンとゲームの理論 (1995)、ウィリアム・パウンドストーン（著）、松浦俊輔（訳）、青土社、\2600、ISBN：4791753607。
- まさに「囚人のジレンマ」をタイトルにした本だが、それのみではなくゲーム理論の歴史と逸話に、ゲーム理論の初歩的な考え方を絡めた読み物である、ゲーム理論とは何かを知る入門書としても面白い。囚人のジレンマの誕生や囚人のジレンマに関する多くの研究について知ることができる。キューバ危機ではノイマン自身が原子力安全委員会の委員長として、ソ連とアメリカの囚人のジレンマにどう対応したかなどが興味深く記されている。原著はW. Poundstone、 Prisonaer’s Dillemma (1992)、Doubleday。
- つきあい方の科学―バクテリアから国際関係まで (1984)、R. アクセルロッド (著)、Robert Axelrod (原著)、松田 裕之 (翻訳)、Minerva21世紀ライブラリー（ミネルヴァ書房）、\2600、ISBN：4623029239。
- 「囚人のジレンマ」の研究の中で、一般の人に有名で影響が強く、分かりやすいのはロバート・アクセエルロッドのコンピュータプログラムどうしのトーナメントによる実験であろう。この本は、その詳細をな結果や経緯をもとに、囚人のジレンマ研究のビジネスへの応用が解かれている。
- 信頼の構造－－こころと社会の進化ゲーム (1998)、山岸敏男（著）、東京大学出版会、\3200、ISBN：413011086
- 社会心理学の立場から実験やゲーム理論の成果などをふまえて囚人のジレンマや社会的ジレンマがどのように起こり、どのように解決されるかの要因を探り、分かりやすく解説した本。馴れ合いや安易な集団主義に警告を発し、真の信頼関係を築くために何が必要なのかを語る。出版当時は、これからの日本がどうあるべきかを示唆すると共に実験経済学などの方面を踏まえて、これからのゲーム理論がどのように進むべきかも考えさせられた。
- 社会的ジレンマ－－環境破壊からいじめまで(2000)、山岸敏男（著）、PHP新書、\660、ISBN：4569611745
- 前述の本が社会的ジレンマ研究のサーベイや実験経過などを理論的に解説する研究者向けの本であるのに対して、同著者のこの本は社会的ジレンマとその解決を一般向けに解説した本であった。
- 対立と協調の科学－エージェント・ベース・モデルによる複雑系の解明 (2003)、ロバート・アクセルロッド (著)、寺野 隆雄 (翻訳)、ダイヤモンド社、\3800、ISBN：447819047X ロバート・アクセルロッド最新刊